| Geodesy | |
On the estimable parameters for selenodesy with space VLBI
In this paper, based on the SVLBI observations, the basic observation mathematical model for geodesy and selenodesy is introduced |
|
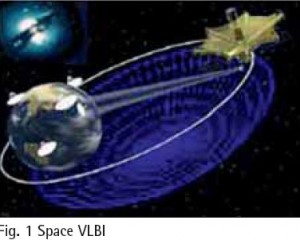
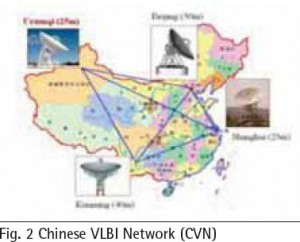
Space Very Long Baseline Interferometry (SVLBI) is an extension of the ground-based VLBI technology to space, which involves a simultaneous observation of the same radio source by two stations; one on the ground, the other being space-based. It could not only overcome the baseline length limitation problem specific to ground-based VLBI technology, with a great improvement on the observation resolution, but could also directly interconnect the important three reference systems (that is Terrestrial Reference System, Celestial Reference System, and the Dynamic Reference System). These advantages imply tremendous potential for SVLBI in space geodetic applications. The successful launch of Chang’e-I lunar probe makes it possible to place a VLBI antenna on the lunar probe some day to form ground-space VLBI observations. As an important component of the Chinese VLBI Network (CVN), Urumqi astronomical observatory will play an essential role. Based on all these factors, it is necessary for us to investigate the mathematical model with SVLBI observations in selenodesy studies.
Basic mathematical model
Coordinate system
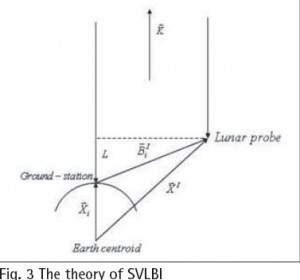
The orbit of lunar probe can be divided into phasing orbit, cislunar transfer orbit and circum-lunar orbit. According to the coordinate systems corresponding to different orbits, here we demonstrate the phasing orbit and cislunar transfer orbit as cislunar period, with earth satellites as its probe; and illustrate the lunar orbit as the circum-lunar period, with lunar satellites as its probe.
Coordinate systems corresponding to different periods
Cislunar period
Real space VLBI observation should be done under the Newton inertial coordinate system. Because of its independence from the self-rotation of the earth, the coordinate of every point on the earth under the inertial system varies with the earth’s rotation. In order to conveniently describe the position of ground stations, an earth-fixed coordinate system should be established depending on the technologies of GPS, etc, which could be named as Conventional Terrestrial System (CTS). In cislunar period, position of the ground VLBI station should be described under this system. Also, the lunar probe in the cislunar period serves as an earth satellite, therefore we could define both its dynamic equation and coordinates under the J2000.0 geocentric inertial coordinate system. Radio source direction vector is established based on FK5 star table under the J2000.0 heliocentric inertial coordinate system.
Circum-lunar period
In this period, ground VLBI station and radio source direction vector still refer to the earth-centered earth-fixed coordinate system and the J2000.0 heliocentric inertial coordinate system respectively. Coordinate of the lunar probe in this period has a close relation with the barycenter of the moon (that is lunar ephemeris), while planetary ephemeris of the solar system is given in the heliocentric ecliptic coordinate system, thus motion status of the interstellar probe away from earth should be discussed in this kind of system too. At present, the applied heliocentric ecliptic coordinate system refers to the J2000.0 heliocentric ecliptic coordinate system, with its basic plane and principle direction indicating the J2000.0 mean elliptic and mean equator respectively. Position of the lunar probe in the circum-lunar period could be demonstrated in this system. On the other hand, for convenience, chang’e-1 lunar orbiter still gives the coordinate of the lunar probe under the J2000.0 geocentric inertial coordinate system, which only has a translation amount with the selenocentric inertial coordinate system. Therefore, coordinate of the lunar probe could be also given in the selenocentric inertial coordinate system, whose definition is similar to the J2000.0 geocentric inertial coordinate system, and could be named as J2000.0 selenocentric inertial coordinate system.
Transformation between coordinate systems
Coordinate system transformation involves coordinate translation and rotation, among which the coordinate rotation is often realized by basic rotation matrixes as:












 |
|
|||||
 |
|
|||||
 |
|
|||||
My coordinates |
EDITORIAL |
|
Conference |
Where navigation meets the world, NRSC User Interaction Workshop 2010 |
|
News |
INDUSTRY | GPS | GALILEO UPDATE | LBS | GIS | REMOTE SENSING |
|
Mark your calendar |
APRIL 2010 TO NOVEMBER 2010 |


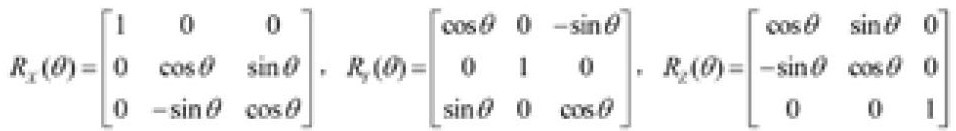











 (No Ratings Yet)
(No Ratings Yet)






Leave your response!