Contact | Previous Issues | Articles-by-Author

Improved algorithms for sailing calculations

May 2010 | No Comment

Numerical tests and comparisons

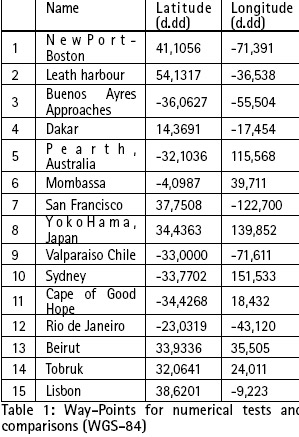
For the numerical evaluation of the proposed new algorithms for RLS and GES calculations, a data set of ten (10) routes between selected ports and harbors has been used (table 1).

These routes cover distances from 500 up to about 9000 nautical miles distributed all over the globe (figure 5).

The proposed new algorithm for RLS has been tested against:

• The simplified formulas for RLS on the sphere.

• The rhumbline sailing module of the Navpack navigational software, which is provided jointly by the UK Almanac office and the US Naval Observatory [12].

• Typical commercial ECDIS kernel navigational SW for RLS calculations.

The proposed new algorithm for GES [8] has been tested against:

• Other methods and formulas for GES that were proposed in the past as those of Williams[9] and Earle [13].

• Vicenty’s algorithm for the precise calculation of geodesic
distances and azimuths [8]

• Typical commercial ECDIS kernel navigational SW.

• Traditional G.C (Great Circle) sailing formulas on the sphere.

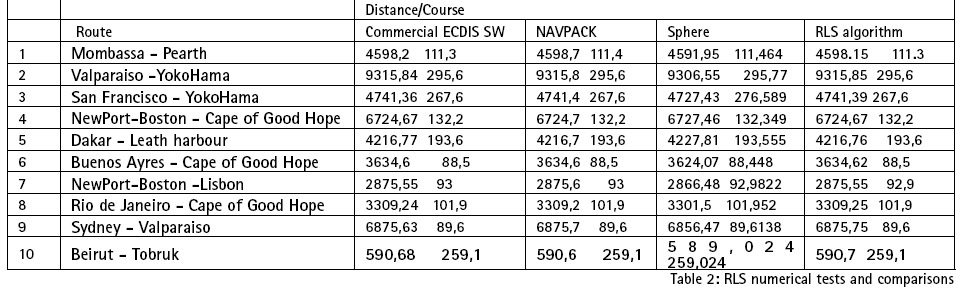
The conducted numerical tests(tables 2 and 3) show that:

• The average error of the proposed new algorithm for GES in the calculation of the great elliptic arc distances is 4,38 meters. This error is smaller than the 6,54 meters average errors of the methods of Williams and Earle. Seeking higher accuracy for sailing calculations does not have any practical value for marine navigation and simply adds more complexity to the calculations.

• Discrepancies in the computed distances between the “geodesic” and the “great elliptic arc” are practically negligible for marine navigation.

• Discrepancies between the results of shortest navigational path calculations on the spherical model of the earth as great circle arcs and on the ellipsoidal model as great elliptic arcs, or
geodesics, may in some cases exceed 15 nautical miles (~28.5 km).

• The discrepancies between RLS calculations on the sphere and the ellipsoid for very long sailing distances may exceed 19 nautical miles (~35 km).

• For short sailing distances (smaller than 600 nautical
miles) the discrepancies between the calculations on the spherical and the ellipsoidal model of the earth practically can be considered negligible for navigation.

Conclusions

The new improved algorithms for RLS and GES calculations:
• are straightforward and can be easily implemented in navigational software,
• provide the same and in some cases, higher accuracy than other
methods and formulas for sailing calculations on the ellipsoid,
• can be used in programmable pocket calculators for the solution of the inverse RLS and GES problems,
• are used for the calculation of the geodetic coordinates of an unlimited number of intermediate points along the rhumbline and the great elliptic arc and thus they can be easily implemented in navigational systems (ECDIS and ECS) for the display of navigational paths on the Electronic Chart Systems (ECDIS and ECS).
Detailed presentations of the improved algorithms for sailing calculations in GIS navigational systems can be found in references [3], [4] and [11].

Abbreviations
ECDIS: Electronic Chart Display and
Information System
ECS: Electronic Chart System
ENC: Electronic Navigational Chart
G.C: Great Circle
GES: Great Elliptic Sailing
RLS: RhumbLine Sailing

References

Bennet G.G. 1996. Practical Rhumb Line Calculations on the Spheroid. Journal of Navigation, Vol. 49 No 1. 112-119.

Earle M. A. 2006. Sphere to Spheroid Comparisons, Journal of Navigation, Vol.59, 491-496.

Pallikaris A. Tsoulos L. Paradisis D. New meridian arc formulas for sailing calculations in GIS, International Hydrographic Review May 2009.

Pallikaris, Α. Latsas, G. New algorithm for Great Elliptic Sailing (GES), Journal of Navigation, Vol. 62, No 3. 493-507.

Snyder, J. P. 1987. Map Projections: A Working Manual. U. S. Geological Survey Professional Paper 1395

Torge, W. 2001. Geodesy 3rd edition. Walter de Gruyter, Berlin, New York. Tobler. W.R. 1964. A comparison of spherical and ellipsoidal measures. The Professional Geographer, Vol XVI, no 4, pg 9-12.

Vincenty, T. 1975. Direct and Inverse Solutions of Geodesics on the Ellipsoid with Application of Nested Equations. Survey Review, vol. XXII no 176. 88-93.

Williams, R. 1996. The Great Ellipse on the surface of the spheroid. Journal of Navigation, Vol. 49, No 2. pp. 229-234.

Bowring, B.R. 1984. The Direct and Inverse Solutions for the Great Elliptic Line on the Reference Ellipsoid. Bull. Geodesique, 58 pp. 101-108.

Pallikaris A. Tsoulos L. Paradisis D. New calculation algorithms for GIS navigational systems and receivers, Proceedings of the European Navigational Conference ENCGNSS 2009. Naples Italy May 2009.

Hohenkerk C.Y. and Yallop B.D. 2004 NavPac and Compact Data 2006 – 2010 Astro-Navigation Methods and Software for the PC. TSO, London

Earle, M. A. 2000. A Vector Solution for Navigation on a Great Ellipse. Journal of Navigation, Vol. 53, no 03

Athanasios Pallikaris

Associate Professor, Hellenic Naval Academy

palikaris@snd.edu.gr

Lysandros Tsoulos

Professor,

National Technical University of Athens

lysandro@central.ntua.gr

Demitris Paradissis

Professor,

National Technical University of Athens

dempar@central.ntua.gr


	My Coordinates	EDITORIAL
	His Coordinates	Orhan Altan, President, ISPRS
	News	INDUSTRY \| GPS \| GALILEO UPDATE \| LBS \| GIS \| REMOTE SENSING
	Mark your calendar	MAY 2010 TO NOVEMBER 2010