| Navigation | |
Fuzzy strong tracking unscented Kalman filter
|
||||||||||||||||||||
| The Global Positioning System (GPS) (Brown and Hwang 1997; Farrell and Barth 1999; Gelb 1974) and inertial navigation system (INS) have complementary operational characteristics and the synergy of both systems has been widely explored. An integrated GPS/INS system is typically carried out through the extended Kalman filter (EKF). The EKF is the approximate nonlinear filters which linearizes the system and measurement equations about a single sample point with the assumption that the a priori distribution is Gaussian.
The EKF uses first order Taylor series expansion, which can be improved by higher order approximations at the expense of computational burden. The unscented Kalman filter (UKF) (Wan and van der Merwe 2000; Wan and van der Merwe 2001; Simon 2006) has been developed in the context of state estimation of dynamic systems as a nonlinear distribution (or densities in the continuous case) approximation method. The adaptive Kalman filter (AKF) (Mehra 1972; Mohamed and Schwarz 1999; Ding, et al. 2007; Hide, et al. 2003) has been one of the strategies to prevent divergence problem due to modeling errors. A relatively new adaptive filter proposed by Zhou and Frank (1996) is called the strong tracking Kalman filter (STKF), which has several important merits: (1) strong robustness against model uncertainties; (2) good real-time state tracking capability, no matter whether the system has reached steady state or not; (3) moderate computational load. In the same way, a filter called the strong tracking unscented Kalman filter (STUKF) is developed based on the combination of UKF and STKF, leading to the STUKF. The conventional approach for determining the softening factors relies on personal experience or computer simulation using a heuristic searching scheme. A new approach called the fuzzy strong tracking unscented Kalman filter (FSTUKF) is suggested. In the algorithm, the fuzzy logic reasoning system (FLAS) (Sasiadek, et al. 2000; Jwo and Lai 2009) based on the Takagi-Sugeno (T-S) model (Takagi and Sugeno 1985) is incorporated into the STUKF. The fuzzy reasoning system is constructed for obtaining suitable softening factors according to the time-varying change in dynamics. By monitoring the innovation information, the FLAS, as the filter’s internal mode, is employed for dynamically adjusting the softening factors based on the fuzzy rules so as to enhance the estimation accuracy and tracking capability. The proposed FSTUKF scheme is applied to the loosely-coupled GPS/INS navigation processing to improve the navigation estimation accuracy at the high dynamic regions while preserving/without sacrificing the precision at the lower dynamic regions. The performance of the proposed FSTUKF method is compared to those of the EKF, UKF, and STUKF approaches. The Unscented Kalman FilterThe nonlinear filters deal with the case governed by the nonlinear stochastic difference equations:
where the state vector xk∈ℜn, process noise vector wk∈ℜn, measurement vector zk∈ℜm, and measurement noise vector vk∈ℜm. The vectors wk and vk are zero mean Gaussian white sequences having zero crosscorrelation with each other:
The discrete-time extended Kalman filter algorithm is summarized:
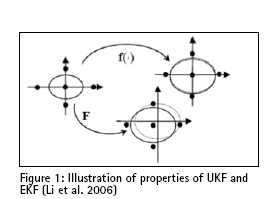
In the EKF, the state distribution is approximated by a Gaussian random variable (GRV), which is then propagated analytically through the first-order linearization of the nonlinear system. Wan and van der Merwe (2000) pointed out that this will introduce large errors in the true posterior mean and covariance of the transformed GRV and lead to suboptimal performance and sometimes filter divergence. The basic premise behind the UKF is it is easier to approximate a Gaussian distribution than it is to approximate an arbitrary nonlinear function. Instead of linearizing using Jacobian matrices as in the EKF and achieving first-order accuracy, the UKF uses a deterministic sampling approach to capture the mean and covariance estimates with a minimal set of sample points. The UKF was first proposed by Julier, et al. (1995) to address nonlinear state estimation in the context of control theory. The state distribution is also approximated by a GRV, but is represented using a minimal set of sample points. These sample points are carefully chosen so as to completely capture the true mean and covariance of the GRV. When the sample points are propagated through the true nonlinear system, the posterior mean and covariance can be captured accurately to the 2nd order of Taylor series expansion for any nonlinear system. The first step in the UKF is to sample the prior state distribution, i.e., generate the sigma points through the unscented transformation (UT) (Julier, et al. 2000; Julier, 2002; Julier and Uhlmann 2002),which is a method for calculating the statistics of a random variable which undergoes a nonlinear transformation. The basic premise is that to approximate a probability distribution is easier than to approximate an arbitrary nonlinear transformation. The mapping of the UKF versus that of the EKF, through the transformation of nonlinear function f(.) and its Jacobian/Hessian, can be illustrated by Figure 1 (Li et al. 2006). The dot-line ellipse represents the true covariance; the solid-line ellipse represents the calculated covariance. The UKF approach estimates are expected to be closer to the true values than the EKF approach. Consider an n dimensional random variable x, having the mean
The implementation algorithm of UKF is summarized as follows:
The Strong Tracking AlgorithmZhou and Frank (1996) proposed the concept of strong tracking Kalman filter. In the algorithm, the time-varying suboptimal scaling factor is incorporated, for on-line tuning the covariance of the predicted state. As a type of AKF, the STF is essentially a nonlinear smoother algorithm that employs suboptimal multiple fading factors (Xia,1994), in which the softening factors are involved. Based on the idea as in the AKF, the synthesis of UKF and strong tracking filter leads to the strong tracking unscented Kalman filter (STUKF). As in the STKF, suboptimal fading factors are introduced into the nonlinear smoother algorithm:
The fuzzy Logic Adaptive System (FLAS)A FLAS mechanism can be incorporated for determining the softening factor, leading to the fuzzy strong tracking unscented Kalman filter (FSTUKF). The FSTUKF is composed of the FLAS, the strong tracking mechanism, and the UKF. The characteristics of the fuzzy adaptive system depend on the fuzzy rules and the effectiveness of the rules directly influences its performance. The defuzzification is used to provide the deterministic values of a membership function for the output. Using fuzzy logic to infer the consequent of a set of fuzzy production rules invariably leads to fuzzy output subsets. Fuzzy modeling is the method of describing the characteristics of a system using fuzzy inference rules. The parameters for checking the degree of divergence (DOD) to identify the degree of change in vehicle dynamics need to be defined. The innovation information at the present epoch is employed for timely reflecting the change in vehicle dynamics.
An Experiment on GPS/INS Navigation State EstimationThe differential equations describing the two-dimensional inertial navigation state, where two accelerometers and one gyroscope are involved, are (Farrell and Barth 1999):
where[ au , av] are the measured accelerations in the body frame, ωr is the measured yaw rate in the body frame. The error model for INS is constructed by the navigation states augmented by the accelerometer biases and gyroscope drift:
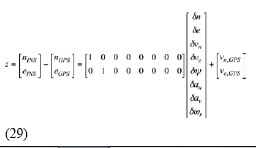
which were utilized in the integration Kalman filter as the inertial error model. In (28), δn and δe represent the east, and north position errors; δvn and δve represent the east, and north velocity errors; δψ represents yaw angle; δau, δav , and δωr represent the accelerometer biases and gyroscope drift, respectively. The measurement model is written as
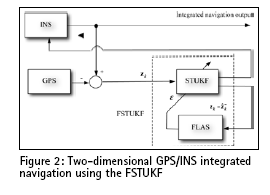
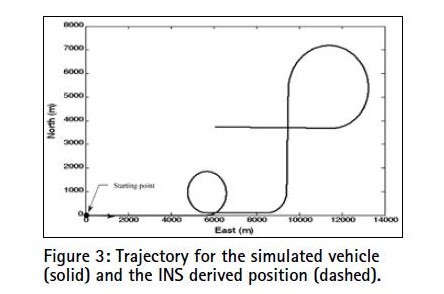
Assume that the differential GPS mode is used, and only the multipath and receiver thermal noise are included. Figure 2 shows the architecture of the loosely-coupled GPS/INS integrated navigation based on the FLAS-coupled STUKF mechanism. The dynamic characteristics of the vehicle can be approximately divided into two categories: (a) constant-velocity straightline motion during four time intervals, 1~180, 361~450, 496~630 and 901~1080s, all at a speed of m/s; (b) circular motion during 181~360, 451~495 and 631~900s. The trajectory for the simulated vehicle is shown as in Figure 3. The parameters utilized in the STUKF are as follows: α=1e-4, β=2, k=0, η=0.25, ρ=0.1. The numerical efficient and stable method such as the Cholesky factorization has been used in obtaining the sigma points. In the FSTUKF, the softening factor ε is determined by the FLAS. The philosophy for defining the rules is straightforward:
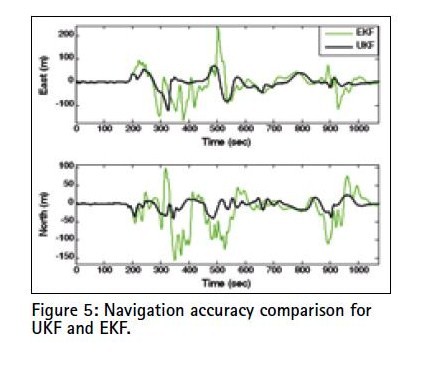
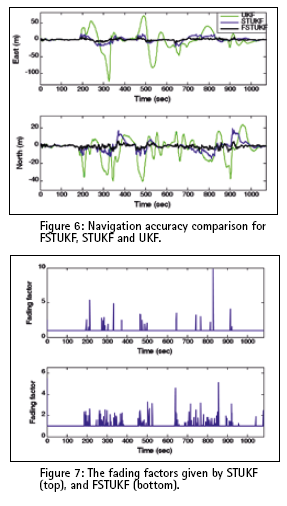
Performance comparison between UKF and EKF is shown in Figure 5;Navigation accuracy comparison for FSTUKF, STUKF and UKF is illustrated in Figure 6. A single fixed value of ε, whether larger or smaller, is not easy to fit the accuracy requirement in all types of environments and is therefore unrealistically in practical applications. Figure 7 shows the fading factors resulting from STUKF and FSTUKF, respectively. For the three regions of high dynamic environments, the fading factors using FSTUKF have been amplified at a higher rate as compared to the STUKF.
Two remarks are given concerning the experiment. (1) In the four time intervals, 1~180, 361~450, 496~630 and 901~1080s, the vehicle is not maneuvering and is conducting constant-velocity straightline motion. For this case, all the filters provide equivalently good results. The navigation accuracies based on the four approaches have relatively small difference. By use of the T-S fuzzy logic, the FLAS senses smaller values of DOD parameters, and gives a larger softening factor. With large softening factors, the UKF, STUKF, and FSTUKF deteriorate to the EKF, and the navigation accuracies based on all the filters are equivalent. (2) In the three time intervals, 181~360, 451~495 and 631~900s, the vehicle is maneuvering. The mismatch of the model leads the STUKF to larger navigation error while the FLAS timely detects the change of DOD parameter, and then reduces softening factor so as to maintain good tracking capability. ConclusionsAn alternative state estimation technique called the fuzzy strong tracking unscented Kalman filter has good potential as the GPS/INS navigation state estimation technique. The approach is designed so as to improve the navigation accuracy at the high dynamic regions while preserving/without sacrificing the precision at the lower dynamic regions. Traditional strong tracking Kalman filter for determining the softening factors heavily relies on personal experience or computer simulation using a heuristic searching scheme. In this article, the fuzzy system has been employed to improve the STUKF performance. Through the use of fuzzy logic, the FLAS has been incorporated into the STUKF as a mechanism for timely detecting the dynamical changes and implementing the on-line tuning of the softening factors by monitoring the innovation information so as to maintain good estimation accuracy and tracking capability. Performance comparisons on EKF, UKF, STUKF and STUKF have been conducted. As the improved version of STUKF, the FSTUKF algorithm leads to very promising results in both navigational accuracy and tracking capability and has very god potential as an alternative navigation state estimator. AcknowledgementsThis work has been supported in part by the National Science Council of the Republic of China under grant NSC 96-2221-E-019-007 and NSC 97-2221-E-019-012. ReferencesBrown, R. and Hwang, P. (1997). Introduction to Random Signals and Applied Kalman Filtering. John Wiley & Sons, New York. Ding, W., Wang, J. and Rizos, C. (2007). Improving Adaptive Kalman Estimation in GPS/INS Integration. The Journal of Navigation, 60, pp. 517-529. Farrell, J. and Barth, M. (1999). The Global Positioning System and Inertial Navigation, McCraw-Hill professional. Gelb, A. (1974). Applied Optimal Estimation. M. I. T. Press, MA. Hide, C., Moore, T., and Smith, M. (2003). Adaptive Kalman filtering for low cost INS/GPS, The Journal of Navigation, 56, pp. 143-152. Julier, S. J. (2002). The scaled unscented transformation, in: Proceedings of the American Control Conference, Anchorage, USA, pp. 4555-4559. Julier, S. J., Uhlmann J. K. and Durrant-whyte H. F. (1995). A new approach for filtering nonlinear system, in: Proceeding of the American Control Conference, pp. 1628-1632. Julier, S. J., Uhlmann J. K. and Durrant-whyte HF (2000). A new method for the nonlinear transformation of means and covariances in filters and estimators, IEEE Transactions on Automatic Control, 5(3), pp. 477-482. Julier, S. J. and Uhlmann, J. K. (2002). Reduced sigma point filters for the propagation of means and covariances through nonlinear transformations, in: Proceeding of the American Control Conference, pp. 887-892. Jwo, D.-J. and Lai, C.-N. (2008), Unscented Kalman filter with nonlinear dynamic process modeling for GPS navigation, GPS Solutions, 12 (4), pp. 249-260. Jwo, D.-J. and Lai, S.-Y. (2008), Fuzzy strong tracking unscented Kalman filter design for integrated navigation, in: Proceedings of the international Symposium on GPS/GNSS 2008, Tokyo, pp.353-362. Jwo, D.-J. and Lai, S.-Y. (2009), Navigation integration using the fuzzy strong tracking unscented Kalman filter, The Journal of Navigation, 62(2), pp.303-322. Li, Y., Wang, J., Rizos, C., Mumford, P. J., Ding, W. (2006). Low-cost tightly coupled GPS/INS integration based on a nonlinear Kalman filter design, in: Proceedings of the U.S. Institute of Navigation National Tech. Meeting, 958-966. Mehra, R. K. (1972). Approaches to adaptive filtering, IEEE Trans. Automat. Contr., AC-17, pp. 693-698. Mohamed, A.H. and Schwarz, K. P. (1999). Adaptive Kalman filtering for INS/GPS, Journal of Geodesy, 73, pp. 193-203. Sasiadek, J. Z., Wang, Q. and Zeremba, M. B.(2000). Fuzzy Adaptive Kalman filtering for INS/GPS data fusion, in: Proc. 15th IEEE int. Symp. on intelligent control, Rio, Patras, Greece, pp. 181-186. Simon, D., (2006). Optimal State Estimation, Kalman, H∞, and nonlinear approaches, John Wiley & Sons, New York. Takagi, T. and Sugeno, M. (1985). Fuzzy identification of systems and its application to modelling and control, IEEE Trans. Syst., Man, Cybern., vol. SMC-15, no.1, pp. 116-132. Wan, E. A. and van der Merwe, R. (2000). The unscented Kalman filter for nonlinear estimation, in: Proceedings of Adaptive Systems for Signal Processing, Communication and Control (ASSPCC) Symposium, Alberta, Canada, pp. 153-156. Wan, E. A. and van der Merwe R. (2001). The Unscented Kalman Filter, in: Simon Haykin (Ed.), Kalman Filtering and Neural Networks, Wiley, (Chapter 7). Xia, Q., Rao, M., Ying, Y. and Shen, X. (1994). Adaptive fading Kalman filter with an application, Automatica, 30, pp. 1333-1338. Zhou, D. H. and Frank, P. M. (1996). Strong tracking Kalman filtering of nonlinear time-varying stochastic systems with coloured noise: application to parameter estimation and empirical |
||||||||||||||||||||
|
||||||||||||||||||||
|
||||||||||||||||||||
|

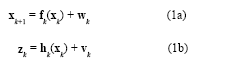
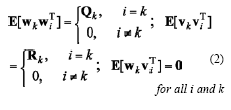







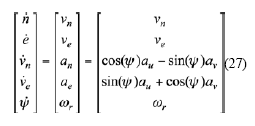

















 (1 votes, average: 1.00 out of 5)
(1 votes, average: 1.00 out of 5)





Leave your response!