| Navigation | |
Analysis of integrated navigation with GPS source variability
 |
|
||||
 |
|
||||
 |
|
||||
 |
|
||||
Guidance and steering control systems that are now in widespread use by farmers for ploughing and cultivating the land with unprecedented accuracy, require centimetre-level position as well as attitude information accurate to a few degrees. Additionally, position and attitude update rate of no less than 10Hz is required for successful guidance in agricultural environments. Guidance and steering control systems rely particularly on heading and roll measurements to steer the tractor on parallel straight lines or curves known as plough lines.
At UNSW, an Attitude and Heading Reference System known as AhrsKF has been developed for a new generation of guidance and steering control system (operated commercially by Leica Geosystems as “mojoRTK”). A Kalman filter (KF) is the most common estimation engine for integrated navigation systems. The AhrsKF system is based on a closed loop KF. It uses strapdown Inertial Navigation System (INS) computation equations in the navigation coordinate system (n-frame). The hardware system makes use of automotive-grade MEMS inertial sensors. In AhrsKF, the GNSS solutions of position and velocity are fed into the Kalman Filter for state error estimation of the INS measurements [1]. A dual frequency survey grade GPS/GLONASS receiver provides position information. An alternative position information source to RTK (Real Time Kinematic) is used in AhrsKF. This is a positioning algorithm that benefits from a relative Pseudorange/Delta-Phase (PDP) filter (commercially know as GL1DE) leading to an enhanced solution of 1 meter accuracy over 20 minutes [2]. The PDP filter provides a filtered position and velocity solution based on assumed vehicle dynamics, and relies heavily on Doppler measurements.
The PDP is not regarded as the main position input for the mojoRTK system. The reason the PDP algorithm is used in the mojoRTK system is to provide stable position inputs when the line of sight to the RTK based station is obstructed. In this paper it is shown that the attitude solutions from AhrsKF are more accurate when PDP, which provides much less accurate positions than RTK, is used. For integrating the PDP solution into the AhrsKF, first both PDP and RTK solutions are sequentially fed into the AhrsKF. Then the integration uses a Multiple Model Kalman Filter (MMKF) that enables the AhrsKF to accommodate both GPS input sources. The sequential and MMKF algorithms attitude solutions are tested with reference to multi-antenna GPS or long boom attitude solutions.
AhrsKF hardware system
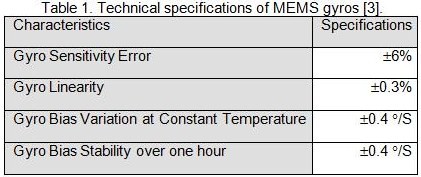
The guidance and steering control system sensors consist of three rate gyros, a three axis accelerometer, and a 2-axis magnetometer. In addition to these sensors, the system includes two GPS receivers – a dual frequency L1/L2 GPS/GLONASS receiver and a low-cost L1-only single frequency GPS receiver which produces a two axis attitude solution used for estimating the biases of the inertial sensors. The inertial and GPS data are then processed by an embedded 400MHz PowerPC processor. The specifications of the MEMS gyros in the guidance and steering control system are listed in Table 1.
In this guidance and steering control system the temperature-compensated inertial data are fed into the integration Kalman filter. In AhrsKF software the GPS position and velocity are used to derive the position and velocity errors of the INS in a closed loop. This means that the error corrected INS position and velocity solutions are integrated with the next epoch GPS solution. The AhrsKF state vector is [1]:
The first three states are attitude errors, then velocity errors, and position errors. The final 6 states are sensor error terms (respectively related to three gyros and three accelerometers), which are modeled as a random walk in the AhrsKF. The measurement equations for velocity and position are [1]:
When the speed of the vehicle is high enough, e.g. 3m/s, the GPS velocity can be used to derive the heading at an accuracy of about 0.57deg (assuming a GPS velocity error of 3cm/s). The heading derived from the GPS velocity can then be used to correct the INS heading in the integration Kalman filter [1]:

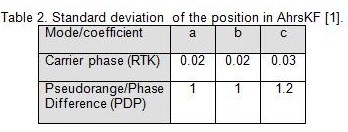
where a, b, and c are the standard deviation of the 3D GPS positions, with the adopted values listed in Table 2.
Test and Setup
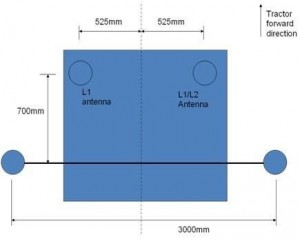
A test was conducted at Boonah, at Leica’s test farm near Brisbane, Australia, on 12 July 2010. In the test, multiple GPS receivers (used to derive the attitude solution as the reference to evaluate the AhrsKF solution) and the mojoRTK were mounted on the tractor. The installation of the GPS antennas is illustrated in Figure 1. The longest baseline is 3m, from which the heading and roll can be derived with an accuracy of 0.056deg (3mm/3m=0.056deg by assuming 3mm accuracy of the double-differenced carrier phase measurements). The forward component of the baselines is 700mm, and the derived pitch has an accuracy of 0.25deg (=3mm/700mm), thus the boom GPS-derived attitude is accurate enough to evaluate the AhrsKF solution. Details of the GPS attitude algorithm used for this test can be found in [4]. There was no obstruction to the RTK base station line of sight during the test.
Figure 1. Leica’s autonomous farming tractor (left), and installation scheme for the GPS antennas (right)
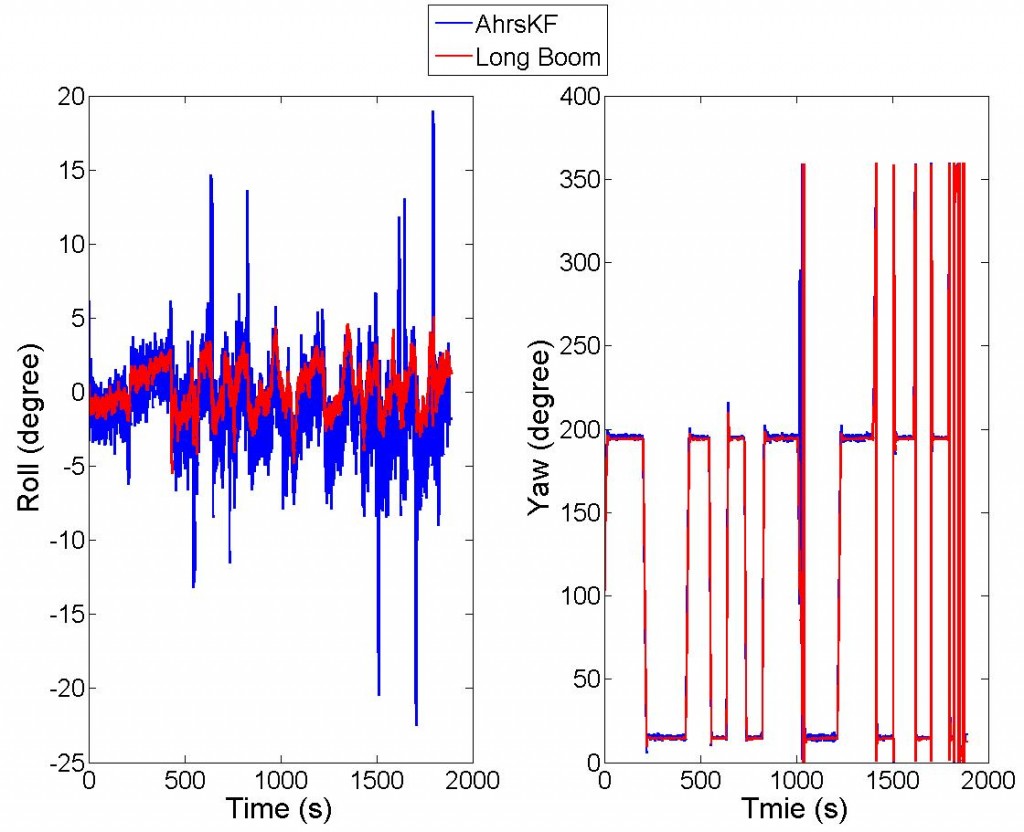
The tractor was driven at a speed of 2-5m/s along straight lines, and about 2m/s at turns. The field is relatively flat, with both the roll and pitch angles being within ±2deg (1 ). The AkrsKf and multi-antenna GPS attitude solutions are depicted in Figure 3, where the AhrsKF solution is plotted as the blue line and the boom GPS solution in red. It can be seen that the AhrsKF solution coincides with the GPS solution and correctly tracks the changes of all attitude angles. It can also be seen that the AhrsKF solution is noisier than the GPS solution. The AhrsKF solution is obtained by post processing the collected data during the test. Only yaw and roll outputs are plotted here since the auto steering system only uses the yaw and roll measurements.
Figure 2. The trajectory of the tractor during the test
Figure 3.
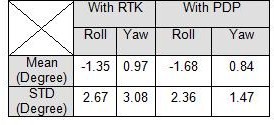
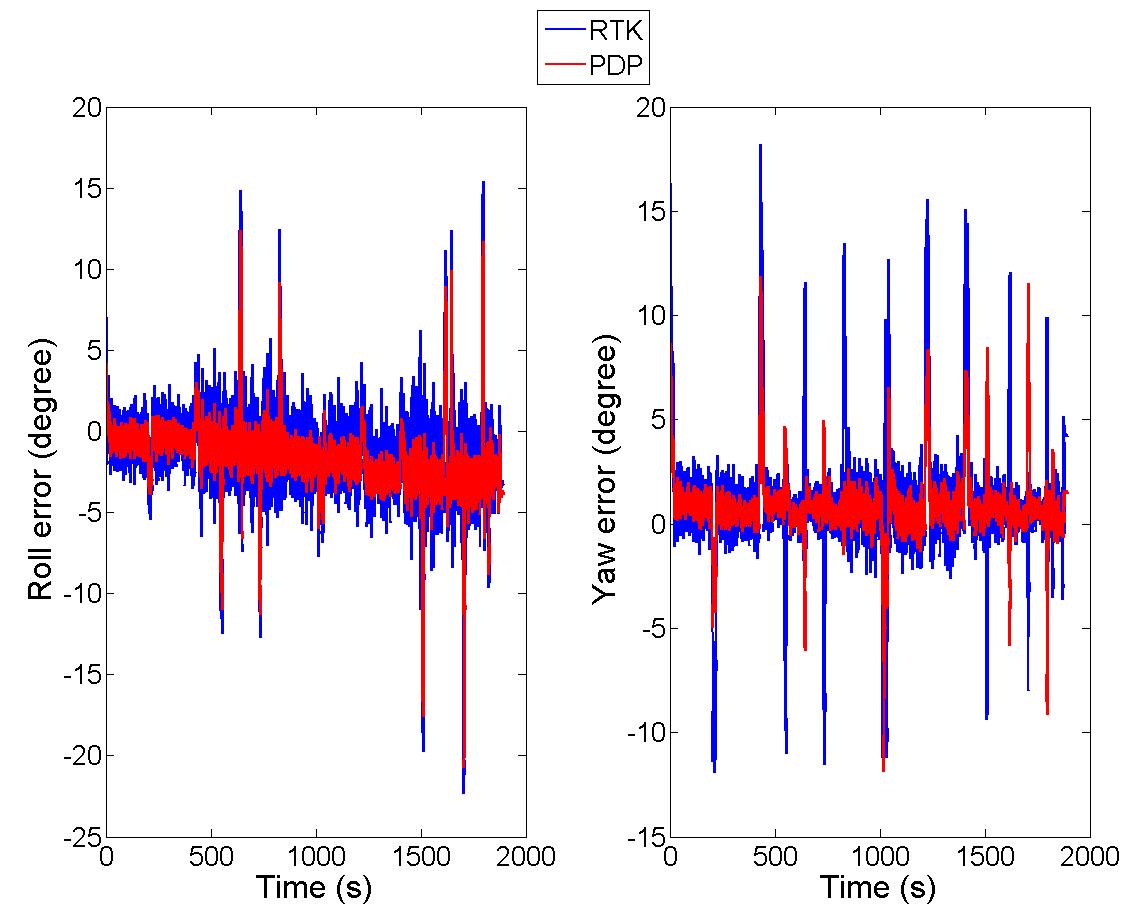
Figure 4 and Table 3 show that AhrsKF can produce less jittery (noisy) and smoother attitude solutions when it is supplied with PDP position, velocity and heading solutions relative to when it is operating with RTK solutions. The table shows the static results of the attitude error relative to the long boom attitude solution. Generally speaking the STD of attitude error for both roll and yaw are lower for the PDP-driven solution. The sudden hikes in the errors are related to time lags when the tractor has sharp turns.
Table 3. Static results for the comparison between post processed AhrsKF solutions with different information sources and long boom attitude solutions
Figure 4. The comparison between roll (left) and yaw (right) errors for post processed AhrsKF solution with RTK and PDP positions relative to multi-antenna attitude solution.
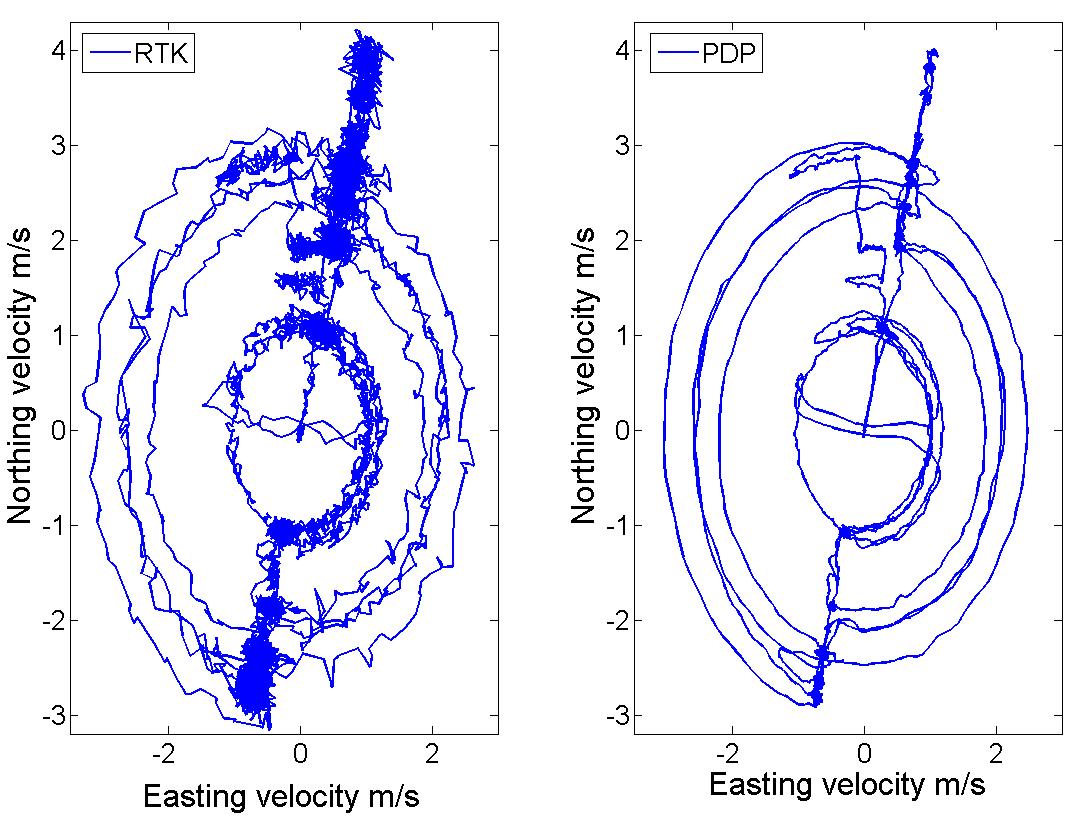
The reason for the better performance of AhrsKF with PDP relative to RTK rests in the mechanism by which PDP solutions are derived and also in the excellent quality of velocity measurements. The PDP solution optimizes the absolute positioning accuracy of the GPS code observation and leverages the relative stability of the GPS carrier phase and Doppler observations [2]. Thus, the PDP filter produces a very smooth solution with consistent rather than absolute position accuracy. There is typically less than 1 cm difference from epoch to epoch [2]. Figure 5 shows the velocity trajectory of RTK and PDP solutions. It is clear that the velocity trajectory of PDP is smoother and has less jitter or noise. The high quality of velocity measurement reflects excellently on the performance of AhrsKF. This is because the northing and easting velocities are used to derive the heading (or yaw) as a measurement input (see Equation 3) to the AhrsKF at each epoch.
Figure 5. The velocity trajectory for RTK solution (left) and PDP solution (right). The PDP {this is the first tiem you’ve mentioned Glide – use either that, or PDP or if you use both use them both earlier} trajectory is visibly smoother.
Multiple model Kalman filter
A Multiple Model Kalman Filter (MMKF) is a way to combine several parallel KF solutions together and to from a filter bank. This is also known as a federated KF. Each KF denoted by an index i, is based on independent information from other filters, e.g. different measurement sources, different R or Q matrices or even different initial P matrices.
The MMKF is the default candidate for making use of both the PDP and RTK solutions in AhrsKF simultaneously and in parallel to each other. The MMKF enables integrating the solutions of two KFs, one operated by RTK and the other operated by PDP in a single estimator. The simplest ways to perform this are one of the following [5]:
1. Weighted fix: weighted averaging of the solutions and their process covariance noises.
2. Best fix: accepts the solution with the highest probability and rejects others.
In either case the weights are calculated by [5]:
where m is the number of components of the measurement vector, l is the number of filter models and the measurement innovation is generally defined as:
The best fix filter simply chooses the solution (hypothesis) with the highest weight. The weighted fix process can be based on predetermined fixed weights. In the weighted fix MMKF with adaptive weights, the filter model or hypothesis with the smallest normalized measurement innovation is allocated the largest probability, and is regarded as most consistent with the measurement stream. Over time the probability of the best hypothesis will approach unity, while others approach zero. If that’s the case the filter cannot go back to the adaptive mode. To avoid this, the weights must be reset to an initial value after a fixed interval of epochs if the zeroing happens. The overall state estimate and error covariance are obtained as follows [5]:
Simultaneous RTK and PDP
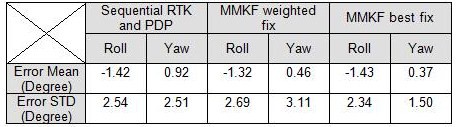
For the purpose of making simultaneous use of RTK and PDP solutions in AhrsKF, three algorithms were used. First, integrating the PDP solution into the AhrsKF, the PDP and RTK solutions can be fed into AhrsKF sequentially. This means that if at epoch k, the AhrsKF is fed by PDP solution then the next epoch it is fed by the RTK solution. Note that both frequencies of the RTK/GPS and the PDP were set at 10 Hz. The other two approaches to RTK/PDP simultaneous utilization in AhrsKF include weighted-fix MMKF and best-fix MMKF. All three algorithms results were obtained by post processing using PDP and RTK data from the same test already described. The long boom GPS solution was again used as the reference and the static results are shown in table 4, as well as Figure 6a and 6b.
The quality of the sequential algorithm solution is exactly between that of AhrsKF with RTK and AhrsKF with PDP, in terms of both the error mean and the error STD. On the contrary, the MHKF with weighted fix technique leads to no better performance than AhrsKF with RTK or with PDP. However, the best performances for both roll and yaw and in terms of both error mean and error STD are achieved by the best fix MHKF. This may be due to the fact that the PDP positions are not stable over longer periods than 20 m, suggesting that RTK helps in stabilizing the overall solution.
Table 4. Static results for the comparison between different algorithms based on the post processed AhrsKF solutions simultaneously fed with both GPS/RTK and PDP with long boom GPS attitude solution.
Figure 6. The roll and yaw errors for sequential algorithm (a and b), weighted fix MHKF (c and d) and best fix MHKF (e and f).
Conclusion
GNSS/INS (Global Navigation Satellite System/Inertial Navigation System) systems have found widespread use in industry, especially in automated agriculture. Automated agriculture requires high frequency, precise, steady and smooth attitude solutions. These together with stringent cost requirements, necessitate smart integration algorithms. Given that navigation solutions can be derived from different information sources, combining several information sources can result in smoother attitude solutions relative to when a single information source is utilized. A Multiple Model Kalman Filter (MMKF) is used for this purpose. The results show that the fine attributes of both information sources, namely RTK and PDP, are adequately captured by best fix MHKF.
References
[1] Y. Li, et al., “Attitude determination by integration of MEMS inertial sensors and GPS for autonomous agriculture applications,” GPS Solutions, pp. 1-12, 2011.
[2] NovAtel. (2008, Application Note on Pseudorange/Delta-Phase (PDP) and GL1DE Filters. Available: http://www.Novatel.com
[3] Y. Geng, et al., “Developing a Low-Cost MEMS IMU/DGPS Integrated System for Robust Machine Automation,” in Fort Worth, Texas, 2007, pp. 1618-1624.
[4] Y. Li, et al., “Calibrated MEMS Inertial Sensors with GPS for a Precise Attitude Heading Reference System on Autonomous Farming Tractors,” in ION-GNSS, GA, Savannah, 2009.
[5] P. D. Groves, Principles of GNSS, Inertial, and Multisensor Integrated Navigation Systems. London: Artech House, 2008.
To read the article in Polish language visit: http://webhostinggeeks.com/science/source-variability-pl
My Coordinates |
EDITORIAL |
|
His Coordinates |
Dr Shailesh Nayak |
|
Mark your calendar |
July 2011 TO December 2011 |
|
News |
INDUSTRY | LBS | GPS | GIS | REMOTE SENSING | GALILEO UPDATE |

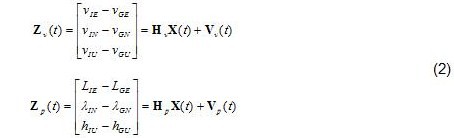


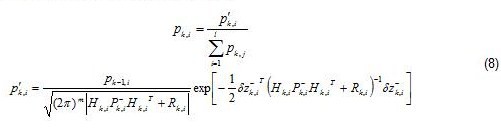
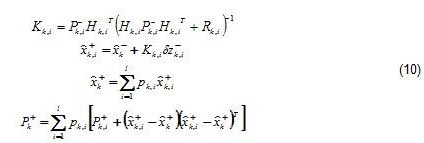












 (2 votes, average: 1.00 out of 5)
(2 votes, average: 1.00 out of 5)





At UNSW, an Attitude and Heading Reference System known as AhrsKF has been developed for a new generation of guidance and steering control system