Collision avoidance by speed change

James L Farrell Vigil, Inc.,, Severna Park, Maryland, USA

Collision avoidance is one operation for which the many advantages of satellite navigation have not been developed. As noted in [1] the magnitude, multiplicity, – and importance – of potential benefits combine to make a compelling case for further consideration:

Integration : one system for both 3-D (in-air) and 2-D (runway incursions)

Autonomy : no ground station corrections required

Communication : interrogation / response replaced by ModeS squitter operation

Coordination : garble elimination through coordinated squitter scheduling Tracking : all tracks maintained with GPS pseudoranges in data packets

Dynamics : tracks provide optimally estimated velocity as well as position

Timeliness : latency is counteracted through history of dynamics with position

Multitarget handling : every participant can track every other participant

Control : collision avoided by acceleration / deceleration rather than climb/dive

Recognition of these advantages over the existing pre-GPS Traffic Alert and Collision Avoidance System (TCAS) has led NASA to support efforts toward exploiting these improvements. Details of the arrangement between NASA and Ohio University are described in [2] and [3] ; work described herein is part of that overall investigation. Previous work is summarized only briefly here; present emphasis is on results.

As part of the NASA-sponsored effort, specific numerical results were generated for preventing conflicts impending with two aircraft (an “intruder” and an “evader”) initially on a collision course. Over a wide range of conditions (i.e., intruder and evader speeds; angles between their velocity vectors), amounts of speed change required to produce a specified miss distance are readily computed. Results for sample conditions are plotted, along with the time to closest approach (which, due to the speed change, deviates from the time-to collision). The plots are followed by recommendations for adaptation to existing and future operation.

Existing methodology

An abbreviated description is given here for TCAS [4] which uses the history of range (instantaneous value of separation distance) and its rate of change to decide whether an advisory is needed. When the range is decreasing, the ratio of range to that closing rate, called time to go (TTG), is given the notation

= (range) / (closing rate) (1)

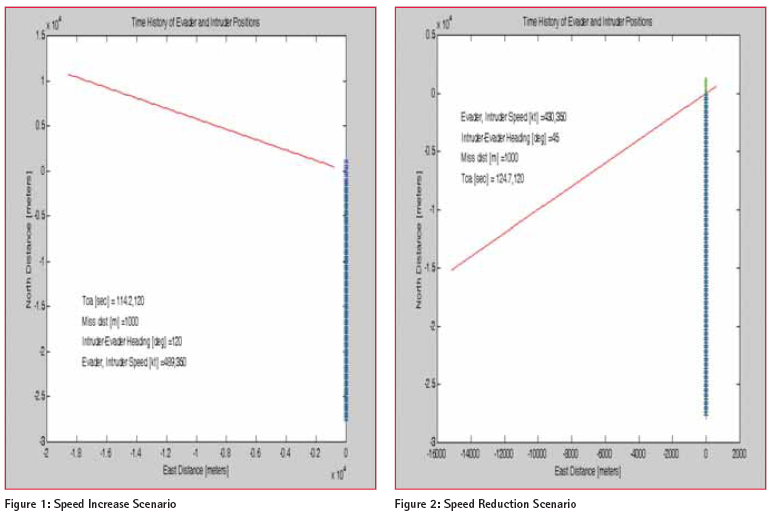
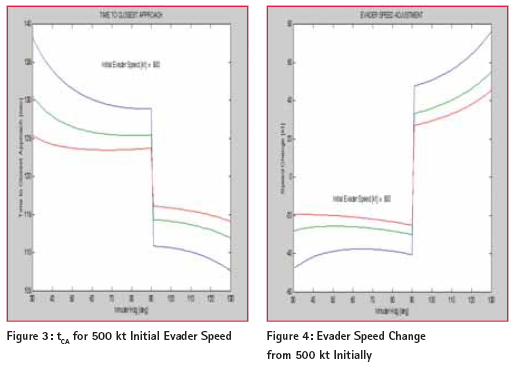
That value is the time to collision for two aircraft on a collision course, characterized by zero rotation rate for the line-of-sight (LOS). Nonzero LOS rates produce, instead of a point of collision, a point of closest approach (PCA) and the corresponding closest approach time deviates from ; TCAS applies “DMOD” adjustments in an effort to account for those departures.

Considerations just described are used to determine whether alerts or actions are needed. When evasive maneuvers are deemed necessary, they take place in a vertical plane; one aircraft climbs as the other dives.

TCAS limitations

A casual Internet search can uncover much concern about the abruptness – and a potential for unnecessary “dodgesjust- in-case-the-azimuth direction…” – and the safety – of the climb / dive combination. Those and other capability restrictions are traceable to limited pre- GPS technology – highly dependent on transponders. With available information consisting of highly accurate range and less accurate altitude, imprecise nature of the latter is not the main limitation; note the absence of timely horizontal crossrange (azimuth) measurements. Although cross-range estimates can be deduced from histories of range and ownship dynamics, those estimates evolve only indirectly, critically dependent upon LOS rotation; they are neither as accurate nor as timely as needed. Indeed, LOS rotation sufficient to provide azimuth observability occurs only at close ranges – precisely the condition necessary to avoid.

Absence of direct azimuth measurement data translates immediately to absence of most beneficial features listed in the Introduction. Rather than a criticism of TCAS design, then, a comparison of capability is presented here as an intrinsic result of a fundamental trait: direct 3-D observability. In addition, the proposed methodology will offer feasibility of operating with an intruding aircraft being

• oblivious to imminent danger, thus nonmaneuvering

• nonparticipating altogether; by operational extensions not shown here but covered on p. 203 of [5].

Modernized approach

With extended squitter data containing direct GPS measurements [2,3,6], all major error sources either cancel or can be readily rejected by straightforward data editing [7]. A host of advantages materialize instantly [8]. Track files are obtained and maintained from that comparison of time- stamped raw GNSS measurements. Errors in perceived position – including errors in projected future distances near PCA – can then be made smaller than requisite miss distances. The projected future miss distances can be enlarged through speed control decisions based on the accurate 3-D track files.

Speed can be increased or decreased, whichever is deemed most suitable. Once a speed change is prescribed there is no reason to delay action; they are treated here as instantaneous but not excessive since

• abrupt speed increase is impractical if unduly large

• large reductions in speed risk stall.

Applicable conditions

Before addressing the most general class of conditions, a meaningful set of guidelines governing two aircraft must be clearly established. Scenarios to be considered here thus consist of two moving participants, termed intruder and evader.There can be, in addition, stationary observers (e.g., a tower) monitoring – and possibly communicating with – either or both of them. For maximum safety the selected methodology will enable success when the intruder is oblivious to any danger; thus corrective action is assigned only to the evader.

Not every dangerous scenario is amenable to solution via speed change. Deceleration, for example, cannot avert a head-on collision. By extension of that reasoning, faster closing rates tend to demand wider variations in speed. Using that rationale, then, a first step is to impose some limits on applicable geometries. Criteria involving range and closing rate, already described, will likewise be used here.

Depending on the evader and intruder velocity directions, the closing rate may be greater or less than evader speed. With higher closing rates being the most challenging (again by extension of the limiting head-on case), it is not surprising that they offer the narrower span. To preclude excessive demands for speed change, values exceeding 130⁰ or less than 30⁰ are considered candidates for resolution by turns, beyond scope here. Within the 30⁰ – 130⁰ spread it was found expedient to increase speed for heading differences above 90⁰ and reduce it below.

Illustrative examples

For the scenario in Figure 1 the origin is set at the point where collision would occur in two minutes if no corrective action ever happened. With a 450-knot (231.65 m/ sec) initial speed the evader then begins at a location 231.65 × 120 = 27798 meters from the origin. Depicting that location here along the North/South line does not affect the computed results – a simple subtraction (intruder heading) – (evader heading) will rotate the cardinal directions relative to the image in a more general case. The 350- knot intruder starts from a location backed away from the origin, along a 120⁰ line (heading is synonymous with ground track in this simplified analysis), by 180.17 × 120 = 21620 meters. By orienting one reference direction (here the y-axis) of the ENU coordinate frame along the evader’s path, only that y-component of speed change v need be computed. Given the separation vector R at any time (e.g., for the initialization just shown), the requisite speed change is formedbtracting [0 v]^T from the initial (intruder – evader) relative velocity, forming the unit vector n perpendicular to that direction, and setting the component of R along n equal to a chosen a scalar miss distance D (1 km). Imposing that condition produces a quadratic equation, offering an increase and a decrease in speed, both of which conform precisely to D. In either case the time t_CA to closest approach (computed by nulling the component of R parallel to the post-acceleration / deceleration relative velocity vector) deviates from the two-minute time-to-collision.

For the next example a case was run with similar parameters (2 min, 1 km, 450 kt, 350 kt) but with a 45⁰heading difference. Once again the minimal separation distance (1 km) occurs when R becomes perpendicular to the relative velocity, computed by simple time extrapolation as described at the end of the preceding paragraph. In this case that happens at a later time since (recall the end of the preceding section), speed reduction was chosen; thus t_CA exceeds the twominute time-to collision in this case.

While the first scenario evolves in a way easily visualized from Fig. 1 (separation distance decreases until reaching final positions shown), Fig. 2 is slightly more complex. The evader’s actual path (thick line, Northbound) doesn’t reach the intruder’s path until the intruder has passed. An extension of the evader’s path (shown as a lighter, thinner line) shows how it would have progressed without the speed reduction – except that a collision would have occurred where the two paths intersect. A simple animation in the form of a Matlab “movie” appears in [9].

Performance with General conditions

Sets of runs were made for generation of plots showing results obtained with the following parameter values:
• intruder heading at values from 30⁰ to 130⁰

• intruder speed at 200, 300, and 400 knots

• 2 minutes to collision for evader speed at initial value

• initial evader speed at 500 knots

• evader speed change chosen for 1 km miss distance

In all cases the evader was headed due North and, if the evader speed had remained at its initial value, a collision would have occurred at the point designated as the origin. With intruder heading as the abscissa, plots were generated for time to closest approach t_CA< and for evader speed change (increasing for intruder headings above 90⁰ and decreasing below 90⁰, as previously noted). Miss distances obtained were also plotted (to ensure conformance to chosen input values) but, since they were always in precise agreement, there is no need to show those plots here.

The three different intruder speeds are not labeled on the figures but, for these plots, the “inside” curves (those with the smallest speed change and the smallest average t_CA departure from 120-sec) are for the 200-kt intruders; the “outside” curves (those with the largest speed change and the largest average t_CAdeparture from 120-sec) are for the 400-kt intruders; the 300-kt intruders curves lie between.

From running many cases it was found, propitiously but not surprisingly, that lower evader speeds demand smaller amounts of speed change. The same trait holds true for the amount of departure between t_CA and the time-to-collision. It is worth noting that, when the guidance algorithm produces acceptable values for speed change and t_CA, they can be recomputed with miss distance increased to account for uncertainties introduced by tracking errors.

Although not mentioned thus far, and not noted on the plots, all evader flight path modifications indicated here include another feature: a gradual climb, starting at the same time as the speed change. In order to avoid a wake problem (which would otherwise arise from flying through the same air just vacated by the intruder), the evader would be instructed to climb to the same final altitude that TCAS would have prescribed. In marked contrast to TCAS, however, this climb would be gradual. The proposed method, then, provides only half of TCAS’s vertical separation (the intruder can be nonparticipating), but a substantially larger horizontal separation can be commanded.

Recommended future work

It is acknowledged that the results shown here only begin to describe collision avoidance strategies. Refinements can be added (e.g., accounting for wind, finite time elapsed during speed changes, etc.) and, of greater importance, extensions will be needed for three-dimensional scenarios, increased numbers of participants, and turn scenarios for heading differences below 30⁰ or beyond 130⁰. At least in the near term two further modifications are likely to become necessary:

• acceptance of guidance from elsewhere (e.g., tower)

• operation in concert with, rather than substitution for, TCAS.

The last item was described in [3] as a preemptive approach. Rather than providing the whole guidance for collision avoidance, speed changes could be introduced further in advance of PCA, for purposes of preventing TCAS resolution advisories from being generated. Finally, all applicable algorithms and programs will have to be submitted for documentation in a standardized form; this clearly fits within the realm of capabilities too important to be limited by any proprietary claims.

Throughout this development a capability not yet fully realized in operation has been taken for granted. Usage of air-to-air track methods, known from decades-old radar applications [10], must be adapted with GNSS double differences replacing radar observables. Since tracking algorithms in a stable (INS-based) reference frame (summarized in [11] and detailed in Chapter 9 of [5]) have long been established, and since GNSS measurements far surpass radar in accuracy, success of that substitution awaits only a commitment to support a brief extension followed by flight validation.
Means to bring this capability into operation, then, are entirely within reach. The need to follow through is urgent – and the urgency can only grow with increasing occurrence of a recently adopted practice: usage of unmanned aircraft.

Conclusions

Speed change guidance strategy, combined with ModeS extended squitter data containing raw measurements from GPS/GNSS, has long been known to offer enormous advantages in safety, versatility, autonomy, and all aspects of performance for collision avoidance. Quantitative results are easily obtainable for a wide range of applicable scenarios.

Recommendations

It is also recommended that the area of the data be extended as funds become available so that improvement can be made on the models. It will be necessary to carry differential levelling to other parts of Rivers state and indeed, other parts of Nigeria to serve the need of Surveyors and Engineers.

References

[1] Collision Avoidance By Deceleration http://tinyurl.com/JLF-link13

[2] Uijt de Haag, M. and Farrell, James L., “Collision Avoidance for Future Operation,” IEEE-ICNS Conference, Arlington VA, May 2009.

[3] Uijt de Haag, M., Vana, S., and Farrell, James L., “Simulation Model to Evaluate Collision Avoidance Methods using Raw Measurements in the Automatic Dependent Surveillance – Broadcast,” ION-GNSS 2011, Portland OR

[4] Introduction to TCAS II, US DOT-FAA Booklet, March 1990.

[5] Farrell, James L., GNSS Aided Navigation and Tracking, American Literary Press, 2007 – http://tinyurl.com/JLF-link4

[6] Farrell, James L., McConkey, E.D., and Stephens, C.G., “Send Measurements, Not Coordinates,” IONJ v46 n3 1999, pp 203-215.

[7] Single-measurementRAIM http://tinyurl.com/JLF-link17

[8] http://jameslfarrell.com/ gps-gnss/surveillance

[9] http://www.youtube.com/ watch?v=auoNAd-JP4A

[10] Farrell, James L. And Quesinberry, E.C., “Track Mechanization Alternatives,” NAECON Symposium, Dayton Ohio, 1981.

[11] http://jameslfarrell.com/ tracking/cartesianvsspherical The author is indebted to Ohio University for support of this work.