| Positioning | |
Positional accuracy enhancement of an INS/DGPS integrated system
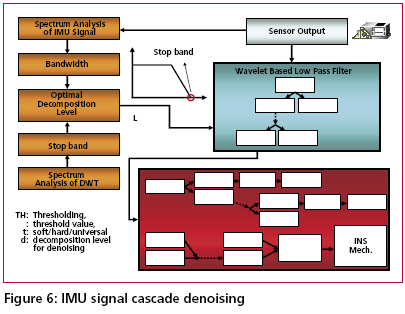
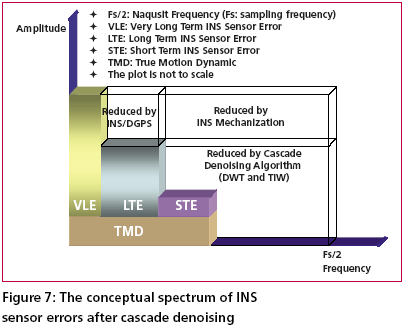
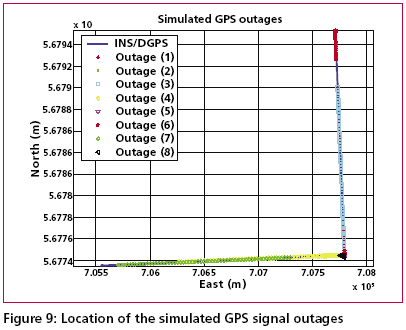
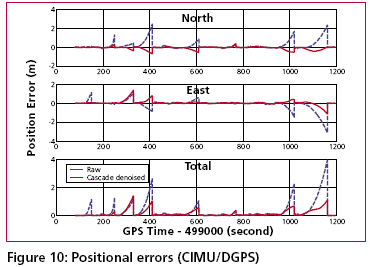
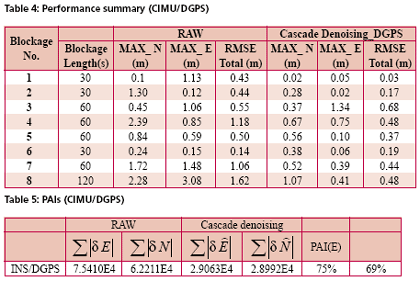
Development of the cascade denoising algorithmAs indicated previously, through a spectrum analysis of the DWT/TIW denoising algorithm and kinematic IMU signals, the bandwidth of the true motion dynamics sensed and the stop band of the wavelet-based low pass filter can be determined as given in Tables 1 and 2. As a result, an optimal decomposition level of the waveletbased low pass filter was determined. Since the signals whose frequency ranges are outside the bandwidth of the true motion dynamics are undesirable, wavelet-based low pass filters with optimal decomposition levels (L) can be applied for each sensor. These low pass filters are first used to remove undesirable high frequency components whose frequencies are higher than the stop bands and then applied to filter any remaining short term errors whose frequencies are lower than the stop bands of the low pass filters, as shown in the Figure (6). Through this spectrum analysis of the cascade denoising algorithm, the above mentioned limitations of the traditional denoising procedure can be removed. In addition, the cascade denoising is able to provide superior performance over traditional denoising algorithms in the position domain. The conceptual plot of the frequency spectrum of the cascade denoising algorithm is given in Figure (7). Comparing Figure (3) to Figure (5) and Figure (7), the spectrum of the cascade denoising resembles that of a perfect denoising algorithm. This implies that the cascade denoising is superior to traditional algorithms in the frequency domain. Furthermore, Chiang et al., [2004] showed that the cascade denoising is superior to traditional denoising algorithms in the position domain since it is capable of providing significant improvements in terms of the positioning accuracy during GPS outages. Results and discussionsTo asses the performance of the proposed cascade denoising algorithm a field test was conducted in October 2003 by the Mobile Multi-sensor Systems (MMSS) research Group of the University of Calgary. The test was conducted to replicate a typical land vehicle environment using three different INS/ DGPS integrated systems consisting of a navigation grade IMU (Honeywell CIMU), and two NovAtel OEM4 receivers. The performance of the cascade denoising algorithm was then evaluated in terms of the IMU qualities (i.e., accuracy levels). Figure (8) illustrates the test van and the set up of the IMU systems used in the test. The reference trajectory was generated using the CIMU/DGPS integrated system with a loosely coupled extended Kalman Filter integration scheme. There were no natural GPS signal outages in this test trajectory, and therefore, eight simulated GPS signal outages were simulated by removing the GPS solutions being fed into the INS Kalman filter during the integration process, see Figure (9) for the location of the simulated outages along the test trajectory. The navigation solutions obtained through the use of raw IMU measurements and denoised IMU measurements were then compared with the reference trajectory. Figure (10) and Table 4 provide summaries of the positional error performances when comparing the denoised INS/DGPS integrated navigation solutions to the raw INS/ DGPS integrated navigation solutions using a navigation grade IMU with the reference trajectory during each GPS signal outage period. It can be seen from Figure (10) that the cascade denoising algorithm was able to provide visible improvements during several GPS outage periods. As indicated in Table 4, the positional errors of six GPS outage periods were successfully reduced using denoised CIMU measurements. The rate of improvement for individual outage periods was 75% (6/8). In addition, the magnitude of improvement ranged from 20 centimeters to 1 meter and the percentage of improvement ranged from 20% to 90%. In contrast, the remaining two GPS outage periods were not significantly degraded by the denoising operation. The magnitude of this degradation ranged from 5 centimeters to 20 centimeters and the percentage of degradation ranged from 20% to 35%. To provide a more accurate description associated with the performance of the cascade denoising algorithm, a performance analysis index can be defined as Where TP is the total number of accumulated points during all GPS outages (t is the total length of all GPS outages and Fs is the sampling rate of the IMU), For navigation grade IMU (i.e., CIMU), the long term errors of the IMU (i.e., bias, drifts) are stable and well behaved. This means that the remaining short term errors of the IMU account for most of the residual position error during GPS signal outages. ConclusionsThis article presented a novel cascade denoising algorithm to reduce the impact of short term INS errors and improve the positioning accuracy during GPS signal blockages using several INS/DGPS integrated navigation systems. The key elements of any pre-filtering operation are to investigate the bandwidth of the true motion dynamics and remove the short term INS errors without deteriorating the true motion dynamic signal. The results of spectrum analyses demonstrated that the bandwidth of the true motion dynamics is very low. In fact, it can be divided into two groups. The first group consists of the XGyro, Y-Gyro, and Z-Accelerometer with corresponding bandwidth ranges from 0 to 6 Hz. In contrast, the second group is composed of XAccelerometer, Y-Accelerometer, and Z-Gyro corresponding to bandwidth ranges from 0 to 1Hz. In addition, the spectrum of the true motion dynamics is independent of the quality of the IMU used. The cascade denoising algorithm developed in this article was able to overcome the limitations of existing denoising algorithms in the frequency domain. In addition, it was capable of providing superior performance in the position domain. The results demonstrated that the cascade denoising algorithm provided the most significant improvement when using a navigation grade (CIMU-=[09) DGPS integrated system; the percentage of improvement reached 58%. For a navigation grade IMU (e.g., CIMU) the long term errors (e.g., bias, drifts) were stable and well behaved, while the remaining short term errors dominated. AcknowledgementsThis study was supported in part by research fund from National Science Council of Taiwan (NSC 95-2221-E- 006 -335 -MY2), the Natural Science and Engineering Research Council of Canada (NSERC) and the Canadian Geomatics for Informed Decisions (GEOIDE) Network Centers of Excellence (NCE). Dr. Eun-Hwan Shin is acknowledged as a co-author of the AINS® toolbox used in the article for providing the INS mechanization and INS/GPS extended Kalman filter. ReferencesBruton, A.M., Skaloud, J., Schwarz, K.P. (1999): The Use of Wavelets for the Analysis and De-noising of Kinematic Geodetic Measurements. Geodesy Beyond 2000- IAG General Assembly, Birmingham, UK, July 19-24, International Association of Geodesy Symposia, Vol. 121, 2000, Springer, 227-232. Chiang, K.W., Hu, H., El-Sheimy, N., and Niu, X. (2004): Improving Positioning Accuracy of a GPS/ MEMS Integrated Vehicular Navigation System During DGPS Outages Periods Utilizing Cascade Denoising Algorithm, GNSS 2004, ION, September 21-24, 2004 – Long Beach, California, USA Chiang, K.W. (2004): INS/GPS Integration using Neural Networks for Land Vehicular Navigation Application, PhD thesis, Department of Geomatics Engineering, The University of Calgary, UCGE Reports 20209 Czompo, T. (1990): Use of Spectral Methods in Strapdown ISS Data processing, Proceedings of the international Symposium on Kinematic System for Geodesy, Navigation and remote sensing, Banff, September 10-14,Springer-Verlag,New York. Coifman, R.R. and Donoho, D.L. (1995): Translation-Invariant De-Noising, Lecture Notes in Statistics, 103,pp.125-150,Yale University and Yale University Daubechies, I. (1992): Ten Lectures on Wavelets. Philadelphia:SIAM. Donoho, D.L. (1992): De-Noising via Soft Thresholding. IEEE Trans. Info. Theory, Vol.41,No.3, May 1995,pp.613-627 Jansen, M. (2001): Noise reduction by wavelet thresholding, New York Springer, Lang M., Guo, H., Odegard, J.E., and Burrus, C. S., and Wells Jr. R. O. (1996): Noise Reduction Using an Undecimated Discrete Wavelet Transform. IEEE Signal Processing Letters, 3(1):10-12, Jan. 1996. Mallat, S. (1989):A Theory of Multiresolution Signal Decomposition: The Wavelet Representation, IEEE Trans.PAMI,11,pp674-693 Mallat, S. (1999): A Wavelet Tour of Signal Processing, Academic Press, 2nd edition, 1999 Nason, G., and Silverman, B.(1995): The stationary wavelet transform and some statistical applications, in Wavelets and Statistics (Antoniadis and Oppenheim eds.), P.281-299 Nasser, S.(2004):Improving the Inertial Navigation System (INS) Error Model for INS and INS/DGPS Applications. PhD thesis UCGE Reports 20183, Department of Geomatics Engineering, The University of Calgary Skaloud, J. (1999):Optimizing Georeferencing of Airborne Survey Systems by INS/DGPS, PhD thesis, Department of Geomatics Engineering, The University of Calgary Strang, G., and Nguyen, T. (1997): Wavelets and Filter Banks. Wellesley-Cambridge Press. |
||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||
|
Pages: 1 2

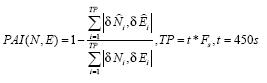














 (No Ratings Yet)
(No Ratings Yet)





