| Geodesy | |
Malaysia precise geoid (MyGEOID)
|
||||
|
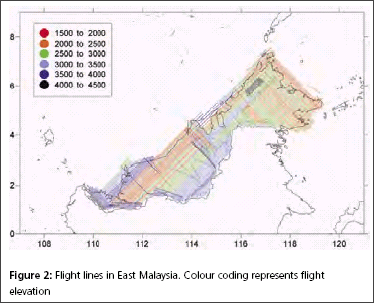
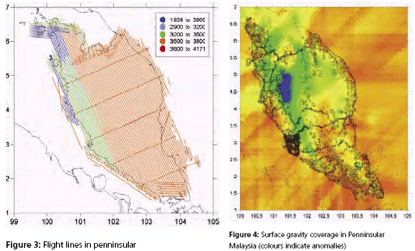
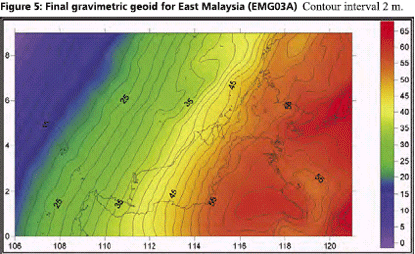
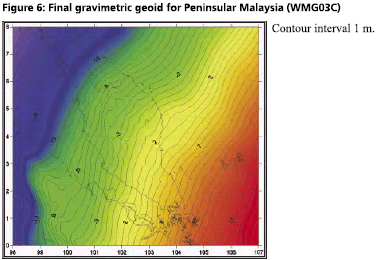
GPS infrastructures that have been established in Malaysia are mainly served as a ground control stations for cadastral and mapping purposes. Another element that has not been utilised is the height component due to its low accuracy. Conventional levelling is still the preferred method by the land surveyors to determine the stations orthometric height (H) with a proven accuracy. Therefore, Department of Survey and Mapping Malaysia (DSMM) has embarked the Airborne Gravity Survey, with one of the objectives is to compute the local precise geoid for Malaysia within centimeter level of accuracy. With the availability of the precise geoid, the “missing” element of GPS system is solved. The Malaysian geoid project (MyGEOID) is unique where the whole country is covered by with dense airborne gravity, with the aim to make the best possible national geoid model. The basic underlying survey and computation work of the Malaysian geoid project was done by Geodynamics Dept. of the Danish National Survey and Cadastre (KMS; since Jan 1 part of the Danish National Space Center) in cooperation with JUPEM. With the new data the geoid models are expected to be much improved over earlier models (Kadir et al. 1998). ObjectivesThe main objective of the Malaysian geoid model (MyGEOID) is to be able to compute orthometric heights H that refer to the national geodetic vertical datum (NGVD). Mathematically, there is a simple relation between the two reference systems (neglecting the defl ection of the vertical and the curvature of the plumb line): where, hGPS is the GPS height above the ellipsoid and N the geoid seperation. In the above equation it is important to realize that H refers to a local vertical datum, hGPS refers to a geocentric system (ITRF/ WGS84), to which the computed (gravimetric) geoid also usually refers. the possibility of using GPS leveling technique, knowing the geoidal height N, the orthometric height H can be calculated from ellipsoidal height h. Deriving orthometric height using this technique with certain level of accuracy, could replace conventional spirit leveling and therefore make the levelling procedures cheaper and faster. The existence of datum bias (differences between geoid and local mean sea level) will not gives satisfactory results if based on the above formula. In order to overcome this problem, fi tting the gravimetric geoid onto the local mean sea level (NGVD) will minimize the effect of datum biases. Gravity data acquisition and processingGravity dataThe Malaysian airborne gravity survey was done on a 5 km line spacing, covering mostly Sabah and Sarawak in 2002 and Peninsular Malaysia in 2003. The airborne gravity data system used was based on the Danish National Space Center (DNSC)/University of Bergen system, used extensively for Arctic gravity field mapping. The system is based on differential GPS for positioning, velocity and vertical accelerations, with gravity sensed by a modifi ed marine Lacoste and Romberg gravimeter. The system has a general accuracy better than 2 mgal at 5 km resolution. For the Malaysia airborne survey, the system was installed in a An- 38 aircraft (Figure 1, below), and the aircraft turned out to be very suitable for the airborne survey, with accuracies estimated from crossovers well below 2 mgal r.m.s. The airborne gravity survey was flown at different elevations, as topographic conditions permitted, see Figure 2 and 3. The data were therefore required to be downward continued to the surface, before applying the Stokes formula gravity to geoid transformation. The downward continuation was done by least-squares collocation using the planar logarithmic covariance model (Forsberg, 1987), using all available gravity data in the process (airborne, surface, marine and satellite altimetry gravity data). The Stokes’ integration was implemented by spherical FFT methods (Forsberg and Sideris, 1993). The existing surface gravity data coverage was only of signifi cance in Peninsular Malaysia (Figure 4). Here the relatively dense surface gravity data coverage in the lowlands will strengthen the geoid compared to the situation in Sabah and Sarawak, where a minimum gravity data was available. Gravimetric GEOID computationFor the Malaysian project new GRACE satellite data combination models were used (GGM01C). This model is a combination model to degree 180 based on 1° mean anomalies, essentially derived from the same terrestrial data as EGM96, but having superior new satellite information (GGM01S) at the lower harmonic degrees. A third data source for the geoid determination is digital terrain models (DEM’s), which provide details of the gravity field variations in mountainous areas (the mass of the mountains can change the geoid by several 10’s of cm locally). The handling of digital terrain models is done by analytical prism integration assuming known rock density (Forsberg, 1984). The new satellite data SRTM was used together with JUPEM DEM’s for this purpose. With the data from spherical harmonic models, local or airborne gravity, and DEM’s, the (gravimetric) geoid is constructed by removerestore techniques as a sum The summary of gravity data used in the gravimetric geoid computation are tabulated in Table 1 and the computed geoid models for Sabah and Sarawak (EMG03C) as in Figure 5 and Peninsular Geoid model (WMG03A) as in Figure 6. |
||||

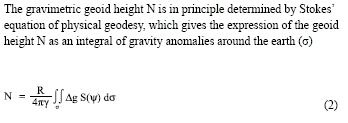













 (No Ratings Yet)
(No Ratings Yet)





