| Positioning | |
INS/TACAN/ALT- an alternative solution for positioning
|
||||||||
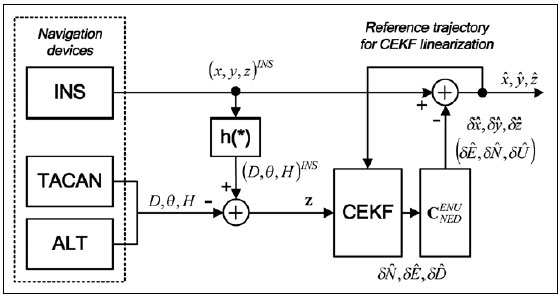
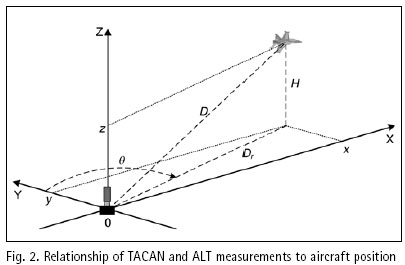
Structure and operation of systemThe system presented in the paper is designed according to the scheme of compensation and processes navigation data with use of a Complementary Extended Kalman Filter (CEKF). The INS/TACAN/ALT system works with a feed-forward correction, i.e. there is no feedback to INS and its errors are corrected externally. The structure of system is shown in the Fig. 1. The INS contains accelerometers and gyros, enabling calculation of linear and angular displacement [2, 9, 10]. Velocity and position of the vehicle are obtained through initialized single and double integration of accelerations, previously transformed from the body frame to the navigation frame of reference [9, 10]. It is assumed here, that INS position (x, y, z)INS will be expressed in an Earth-fixed reference frame OXYZ, with its origin at the location of TACAN ground station and with axes coinciding with the axes of the local horizontal frame of reference ENU (East-North-Up). The assumed frame is suitable for short-range systems, containing a navigation device, which measurements are to be referenced to a fixed point on the Earth’s surface [10], as is the case in INS/TACAN/ALT system. TACAN provides for measurements of distance D between the aircraft onboard equipment and the ground station as well as the azimuth θ of aircraft with respect to the ground station. The altimeter (ALT) provides for the altitude H of aircraft above the horizontal plane OXY. The geometric relationship between the measurements and the position of aircraft is illustrated in Fig. 2. As can be seen from Fig. 2, the relationship between the altitude H and the coordinate z is linear, whereas the distance D between the TACAN ground station and the on-board TACAN equipment, as well as the aircraft azimuth θ measured by TACAN are non-linearly related to the aircraft coordinates of position: This non-linear relationship leads to a nonlinear observation model of the system which breaches the linearity assumption of the Kalman filter [1, 2, 8]. Therefore, a Kalman filter with linearization of the observation model has been applied in the presented system. The filter is linearized around the reference trajectory (xˆ, yˆ, zˆ), which comes from the INS output (x, y, z)INS, corrected with the most recent estimates of INS positioning errors (δxˆ,δyˆ,δzˆ). Hence, the filter belongs to a category of extended Kalman filters (EKF) [1, 8]. The name of the filter, i.e. Complementary Extended Kalman Filter (CEKF), reflects the above mentioned fact, as well as the fact that the filter exploits complementary statistical features of INS and TACAN/ALT errors to derive its estimates of INS errors. Two additional blocks in Fig. 1, and h(*), represent transformation of INS errors from NED to ENU frame of reference [2] and calculation of distance D, azimuth θ and altitude H on the basis of INS-derived user position. Model of systemThe dynamics model of the designed system describes time propagation of INS errors. Detailed INS errors models can be very complicated and may contain even several tens of states [9, 10]. However, some of the states are observable only conditionally, e.g. during manoeuvres of the aircraft, and only in high quality inertial systems [10]. Moreover, elimination of chosen states does not conspicuously affect the accuracy of integrated system, but it significantly reduces requirements with respect to the processing power of the navigation processor. Simple 9-state model of INS errors can be used in practice [1, 9], and in this design it has been further simplified to 8-state model [3]. In spite of significant simplifications, the assumed INS errors model is still applicable, especially for aircraft that do not perform rapid turns around its pitch and roll axis. The proposed dynamics model is linear, which well suits the requirements of conventional Kalman filters. The discrete dynamics model of INS/TACAN/ALT positioning system is as follows:
As has already been mentioned, the non-linear relationship between measurements and user position leads to a non-linear observation model of the system. It can be linearized around the corrected INS trajectory, and the following equation, representing linearized measurement model, can be formulated
The above model has become the basis in designing CEKF for the INS/TACAN/ALT integrated positioning system. The detailed equations of the CEKF algorithm can be found in other papers of the author [5, 6]. |
||||||||
Pages: 1 2

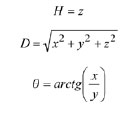
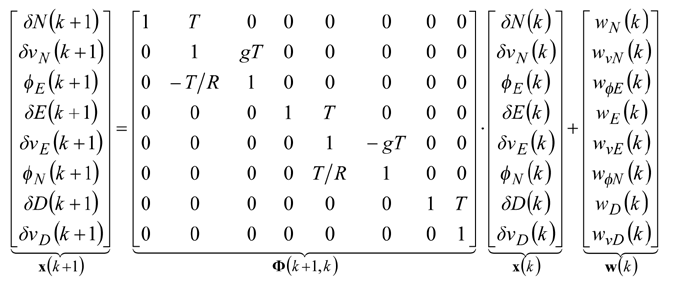
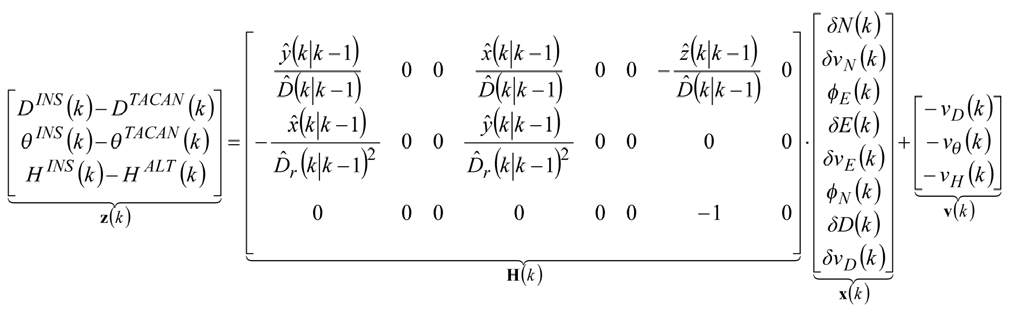










 (No Ratings Yet)
(No Ratings Yet)






Leave your response!