| Positioning | |
INS/TACAN/ALT- an alternative solution for positioning
|
||||||||
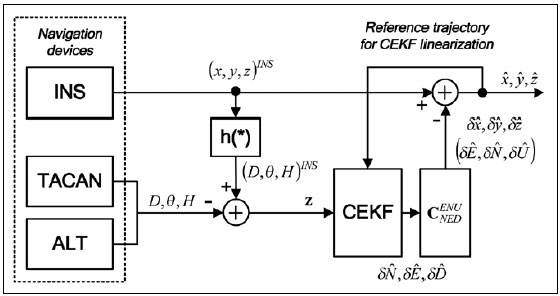
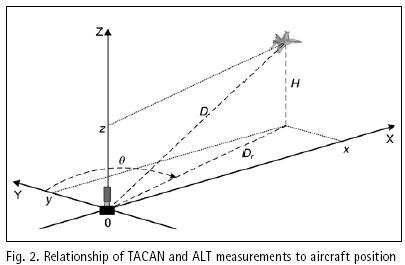
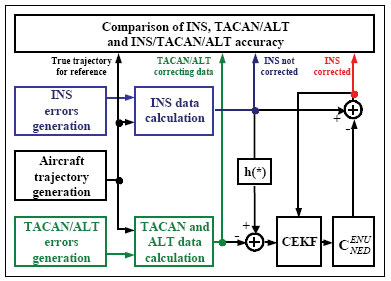
Structure and operation of systemThe system presented in the paper is designed according to the scheme of compensation and processes navigation data with use of a Complementary Extended Kalman Filter (CEKF). The INS/TACAN/ALT system works with a feed-forward correction, i.e. there is no feedback to INS and its errors are corrected externally. The structure of system is shown in the Fig. 1. The INS contains accelerometers and gyros, enabling calculation of linear and angular displacement [2, 9, 10]. Velocity and position of the vehicle are obtained through initialized single and double integration of accelerations, previously transformed from the body frame to the navigation frame of reference [9, 10]. It is assumed here, that INS position (x, y, z)INS will be expressed in an Earth-fixed reference frame OXYZ, with its origin at the location of TACAN ground station and with axes coinciding with the axes of the local horizontal frame of reference ENU (East-North-Up). The assumed frame is suitable for short-range systems, containing a navigation device, which measurements are to be referenced to a fixed point on the Earth’s surface [10], as is the case in INS/TACAN/ALT system. TACAN provides for measurements of distance D between the aircraft onboard equipment and the ground station as well as the azimuth θ of aircraft with respect to the ground station. The altimeter (ALT) provides for the altitude H of aircraft above the horizontal plane OXY. The geometric relationship between the measurements and the position of aircraft is illustrated in Fig. 2. As can be seen from Fig. 2, the relationship between the altitude H and the coordinate z is linear, whereas the distance D between the TACAN ground station and the on-board TACAN equipment, as well as the aircraft azimuth θ measured by TACAN are non-linearly related to the aircraft coordinates of position: This non-linear relationship leads to a nonlinear observation model of the system which breaches the linearity assumption of the Kalman filter [1, 2, 8]. Therefore, a Kalman filter with linearization of the observation model has been applied in the presented system. The filter is linearized around the reference trajectory (xˆ, yˆ, zˆ), which comes from the INS output (x, y, z)INS, corrected with the most recent estimates of INS positioning errors (δxˆ,δyˆ,δzˆ). Hence, the filter belongs to a category of extended Kalman filters (EKF) [1, 8]. The name of the filter, i.e. Complementary Extended Kalman Filter (CEKF), reflects the above mentioned fact, as well as the fact that the filter exploits complementary statistical features of INS and TACAN/ALT errors to derive its estimates of INS errors. Two additional blocks in Fig. 1, and h(*), represent transformation of INS errors from NED to ENU frame of reference [2] and calculation of distance D, azimuth θ and altitude H on the basis of INS-derived user position. Model of systemThe dynamics model of the designed system describes time propagation of INS errors. Detailed INS errors models can be very complicated and may contain even several tens of states [9, 10]. However, some of the states are observable only conditionally, e.g. during manoeuvres of the aircraft, and only in high quality inertial systems [10]. Moreover, elimination of chosen states does not conspicuously affect the accuracy of integrated system, but it significantly reduces requirements with respect to the processing power of the navigation processor. Simple 9-state model of INS errors can be used in practice [1, 9], and in this design it has been further simplified to 8-state model [3]. In spite of significant simplifications, the assumed INS errors model is still applicable, especially for aircraft that do not perform rapid turns around its pitch and roll axis. The proposed dynamics model is linear, which well suits the requirements of conventional Kalman filters. The discrete dynamics model of INS/TACAN/ALT positioning system is as follows:
As has already been mentioned, the non-linear relationship between measurements and user position leads to a non-linear observation model of the system. It can be linearized around the corrected INS trajectory, and the following equation, representing linearized measurement model, can be formulated
The above model has become the basis in designing CEKF for the INS/TACAN/ALT integrated positioning system. The detailed equations of the CEKF algorithm can be found in other papers of the author [5, 6]. |
||||||||
Piotr Kaniewski
|
|||||||||||||||
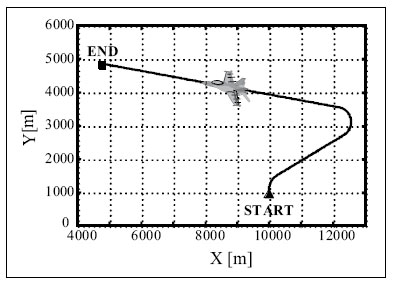
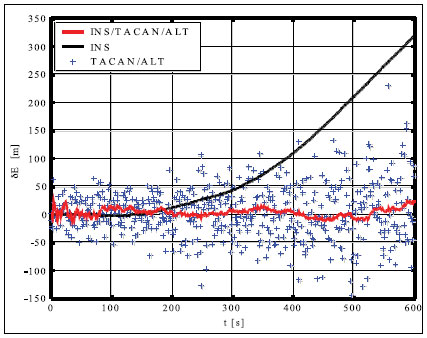
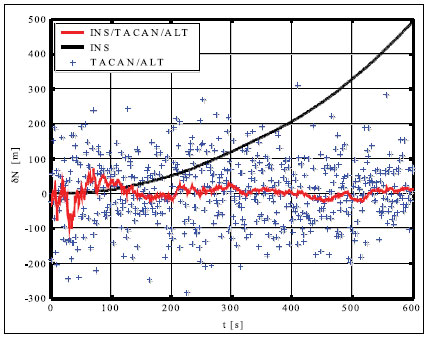
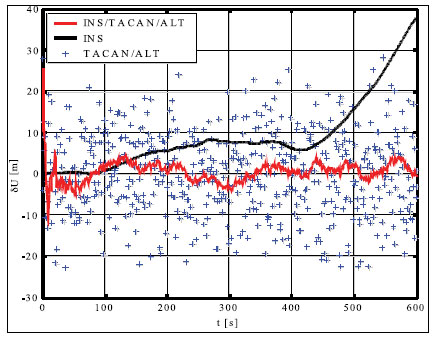
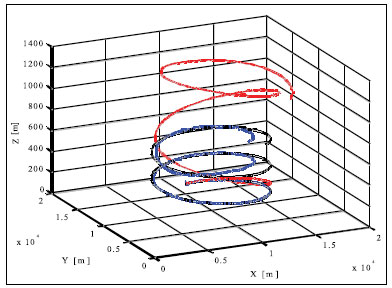
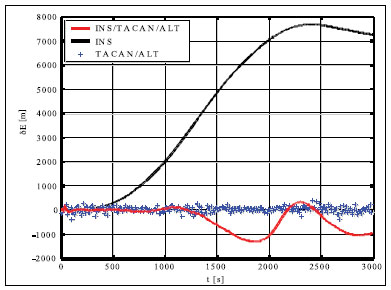
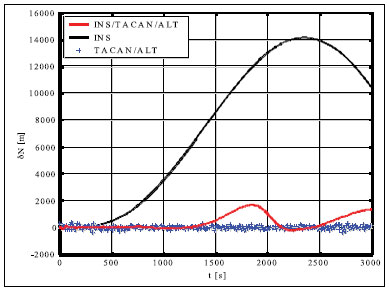
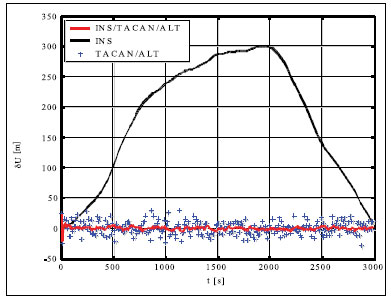
Simulation results and conclusionsThe designed positioning system has been tested via computer simulations. The simulations have included the following key steps: generation of aircraft trajectory, calculation of error-free values of distance Fig. 3. Methodology of simulations and azimuth and altitude of flight, generation of measurement errors, addition of error-free observables and their errors, joint processing of erroneous INS, TACAN and ALT data via CEKF. The methodology of testing is presented in Fig. 3. In the first scenario of simulations, lasting for 600 seconds, a horizontal path of flight, shown in Fig. 4, has been used. The altitude has been constant and equal 100 meters. Assumed standard deviations of TACAN distance and azimuth errors TACAN/ALT are presented in Fig. 5-7. From the above simulation results, one can see that INS/TACAN/ALT system is more accurate than any of its subsystems alone. The positioning errors of INS, increasing with the time of operation, have been eliminated and TACAN and ALT uncorrelated errors have been significantly reduced. One should be aware, however, Fig. 4. Horizontal path of flight used in first scenario of simulations that the system has an inherent drawback resulting from external INS correction. Along with time of operation, INS errors increase and so do the elements of measurement vector z. Then, the linearization of measurement model in CEKF introduces significant errors, which can even cause divergence of the filter. Fig. 5. Positioning errors – X (East) axis Fig. 6. Positioning errors – Y (North) axis Fig. 7. Positioning errors – Z (Up) axis This can be a serious problem especially in systems with low-grade inertial systems, especially if they are intended to operate uninterruptedly for long periods. Divergence of the estimated aircraft trajectory from the true trajectory in an INS/TACAN/ALT system with a lowgrade INS is demonstrated in Fig. 8. These results have been obtained for the second scenario of simulations, lasting for 3000 seconds. The assumed aircraft trajectory in this scenario represents an ascending spiral of radius 5000 m, starting at a point with coordinates: x = 10000 m, y = 15000 m, z = 100 m. As can be seen, the INS trajectory quickly diverges from the true trajectory of aircraft. As long as the distance between these two trajectories is not very large, CEKF is able to properly estimate INS errors and the estimated trajectory almost agrees Fig. 8. Aircraft trajectories in 2nd scenario of simulations: true (black), from INS (red), estimated (blue) Fig. 9. Positioning errors – X (East) axis Fig. 10. Positioning errors – Y (North) axis with the true one. After the first twist of the spiral, INS errors become too large for CEKF to properly estimate them, and the estimated trajectory goes away from the true one. This effect is further illustrated in Fig. 9-11, comparing positioning errors along individual axes of OXYZ frame of reference. One should note that the problem of divergence concerns only horizontal coordinates of position, as the vertical part of observation model is linear and does not require any linearization. The above demonstrated problem of divergence in INS/TACAN/ALT positioning system does not make the open-loop configuration useless, but imposes limitations on times of operation and requirements with respect to INS accuracy. The time of uninterrupted operation of the system without divergence is dependent on the quality of INS used in the system. As times of flight of aircraft are usually relatively short, the presented system can find its applications in aviation. Nonetheless, the author has recently designed a modified, closed-loop version of INS/TACAN/ALT system, which is able to operate long without divergence even with a low-grade INS. The new system will be shortly presented in another paper. As TACAN is a military system, the presented design is naturally dedicated for military aircraft. However, a slightly modified version of the presented system, with a pair of radiotechnical systems VOR/DME [7, 11, 12] instead of TACAN, can also be applied in civilian aircraft. VOR and DME systems are commonly used in civilian aviation and together they have functionality similar to TACAN. Maritime applications of the presented system are also possible. Fig. 11. Positioning errors – Z (Up) axis AcknowledgementsThis work was supported by the Polish Ministry of Science and Higher Education from sources for science in the years 2007-2010 under Commissioned Research Project PBZ-MNiSW-DBO-04/I/2007. References1. R.G. Brown, P.Y.C. Hwang, Introduction to random signals and applied Kalman filtering, John Wiley & Sons, Inc., USA, 1997. 2. M.S. Grewal, L.R. Weill, A.P. Andrews, Global Positioning Systems, Inertial Navigation and Integration, John Wiley & Sons, Inc., USA, 2001. 3. P. Kaniewski, Aircraft Positioning with INS/GNSS Integrated System, Molecular and Quantum Acoustics Vol. 27, 2006, pp. 149-168. 4. P. Kaniewski, Application of Unscented Kalman Filter in TACAN/ALT Integrated Navigation System, ENC-GNSS 2007, Geneva, Switzerland, 2007, CD. 5. P. Kaniewski: Integration of INS with TACAN and ALTIMETER, Molecular and Quantum Acoustics Vol. 28, Gliwice, 2007, s. 165-177. 6. P. Kaniewski: Aircraft Positioning with INS/ TACAN/ALT Integrated System, ENC-GNSS 2008 – The European Navigation Conference, Francja, Tuluza, 23-25.04.2008, DVD. 7. M. Kayton, W.R. Fried, Avionics Navigation Systems, John Wiley & Sons, USA, 1997. 8. G. Minkler, J. Minkler, Theory and Application of Kalman Filtering, Magellan Book Company, USA, 1993. 9. O. Salychev, Inertial Systems in Navigation and Geophysics, Bauman MSTU Press, Russia, 1998. 10. D.H. Titterton, J.L. Weston, Strapdown Inertial Navigation Technology – 2nd Edition, American Institute of Aeronautics and Astronautics, 2004. 11. U.S. Department of Transportation, U.S. Department of Defense, 2001 Federal Radionavigation Plan, DOT-VNTSCRSPA- 01-3/DoD-4650.5, USA, 2001. 12. U.S. Department of Transportation, U.S. Department of Defense, 2001 Federal Radionavigation Systems, DOT-VNTSCRSPA- 01-3.1/DOD-4650.5, USA, 2001. |
|||||||||||||||
|
|||||||||||||||
|
Pages: 1 2

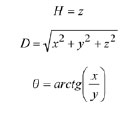
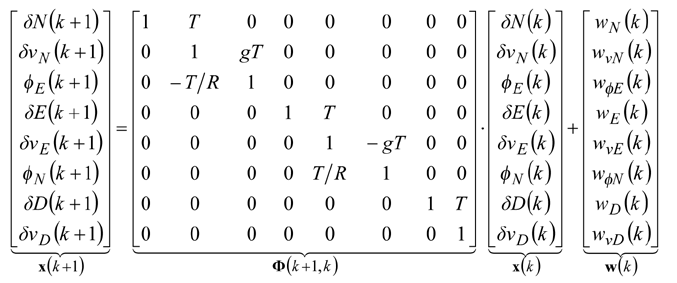
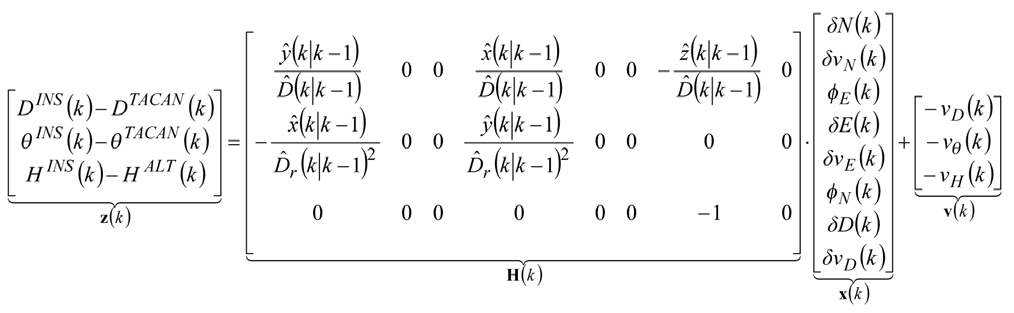











 (No Ratings Yet)
(No Ratings Yet)





Leave your response!