Fuzzy logic approach for sustainable land use planning

It is multi-objective in the sense one has to perform site suitability analysis for multiple objectives, which include agro-forestry, silvipasture, etc. Multiple criteria like land use, slope, soil, landform, groundwater prospects, etc, are involved in analyzing each objective. Similarly for generation of water resource action plan one has to perform site suitability analysis for check dam, percolation tank, stop dam, gully plug etc. Though the same problem can be broken into several single objective multi criteria decision-making problem, the procedure is going to be tedious.

Multi criteria decision making (MCDM)

Multi criteria decision-making (MCDM) problems involve a set of alternatives that are evaluated on the basis of a set of evaluation criteria (Malczewski 1999). The objective of using MCDM is to help find solutions to decision problems characterized by multiplechoice alternatives, which can be evaluated by means of performance characteristics called decision criteria.

Alternate approaches to GIS-based multi criteria analysis have been suggested to overcome the problem of weighting and data integration. Combining different factors, some exclusionary and some expedient, requires a weighting factor. Analytic Hierarchy Process (AHP) is an approach that can be used to determine the relative importance of a set of activities or criteria (Saaty 1990). AHP is a technique introduced by Saaty and has been widely used in the multi-criteria decision-making process in varied fields (Saaty and Vargas, 1990). Analytic Hierarchy Process (AHP) has been identified as a weighting strategy and Compromise Programming (CP) technique has been identified for data integration (Novaline et al. 1996, Deekshatulu et al. 1999).

Multi-Objective Multi-Criteria Decision- Making method Combination of Analytical Hierarchy Process and Compromise Programming techniques worked well in solving Single Objective Multi-Criteria problems like Site Selection for Water Harvesting Structure, Landslide Hazard Zonation (Novaline et al. 2001). But such a combination cannot be effectively used for solving Multi-Objective Multi- Criteria problems. Though the Multi-Objective Multi-Criteria Decision-Making problem can be broken into several single objective multi criteria decision making problem, solving this problem by applying combination of Analytical Hierarchy Process and Compromise Programming techniques is not going to be straight forward and effective. Moreover only absolute suitability within an objective can be addressed using MCDM techniques. In Multi-Objective Multi-Criteria Decision- Making problems, what is needed is the relative suitability for different objectives. In the present study we propose a Fuzzy classification approach in GIS for solving Multi-Objective Multi- Criteria Decision-Making problem.

Methodology

Fuzzy Classification in GIS

The fuzzy representation allows us to apply fuzzy techniques for geographical information processing (Burrough 1989). A fuzzy suitability rating method has been developed in this research. Compared with the conventional approaches, this method provides more information about land suitability. This approach not only solves a multi-objective multicriteria decision-making problem, but also overcomes the information loss seen in classical set theory-based decisionmaking (Novaline et al., 1997).

Highest Suitability (S1) – Lowest Suitability (S5)

If,

Ci = Representative Pattern Vector of

Class i

i = land use class

Ci = (Ci1, Ci2, Ci3,…..Cin) n = No.

of physiographical characteristics /

parameters

A = Area Vector

A generalized family of distance metrics, dependent on the exponent p, for

estimating the distance between Area Vector & Class pattern vector can be expressed as (Zeleny 1982, pp. 317) :

Where βj is the weight assigned to the parameter j and p ranges from 1 to α.

Varying p affects the relative contribution of individual deviations from the representative pattern vector, a greater emphasis being given to larger deviations as p tends towards a (Jose & Lucien, This distance metric as usually applied includes a sensitivity analysis for the three strategic values: p = 1,2 and a nominal a (i.e p > 10). When p = 1 (a ‘city block’ distance metric), total compensation between criteria is assumed, meaning that a decrease of one unit of one criterion can be totally compensated by an equivalent gain on any other criterion. For p = 2 (a straight line, Euclidean or the shortest distance metric) there is only partial compensation and p = a represents a totally non-compensatory situation (Zeleny 1982, pp.322-325). In the present implementation a value of 4 has been assigned to p after doing the sensitivity analysis for values between 1 and 10 for p. The smaller the distance, the more similar or suitable is the area to the land use class in terms of the land qualities.

In Conventional Classification, A e Ci, if dE(A,Ci) < distance to all other land use classes / Objectives.

This decision rule defines sharp decision surfaces between classes such that a vector can be classified into a single class and the classification implies a full membership in that class. Such a method is referred to as a hard partition of feature space.

The method developed in this research is characterized by a fuzzy partition of feature space. The fuzzy classification method enables one to rate an area’s suitability by comprehensively taking into consideration all its characteristics and all the land cover classes. An area can be classified into the most similar land cover class. However, the classical set theory-based decisionmaking leads to serious information loss. This can be explained by taking two areas as examples. In determining their suitability for a given crop, the distances from the vector of the first area to the four classes are 0.50, 0.40, 0.10 and 0.00 respectively. The distances from the vector of the second area to the classes are 0.90, 0.10, 0.00 and 0.00. According to conventional classification, both areas should be classified into class 1. But, clearly the first area is much less suitable for the crop than the second area. The information contained in the distances is discarded when the area’s memberships are determined. To make fuller use of the information, a fuzzy partition of feature space can be used. This method helps to suggest first best crop/land use, second best crop/ land use and so on for the same area.

In a fuzzy partition, the classes are defined as fuzzy sets. An area can be associated with partial membership and belong to different classes to different extents. A fuzzy set is characterized by its membership function. We define membership function fc for land use class c as, In Fuzzy Classification,

fci(A) – Membership function fc for land

use class Ci

m – no. of classes

m

Σ dE(A,Ci) serves as a normalizing

i=1 factor.

For a given area, membership functions are defined for each land use class. By calculating the functions, each area will have membership grades to all the land use classes, indicating the extent to which this area belongs to each of the land use class.

In case, the physiographical characteristics of an area are equal to those of the representative vector of suitability class C, that is

dE(A,Ci) = 0,

the membership grade of the area in class C is defined as 1 and the grades in other classes as 0s. This implies that this area can be exactly categorized into class C. Steps Involved:

Step 1: Normalize the Area values and Pattern Vector values for each class

Step 2: Compute the distance between Pattern Vector and Area Vector

Step 3: Convert the distances into Partial Membership functions.

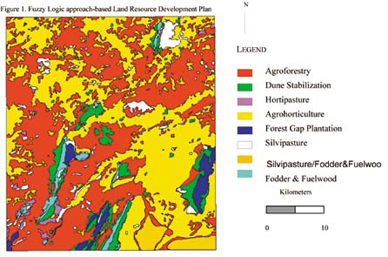
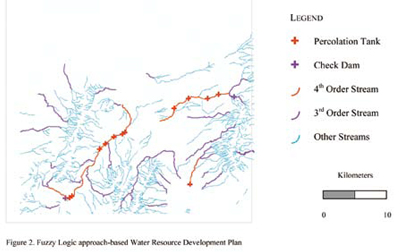
Implementation

The model was implemented using ARC/INFO GIS software. Arc Macro Language was used to program. Two problems were addressed:

1) Generation of Land Resource Action Plan

2) Generation of Water Resource Action Plan.

Land Suitability Analysis adopting fuzzy logic was done for ten land use classes, which were transformed into ten objectives. They include Silvipasture, Agroforestry, Forest Gap plantation, Fuel and fodder wood species, Hortipasture, Agro-horticulture, Forest enrichment, Forest protection & conservation, Horticulture and Dune Stabilization. Five terrain-related criteria namely, existing land use, soil, groundwater prospects, landform and slope were used and were analyzed within the AHP framework and were given importance in the order listed.

As one has to suggest suitable sites for water harvesting structures like check dams, percolation ponds, farm ponds, gully plugs for arresting soil erosion etc, the problem tends to be multi-objective as in the case of land resource action plan. So this also can be formulated using fuzzy suitability rating method. There were four objectives i.e finding suitable sites for percolation tank, check dam, gully plug and stop dam. Six terrain-related criteria namely, presence of lineaments, existing land use, slope, landform, ground water prospects and soil were used and given importance in the order listed. For land resource development plan generation, existing land use was given higher importance, because the new land use that would be suggested, should be similar to the existing land use as people might not accept total deviation from existing land use. Soil was given next preference, as the soil conditions should support the new land use, followed by groundwater prospects, landform and slope. Whereas, for water resource development plan generation, lineaments were given higher importance, to facilitate water percolation so that groundwater is recharged. Land use was given next preference, as the developed water resource would be utilized for the land use class, which requires increased water supply. This is followed by slope and landform, which offer varying degrees of terrain restrictions for water harvesting structures. And also, water harvesting structures become essential wherever groundwater prospects are poor. Soil is being given the least preference as its effective depth is negligible and therefore its influence on site suitability for water harvesting structures is less.

Modeling was done in raster environment. Vector data layers corresponding to various themes like land use, soil, groundwater prospects, landform, slope, lineament for a part of desert-prone district in Rajathan were used in the model. The importance values assigned to the parameters become the ß values in the distance equation (1). Decision Rules were framed by the resource experts for each objective (table-1). Highest suitability pattern vector (S1) represents ideal terrain conditions and always takes the highest value of 100. Terrain conditions represented by next highest suitability pattern vector S2, takes a value of 80 and so on and the Lowest suitability pattern vector S5, takes a value of 20. Terrain conditions in each cell (Area vector) were checked against the Ideal terrain conditions (Highest Suitability Pattern vector in table-1) for each objective and distance between these two vectors were found. The cell is assigned to that land use class for which the distance is closest, and therefore the membership grade is highest. Other membership grades for each cell is preserved in the database for finding the second best suitable land use or third best suitable land use. Therefore, one could get first best alternative, second best alternative etc. and there by generate different scenarios. Second best and third best alternatives become important when there is more competition for the first best alternative, which in turn would bring down its demand.

Conclusion

Conventional land assessment techniques are hampered by the inherent constraint of classical set theory that does not allow for partial set membership conditions and imprecise information. Consequently, one’s ability to use GIS, with conventional techniques, is severely limited. In contrast, fuzzy techniques are shown to reduce information loss by obtaining membership grades for each land suitability class. Such information allows identification of the extent to which a particular area belongs to a land cover class. It is also possible to use the stored fuzzy membership grades for database queries like.

– Find the second most suitable land use/crop for a particular area List all the areas, which are suitable for both agro-forestry and horticulture and find the suitability value.

– List all the areas, which are suitable for agro-forestry or horticulture and find the suitability value. Achieving greater balance between land use and land conditions should become more feasible through implementation of the methodology described here

References

Burrough, P. A., 1989, Fuzzy mathematical methods for soil survey and land evaluation. Journal of Soil Science, 40, 477.

Deekshatulu, B L., Krishnan, R., and Novaline, J., 1999, Spatial Analysis and Modelling Techniques – A Review. Proceedings of Geoinformatics – Beyond 2000 conference, Organized by Indian Institute of Remote Sensing, Dehra Dun, India, 268-275.

Jose, M.C.P., & Lucien, D., 1993, A Multiple Criteria Decision- Making approach to GIS-based Land Suitability Evaluation. International Journal of Geographic Information Systems, Vol. 7, No. 5, 407 – 424.

Malczewski, J., 1999, GIS and Multicriteria Decision Analysis. John Wiley & Sons,. Inc.

Novaline, J., and Saibaba, J., 1996, Enhancing the decision-making capabilities of GIS by adding Specialised tools. Proceedings of Geomatics conference, Published by Indian Institute of Remote Sensing (1996), DehraDun, India.

Novaline, J., and Saibaba, J., 1997, GIS & Analytical Modelling technique for sustainable development. In Geographic Information System and Remote Sensing Applications, edited by I .V. Muralikrishna (Allied Publishers Ltd. : India), pp. 509 – 514.

Novaline, J., Saibaba, J., Prasada, R., Krishnan, R., and Subramanian, S.K., 2001, Site selection for water harvesting structure in watershed development using DecisionSpace. Proceedings of Geomatics – 2001 conference, Organized by Indian Institute of Remote Sensing, Dehra Dun, India, 45-49.

Saaty, T.L., 1990, How to make a decision: The Analytic Hierarchy Process. European Journal of Operational Research, volume.48, 9-26.

Saaty, T.L., and Vargas L.G., 1990, Logic of Priorities. International series in Management Science / Operations Research, Kluwer Nijhoff Publishing, Boston / The Hague / London.

Zeleny, M., 1982, Multiple Criteria Decision Making, New York : Mc Graw – Hill.