| Geodesy | |
Determination of local gravimetric geoid
|
||||
|
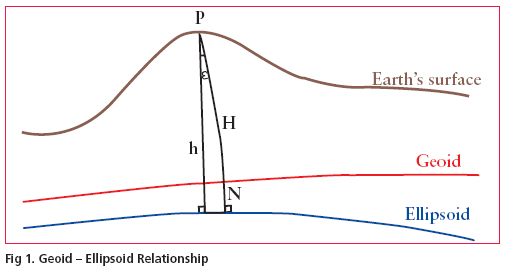
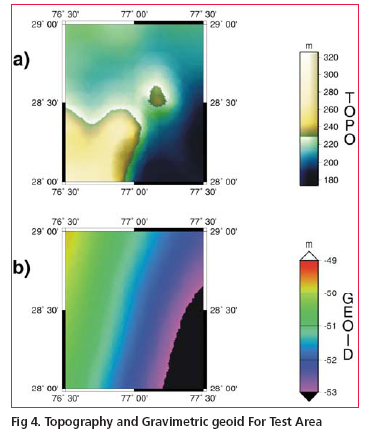
The demand for a high resolution geoid model has grown substantially during the last few decades especially after inception of Global Positioning System (GPS). Many countries across the world have already developed their own geoidal model which serve as the means of deriving orthometric heights from GPS observations. The impact of GPS on surveying application is undeniable. More so, this revolution has not been confi ned to the surveying community, but has extended into mapping, navigation and Geographic information system (GIS) areas. During the last few years, we have been witnessing the wide spread adoption of GPS with an equivalently vibrant range of accuracy requirement. Many of these applications require accurate vertical positions. The task of transforming the ellipsoidal height obtained from GPS technique to the orthometric height has prompted geodesists around the world to determine the high precision geoid undulations, for their region of interest. In India the present day nation wide geoid was computed a long time back and based on astro geodetic observations with respect to Everest spheroid. It has various limitations and does not have any signifi cance as far as GPS solutions for orthometric height is concerned. Present study was taken up to validate the results of orthometrc heights derivation in a pilot project of large scale mapping of a part of Delhi through Airborne Laser Terrain Mapping(ALTM) Technique. A fairly dense gravity anomaly data consisting of about 160 uniformly distributed points covering a block of 1° X 1° including National Capital Region(NCR) of Delhi was used in the geoidal modelling process .The study was aimed at to analyse approach of data preparation and treatment procedures and a evaluation of test results obtained from the analytical solution of Stokes’ integral with appropriate Kernel modifi cations. Gravimetric Geoid and GPSThe geoid can be broadly defi ned an equipotential surface of Earth’s gravity fi eld that closely approximates with mean sea level (MSL) neglecting long term effect of sea surface topography (SST). The fundamental relationship between the geoid and The geoid undulations (N) may be computed in a simple manner by doing GPS observations in order to determine the ellipsoidal heights at all levelling bench marks. However if heights of some other points is required to be given it may not be possible to extrapolate the GPS- levelling heights differences. In this case gravimetric information may be used to bridge the gap through determination of local gravimetric geoid. In a broad sense geoidal surface is that undulating surface along which the potential remains the same.The undulations of the geoid are not the same as, but are affected by the variations in topography. Because of this complexity, high resolution gravimetric geoid models and associated interpolations software have been developed to support GPS height conversion. |
||||
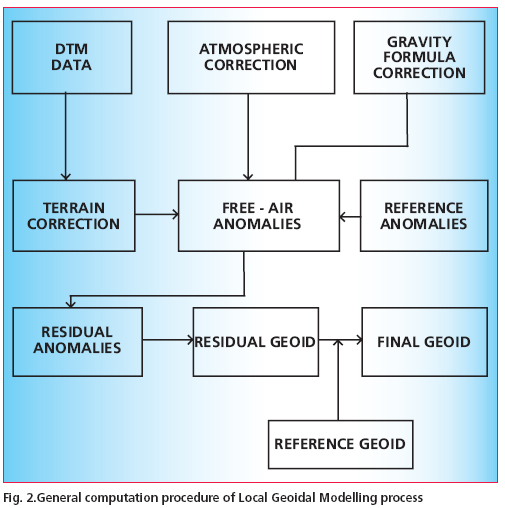
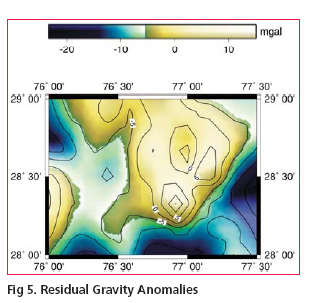
Data preparationFree air gravity anomoly data The converted values were used in subsequent computations of geoid model. Digitial elevation model for terrain correction MethodologyThe methodology for geoid computation was based on remove –compute– restore technique as described in sec.2. and can be summarized as follows: Computation of geoidal height at a given point with respect to EGM96 (NEGM96) is quite simple using the EGM96 spherical harmonic potential Coeffi cient set and spherical harmonic correction coeffi cient both complete to degree and order 360. However the procedure for computation of indirect effect from local topography(NRTM) |
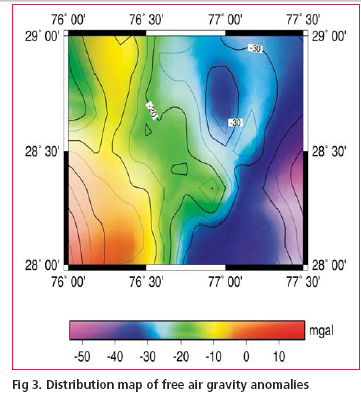
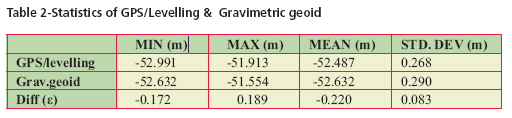
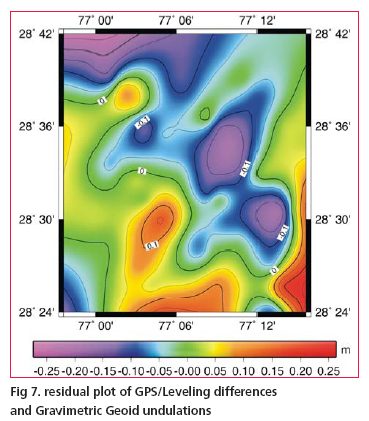
Evaluation of Geoid ModelDifferences between the GPS derived ellipsoidal heights and the levelling heights of bench mark of national control network are generally being used for geoid evaluation. In present study the GPS/levelling differences were derived by making GPS observations on 50 nos. of stations and connecting them to bench marks of Indian vertical control network by running precision leveling lines. GPS data was processed using BERNESE Software Ver.4.2 and an accuracy of derived ellipsoidal height of the order of few cm has been achieved. None of these stations was included in the geoid modeling process. The quantities to compare are the geoidal heights from the gravimetric geoid Ngrav and the corresponding geoidal height NGPS from GPS/leveling observations. The misfi t ε ε = NGPS – Ngrav includes datum differences, systematic errors and subsidence /uplift in the levelling, as well as errors in the gravimetric geoid. The statistics of the GPS/levelling differences and heights from gravimetric geoidal model have been presented in Table 2 and Fig. 7 shows the contour plot of the differences. The above results clearly show a close matching between the gravimetric geoid and GPS/leveling differences and probably described the advantage of using dense gravity data. There is hardly any longitudinal variations noticed for the geoid but it has shown the traces of northward gradual slope which may be evident more clearly when computations are taken for a larger region. Though the results still contain the systematic differences between local levelling network and the gravimetric geoid but major contribution of these errors has been nullified due to the fact that test area is considerably small and terrain effect is almost negligible because of smooth topography of the region. ConclusionsThis paper has described a brief review of some of the important aspects involved in computation of gravimetric geoid model in Indian context. The use of generalized scheme along with modifi ed Stokes Kernel in remove-compute-restore technique has been successful to a great extent in computation of geoid model from dense gravity anomaly data of Delhi area. The study has fi rmly shown that EGM96 can be effectively used for gravimetric geoidal modeling in India notwithstanding its own shortcomings provided that the other aspects of the methodology are explicitly designed and followed carefully. The procedure of analytical solution of Stokes integrations with spherical cap of radius of o.5° using dense gravity data has worked well and achieved an accuracy, in absolute sense, of the order of 20 cm as determined from comparison with GPS/leveling differences making it an alternative to conventional method of leveling, suitable for most of the mapping applications. However a signifi cant size of errors in GPS determined ellipsoidal heights is always expected from the various error sources. Even with a very detailed error modeling of all the possible source effects the achievable accuracy of GPS ellipsoidal height is always considered to be less than the horizontal positional accuracy. Hence the extent of misfit between the gravimetric geoid and GPS/levelling difference should not be always viewed entirely due to error in gravity measurements or inadequate geoidal modelling procedure. AcknowledgementsThe authors gratefully acknowledge the consistent effort made by officers and staff of satellite geodesy and project survey wings of G&RB for their excellent work of field data collection, processing and typing of this manuscript. ReferencesBurrared, S.G.,1910, Levelling of Precision in India, GTS Vol. XIX, Survey of India, Dehradun Forsberg ,R.(1994) Terrain effects in Geoid computation, Lecture notes, Int. school for the determination and use of geoid, Milano. Heiskanen, W,Moritz , H (1967) Physical Geodesy, Freeman, San Fransisco. Lemoine FG, Smith D, Smith R, Kunz L, Pavlis E, Pavlis N, Klosko S, Chinn D, Torrence M,Williomson R, Cox C, Rachlin K, Wang Y, Kenyon S, Salman R, Trimmer R, Rapp R, Nerem S (1996) The development of NASA GSFC and DMA joint Geopotential model, Proc. of International Symposium on Gravity Geoid and Marine Geodesy, University of Tokyo. Morelli C,Gantar C,Honcaslo T,Mc connel RK,Tanner TG,Szabo B,Uotila,U,Whalen CT(1971) The International Gravity Standardisation Network(IGSN71),Bull Schwarz K.P., Sideris M.G. and Forsberg R. (1990).The uses of FFT techniques in Physical Geodesy. Geophysical J. Int, pp.485-514. Vanicek P , Sjöberg LE(1991) Reformulation of Stokes’ theory for higher than second-degree reference fi eld and modifi cation of integration kernels,J. Geophys. Res. 96(B4):6529-6540. |
||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||
|

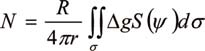 (1)
(1)














 (No Ratings Yet)
(No Ratings Yet)





