Determination of local gravimetric geoid
Feb 2007 | Comments Off on Determination of local gravimetric geoid
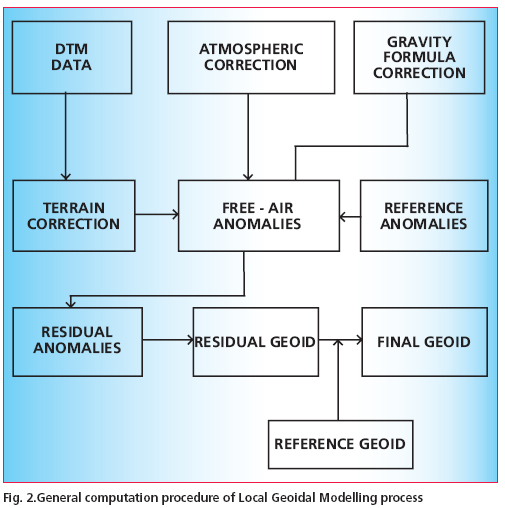
Geoid computation procedure
The geoid determination process employed Stokes’ integral formulae which allows a pointwise calculation of gravity fi eld quantities and thus provide the possibility of an arbitrarily high gravity fi eld resolution which depends only on data coverage and quality. Utilizing local gravity anomalies as the primary data set classical solutions is aimed at the determination of geoid height.
Purely gravimetric calculations of geoid heights is hampered by longwave systematic data errors and by inhomogeneous spatial resolutions and accuracy of the local gravity data. The global geopotential models such as EGM96( Lemoine et.al.,1998) generally provides the long wave part of the gravity fi eld and dense local gravity data together with highresolutions digital elevation models leads to a combined solution that can be applicable to a limited region, where data smoothening techniques are used by considering the terrain effect. A remove compute- restore technique(Schwarz et.al.,1990) is applied in this study which includes the following steps.
1. Calculation of necessary corrections e.g. gravity formula corrections for free-air anomalies data to obtain corrected gravity anomalies Δgcor
2. Reduction of the gravity anomaliesΔgcor by the anomaly part of the global model to a degree of expansions m and obtain the reduced anomalies Δgm
3. Smoothening of the anomalies by applying the terrain corrections Δgt.
4. Griddings of the residual gravity anomalies
Δgres = Δg – Δgcor – Δgm – Δgt
5. Application of Stokes formula on the residual gravity anomalies resulting on residual geoid heights Nres
6. Restoration of the effect of the global model and the terrain to the residual geoid heights:
N= Nres +Nm +Nt
A schematic diagram of the general computation procedure is given in figure 2.
Stokes Integration:
The Stokes integral is one of the fundamental and most important formulae in physical geodesy. It was derived by G.G. Stokes in 1849 to compute geoid undulations N from terrestrial gravity anomalies (Heiskanen and Moritz, 1967) :
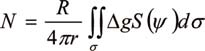 (1) (1)
Where R Mean earth radius
γ Mean normal gravity for the earth
σ The sphere of integrations
S(ψ) Stokes` function
Δg Free air gravity anomalies dσ Element of surface area on the sphereΨ Surface spherical radius (ψ) between two point on the sphere and is given by
cosψ = sinΦ sinΦ` + cosΦ
cosΦ` cos(λ` – λ)
Where Φ,λ are geographical coordinates of computation point and Φ`and λ` are the coordinates of surface element dσ. The Stokes` function in closed form is defi ned as,
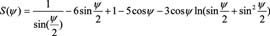 (2) (2)
The Stokes` formula in its original form suppresses the harmonic terms of degrees one and zero in N and it holds only for a reference ellipsoid that;
(1) Has the same potential as the geoid.
(2) Encloses a mass that is numerically equal to earth’s mass.
(3) Has its centre at the centre of gravity of the earth.
|
| |
«Previous 1 2 3 4 5View All| Next»
Pages: 1 2 3 4 5






 (5.00 out of 5)
(5.00 out of 5)





 (5.00 out of 5)
(5.00 out of 5)





 (5.00 out of 5)
(5.00 out of 5)





 (5.00 out of 5)
(5.00 out of 5)