Determination of local gravimetric geoid

Data preparation

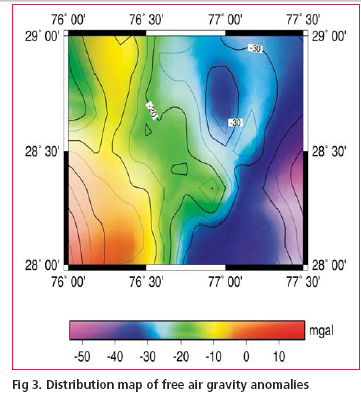
Free air gravity anomoly data
Free air anomaly values of test area were compiled from observed gravity database maintained by Geodetic & Research Branch (G&RB) , Survey of India. The compiled data base comprised of about 160 gravity values spread uniformly over the test area (see fi g.3). The datum for all Indian gravity measurement is a network of local base stations which were tied to the International gravity standardization Network 1971 (Morelli et. al. 1971). It is not known whether any variant of the tidal correction was applied to the local gravity observation and also the given elevations of gravity stations
were of variable quality. Some of the gravity observations were done on benchmarks of Indian levelling network whereas for a large portion of gravity stations the elevations were computed based on barometric levelling which can be in error of the order of ±2 – 4 m. Since the gravity anomalies values were based on International Gravity formula (1967) therefore to bring them in the Geodetic Reference System 1980 (GRS80) the following transformation was applied (NGS, 1986).
Δg1980 = Δg1967 – (0.8316 + 0.0782 sin2Ø – 0.0007 sin4Ø)

The converted values were used in subsequent computations of geoid model.

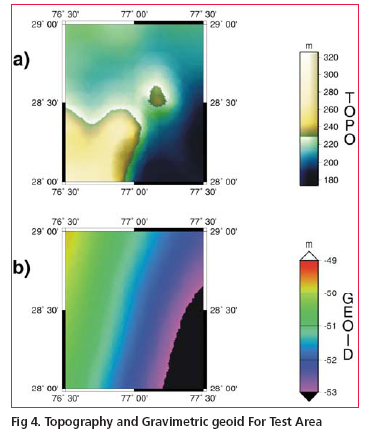
Digitial elevation model for terrain correction
Since as on today no nationwide digitial elevation model (DEM) on appropriate scale is available, a local DEM was computed based on about 130 spot heights in the area. These elevation data have been gridded by using least square collocation (LSC) technique with second order Markov covariance function(Fig.4(a)). The DEM was generated in a grid of 15 X 15 arc second and tested for observed heights versus the interpolated heights. In general these spot heights were found to be in good agreement with the interpolated DEM heights.

Methodology

The methodology for geoid computation was based on remove –compute– restore technique as described in sec.2. and can be summarized as follows:
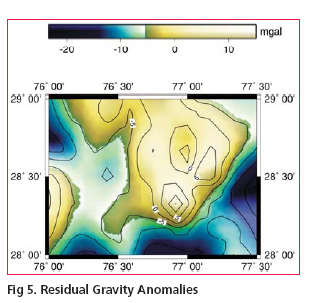
• Remove the long wave length part of EGM96 global geopotential model and terrain effect from the observed free air gravity anomalies to derive residual gravity anomalies(Fig.5).
• Compute the residual undulations NRES of the geoid by numerical integration of Stokes integral (Eqn.1) using reduced gravity anomaly data.
• Restore the long wavelength effect NEGM96 and residual terrain effect NRTM to get final geoidal undulation N that is:
N = NEGM96 + NRTM + NRES

Computation of geoidal height at a given point with respect to EGM96 (NEGM96) is quite simple using the EGM96 spherical harmonic potential Coeffi cient set and spherical harmonic correction coeffi cient both complete to degree and order 360. However the procedure for computation of indirect effect from local topography(NRTM)