Determination of local gravimetric geoid
Feb 2007 | Comments Off on Determination of local gravimetric geoid

and Residual undulation NRES using Stokes` integral is little complicated and required to be discussed in detail.
Terrain correction
Computation of NRTM is done relative to the mean elevation surface (fig.6) In case of remove – compute – restore technique, substracting the contribution of reference global geopotential model from the local terrestrial gravity data also include the effects of the global topography ; therefore substraction of further topographic effect may introduce long wave length effects into the residual potential. To avoid this only short wavelengths of the topographic effect may be used, which is termed as residual terrain model (RTM) effect(Forseberg,R,1994) . The RTM terrain effect may be computed in a spherical cap around the computation point, provided the cap is sufficiently large so that the remote residual topography has a negligible effect. In this study the mean elevation surface was determined from the DEM data by applying the moving average method. The RTM gravity terrain effect in the planner approximation given by a volume integral:
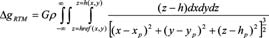 (3) (3)
Where h are the heights of topography, G is the gravitational constant andρ is the mass density taken as 2.67 gm/cm3 in the computation. The computations of ΔgRTM were done
in space domain prism integration by Fast Fourier Transform (FFT) method using the dense height data.
Modifi cation of kernel
Modifi cation of Kernel S (ψ) in Stokes` formula forms an important part of geoid determination process due to the fact that long wave-length systematic errors in gravity data can produce large geoid errors. These systematic errors can be avoided by modifying the classical Stokes` Kernel in an appropriate manner. There are different ways of modifi cations, however in our study we used the modifi cation suggested by Wong and Gore (1996).
As per the technique the spheroidal Stokes’ kernel S(ψ) in equation (1), which is implicit to the Stokes’ formula, can be modifi ed simply by removing the appropriate-degree Legendre polynomials [Pn(cosψ)] from the closed form of the spherical Stokes’ Kernel (Eqn.2).
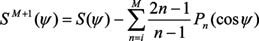 (4) (4)
Where is the spherical distance between the computation point and integration points. We may choose any degree of modifi cation to our choice which permits the ultimate geoid to best fi t the GPS-Levelling undulations. At the same time the
modifi cation approach should be applied in combination with capsize radius ψ = ψm as both the reference geoid EGM96 as well as local gravity data may have errors and therefore the difference between the two geoids i.e. gravimetric and GPS-Levelling with different degrees of modifi cations does not necessarily equal to zero.
Thus kernel modifi cation and capsize assumptions provide the means of optimising the solution of Stokes` integral in determination of local geoid.
Geoid model construction
For computation of geoid the degree of Kernel modifi cation in Eqn. (4) was chosen to be m=360, which is same as the degree of reference global geopotential model EGM96. Eqn. (1) when applied over a limited spherical cap of radius (ψ°=0.5°) about each computation
point leads to the following approximation of geoid height
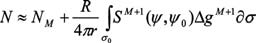 (5) (5)
The concept of spherical cap of limited spatial extent in analytical solutions of Stokes’ integration was implemented simply by setting the value of to zero out side the cap region. The fi nal geoid was constructed based on the methodology described in section 3. The reduced gravity data was arranged in a grid using Least Squares collocation (LSC) technique. Geoidal heights were computed by applying the generalized Stokes’ scheme(Eqn. 5) using spherical cap of radius 0.5°. NRTM was computed by planar approximation implemented using FFT technique on the 0.5 Km basic resolution grid. Finally, NEGM96 was added to NRES and NRTM to obtain the final geoid (Fig. 4(b)). Table 1 below shows the statistics of the various component computed at the different stages of the model construction Looking at the table-1 the effect of Residual terrain model (NRTM) is almost negligible and only shortwave residual gravity anomalies contributes to reference geoid i.e. EGM96. However the effect, as evident from the table-1 is order of 35-55 cm which is a minor quantity in comparison to the total geoidal undulation (≈- 53 m). Thus EGM96 geoid is very smooth in the region and almost fit in to the local geoid having only the minor short wave length variations.
|
| |
«Previous 1 2 3 4 5View All| Next»
Pages: 1 2 3 4 5






 (5.00 out of 5)
(5.00 out of 5)





 (5.00 out of 5)
(5.00 out of 5)





 (5.00 out of 5)
(5.00 out of 5)





 (5.00 out of 5)
(5.00 out of 5)