| Navigation | |
A new approach for SINS stationary self-alignment
|
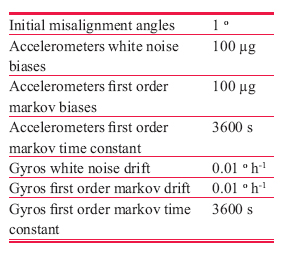
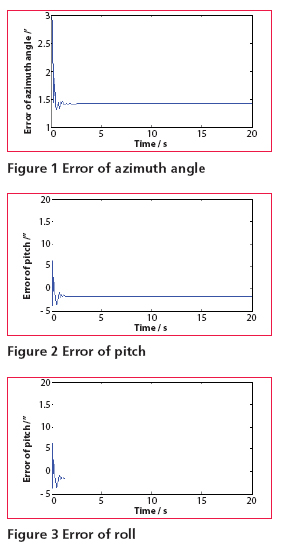
Then, combine (15) and (16), measurement equation can be written as Observability analysisThe accuracy and speed of alignment is decided by the performance of filter, which is decided by the observability of model. So the observability analysis of model must be performed before filter can commence. The SINS stationary alignment model established in this paper, is a linear time-invariant system whose observability can be obtained by the analysis of the observable matrix. The rank of the observable matrix is It shows that the model is complete observable. And the fi lter is capable of estimating the state with good performance, therefore, the model will lead to a high accuracy and speed of alignment. Modifi ed Sage-Husa adaptive Kalman filterSage-Husa adaptive Kalman fi lter algorithm proposed by Sage A P and Husa G W, is a fi lter algorithm which can estimate system noise and measurement noise online in real-time. However, the algorithm could run well under the unknown prior statistical characteristics circumstance. There are some problems with the algorithm, such as, 1) stability and astringency of measurement noise is poor, which affect stability of state estimation and fi lter result directly, 2) system noise and measurement noise can’t be obtained accuracy at the same time, 3) The minus operation would make the matrix of system noisy estimation and the matrix of measure noisy estimation lose half positive or positive, which will make the fi lter diverge. In order to solve the problems analyzed as above, a modified Sage-Husa adaptive Kalman filter algorithm is proposed as follow SimulationDuring the simulation, parameters of a medium accuracy IMU are used. Its details are shown as following. Simulation results are given in figures 1-6, which fi gures 1-3 are the errors of attitude angle and fi gures 4-6 show the estimation errors of gyro drift rate. Figures 1-6 show that the fi lter works well. After less than 5 s, it have already converged rapidly. According to the computer simulation results, the errors of the two leveling attitude angles are about 5 ‘’, and the error of the azimuth angle is about 1.5 ‘. Computer simulation results also verify that the optimal time of the three misalignment angles is less than 5 s. Figures 4-6 show that three gyros drift rate are estimated accurately. While the traditional initial alignment have the alignment accuracy of 10 ‘’ for leveling attitude angles and 2-5 ‘ for azimuth angle, with the alignment time of 20-50 s. ConclusionBecause of the poor observability of the system, it is hard to give attention to the accuracy and speed of alignment by the traditional initial alignment technology. In order to solve this problem, through analyzing the characteristic of the SINS stationary alignment seriously, a bran-new SINS stationary alignment approach is proposed by means of establishing new system model and measurement model. The new approach could complete the SINS stationary alignment process through the outputs of IMU without any external information. According to the observability analysis, |

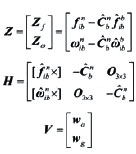

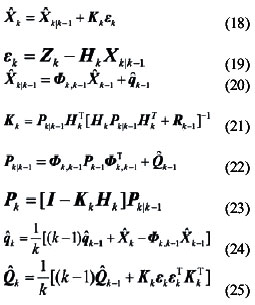










 (No Ratings Yet)
(No Ratings Yet)





