A new approach for SINS stationary self-alignment
Feb 2007 | Comments Off on A new approach for SINS stationary self-alignment
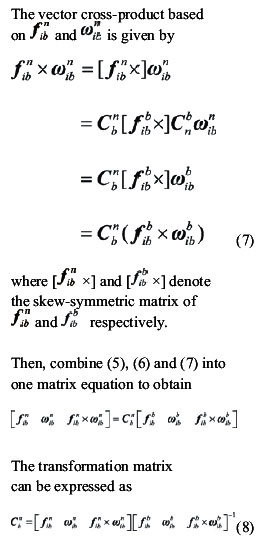
Equation (8) shows that the output of the accelerometers and gyros of a stationary SINS can be used to determine the attitude matrix directly.
Fine alignment
Coarse alignment is based on an idealization in which there are no accelerometer and gyro errors. But both accelerometers and gyros output data have errors in reality, especially the gyros may have large rate biases. So the attitude matrix given by coarse alignment may have some error. Now, using the notation  to denote the attitude matrix given by coarse alignment, and represent the ideal attitude matrix, the relationship to denote the attitude matrix given by coarse alignment, and represent the ideal attitude matrix, the relationship  between between and can be described as and can be described as

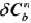 is caused by errors in the orientation of the body frame with respect to the navigation frame. In terms of small misalignment angles, is caused by errors in the orientation of the body frame with respect to the navigation frame. In terms of small misalignment angles,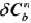 may be represented in the equivalent form of a skew-symmetric matrix may be represented in the equivalent form of a skew-symmetric matrix

where φ denote the vector of misalignment angles, namely,
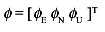
System equation
The mission of fi ne alignment is to obtain more accurate attitude matrix based on coarse alignment, that is, to estimate precise misalignment angles. In SINS stationary alignment, the misalignment angles remain constant, while no SINS navigation calculation is carried out. Then, the differential equations of misalignment angles can be written as
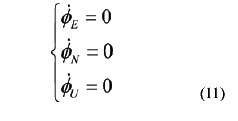
Besides to determine misalignment angles in the alignment, we also need to estimate the biases of accelerometers and gyros which would be used to compensate the output of IMU during navigation. Here, the biases of accelerometers and gyros are considered as some noise processes which are consist of first order Gauss-Markov noise and Gaussian white noise. Thus, the IMU error model is written as

Now, combine (11) and (13), system equation can be written as
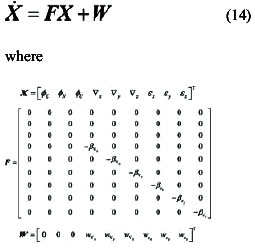
Measurement equation
Taking care of the error of accelerometers, (5) can be written as

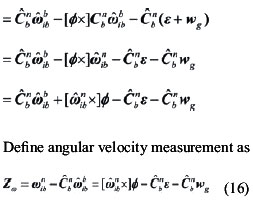
|
«Previous 1 2 3 4View All| Next»
Pages: 1 2 3 4






 (5.00 out of 5)
(5.00 out of 5)





 (5.00 out of 5)
(5.00 out of 5)





 (5.00 out of 5)
(5.00 out of 5)





 (5.00 out of 5)
(5.00 out of 5)