| Navigation | |
A new approach for SINS stationary self-alignment
|
||||
|
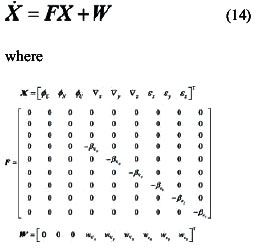
The object of the SINS selfalignment is to determine the direction cosine of the transformation from the body frame to the navigation frame, namely, the elements of initial attitude matrix, using the accelerometer and gyro outputs. As the alignment accuracy affects the accuracy of the navigation system directly, one of the most important requirements of SINS alignment is high alignment accuracy. In many practical At present, the alignment model given by Bar-Itzhack and Bermant with the observations of velocity, is widely used in general stationary SINS selfalignment, such as fast alignment proposed by Jiang Cheng Fang and De Jun Wan, multipositon alignment presented by Jang Gyu Lee, Chan Gook Park and Heung Won Park, while it is not completely observable. In this model the east gyro drift rate is only weakly coupled to the velocities which would serve as external information for the purpose of alignment. So it is hard to give more attention to alignment accuracy and alignment speed during stationary self-alignment using the traditional initial alignment methods. In this paper, a new self-alignment approach based on the measurement of IMU is proposed for SINS on a stationary base. The approach needn’t to carry out SINS navigation calculation, thereby, it breaks away from the model which is not completely observable. Meanwhile, it takes full advantage of specific force and angular velocity information.which is the sensed output of IMU as well as the characteristic of SINS stationary alignment. In order to make sure the high accuracy and speed of alignment, a new alignment model which is completely observable, is established for the approach. On the other hand, for the snake of selfalignment, IMU measurement is used as observations instead of velocities. The main work of this paper is following: firstly, coarse alignment algorithm is presented. Secondly, a new fi ne alignment model for SINS stationary self-alignment is derived, and the observability of the model is analysed. Then, a modifi ed Sage-Husa adaptive Kalman fi lter is introduced to estimate the misalignment angles. Finally, some computer simulation results illustrate the effi ciency of the new approach and its advantages, such as higher alignment accuracy, shorter alignment time, more selfcontained and less calculation. Coarse alignmentNormally, SINS initial alignment process is divided into two phases, i.e., coarse alignment and fi ne alignment. The purpose of coarse alignment is to provide a fairly good initial condition for the fi ne alignment processing. For SINS stationary alignment, the carrier is fi xed to the Earth. And some characteristics of stationary alignment are conclude as follow: where g and ωie represent the magnitude of gravity and Earth rate, respectively,ϕ is the local geographical latitude. For the SINS, the accelerometer and gyro output can be expressed respectively as |
||||
|
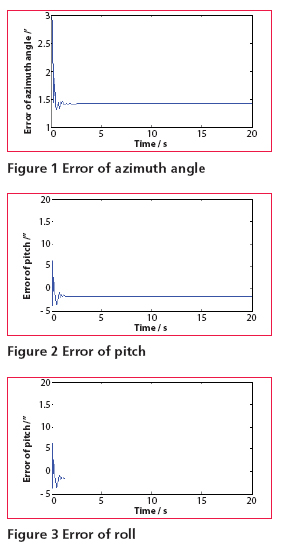
Then, combine (15) and (16), measurement equation can be written as Observability analysisThe accuracy and speed of alignment is decided by the performance of filter, which is decided by the observability of model. So the observability analysis of model must be performed before filter can commence. The SINS stationary alignment model established in this paper, is a linear time-invariant system whose observability can be obtained by the analysis of the observable matrix. The rank of the observable matrix is It shows that the model is complete observable. And the fi lter is capable of estimating the state with good performance, therefore, the model will lead to a high accuracy and speed of alignment. Modifi ed Sage-Husa adaptive Kalman filterSage-Husa adaptive Kalman fi lter algorithm proposed by Sage A P and Husa G W, is a fi lter algorithm which can estimate system noise and measurement noise online in real-time. However, the algorithm could run well under the unknown prior statistical characteristics circumstance. There are some problems with the algorithm, such as, 1) stability and astringency of measurement noise is poor, which affect stability of state estimation and fi lter result directly, 2) system noise and measurement noise can’t be obtained accuracy at the same time, 3) The minus operation would make the matrix of system noisy estimation and the matrix of measure noisy estimation lose half positive or positive, which will make the fi lter diverge. In order to solve the problems analyzed as above, a modified Sage-Husa adaptive Kalman filter algorithm is proposed as follow SimulationDuring the simulation, parameters of a medium accuracy IMU are used. Its details are shown as following. Simulation results are given in figures 1-6, which fi gures 1-3 are the errors of attitude angle and fi gures 4-6 show the estimation errors of gyro drift rate. Figures 1-6 show that the fi lter works well. After less than 5 s, it have already converged rapidly. According to the computer simulation results, the errors of the two leveling attitude angles are about 5 ‘’, and the error of the azimuth angle is about 1.5 ‘. Computer simulation results also verify that the optimal time of the three misalignment angles is less than 5 s. Figures 4-6 show that three gyros drift rate are estimated accurately. While the traditional initial alignment have the alignment accuracy of 10 ‘’ for leveling attitude angles and 2-5 ‘ for azimuth angle, with the alignment time of 20-50 s. ConclusionBecause of the poor observability of the system, it is hard to give attention to the accuracy and speed of alignment by the traditional initial alignment technology. In order to solve this problem, through analyzing the characteristic of the SINS stationary alignment seriously, a bran-new SINS stationary alignment approach is proposed by means of establishing new system model and measurement model. The new approach could complete the SINS stationary alignment process through the outputs of IMU without any external information. According to the observability analysis, |
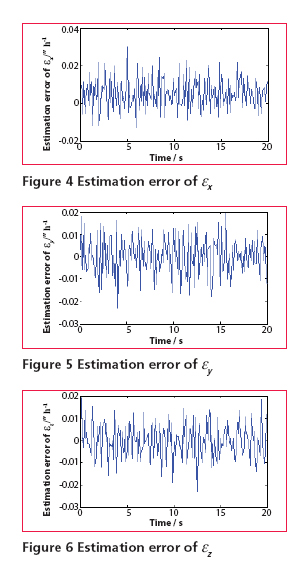
the alignment model established in this paper, is complete observable, which brings the excellent performance of the filter as well as the high accuracy and speed of the alignment. Compared with the traditional initial alignment technology, the new approach have such advantages as follow: it could estimate all states include east gyro drift rate and azimuth misalignment angle accurately in short time; higher alignment accurate; shorter alignment time; more self-contained and less calculation. Therefore, the new approach is a preferable choice for SINS stationary self-alignment. Reference[1] Bar-Itzhack I Y, Bermant N,“Control theoretic approach to inertial navigation systems”, AIAA Journal of Guidance, Control and Dynamics, 1988, Vo. 11, No. 3, pp. 237-245. [2] Goshen-Meskin D, Bar-Itzhack I Y, “Unified approach to inertial navigation system error modeling”, AIAA Journal of Guidance, Control and Dynamics, 1992, Vo. 15, No. 3, pp. 648-653. [3] YEON FUH JIANG, YU PING LIN, “Error Estimation of INS Ground Alignment Through Observability Analysis”, IEEE Transaction on Aerospace and Electronic Systems, 1992, Vo. 28, Vo. 1, pp. 92-97. [4] JANG GYU LEE, CHAN GOOK PARK, HEUNG WON PARK,“Multiposition Alignment of Strapdown Inertial Navigation System”, IEEE Transaction on [5] JIANG CHENG FANG, DE JUN WAN, “A Fast Initial Alignment Method for Strapdown Inertial Navigation System on Stationary Base”, IEEE Transactions on Aerospace and Electronic Systems, 1996, Vo. 32, No. 4, pp. 1501-1505. [6] Sage A P, Husa G W, “Adaptive fi ltering with unknown prior statistics”, Proceedings of Joint Automatic Control Conference, 1969, pp. 760-769 [7] Zhang Changyun, “Approach to Adaptive Filtering Algorithm”, Acta Aeronautica et Astronautica Sinica, 1998, Vo. 19, No. 7, pp. 96-99. [8] WANG Yonggang, WANG Shunhong, “Improved Sage- Husa Filter and its Application in GPS/INS Fault Tolerant Integrated Navigation”, Journal of Chinese Inertial Technology, 2003, Vo. 11, No. 5, pp. 29-32. [9] ZHANG Hongwei, DONG Jinming, LV Dan, “Improved Sage-Husa Filter and Its Application in INS/ GPS”, Navigation, 2005, No. 3, pp. 107-111. |
||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||
|


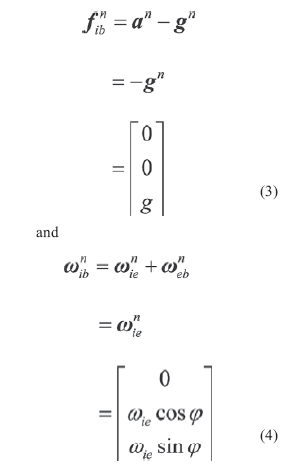

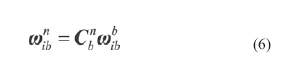
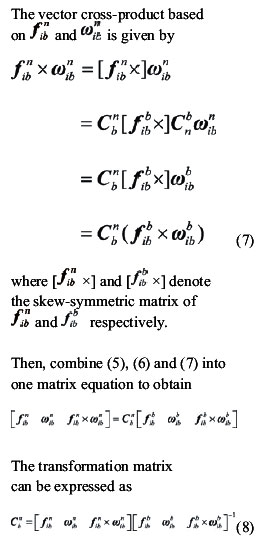
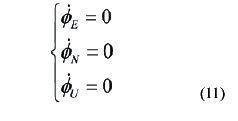


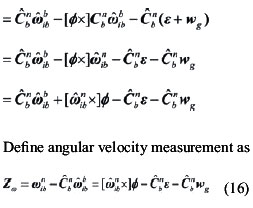
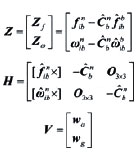















 (No Ratings Yet)
(No Ratings Yet)





