| Surveying | |
Vertical displacements of engineering structures
A case study of classification and prediction models during buildings reconstruction |
 |
|
The paper presents the results of research of various classification models for vertical displacements and their further prediction. When performing geodetic monitoring of complex engineering structures under reconstruction, the displacements of the structure is always unequally. In this case, it is impossible to construct a single prediction kinematic model for the whole structure.
Therefore, it is necessary to classify the displacements and divide the structure into blocks, within which displacements occur equally. After obtaining blocks within which the process of displacement can be considered uniform, the different prediction kinematic models of displacements by the method of random functions were investigated.

The basis of the presented research were results of geodetic monitoring of the façade structures of the historic building in Kiev (see Fig. 1 and Fig. 2). This historical building was built in 1930 in the architectural style which is known as “socialist realism”. The reason of these vertical displacements was the process of reconstruction, which was started in 2013 and was carrying out in difficult geological conditions. This reconstruction project has two important features. The first, during the reconstruction of the building, all structures were disassembled except for the façade one, which was kept by special metal retaining structures during reconstruction works (see Fig. 2).
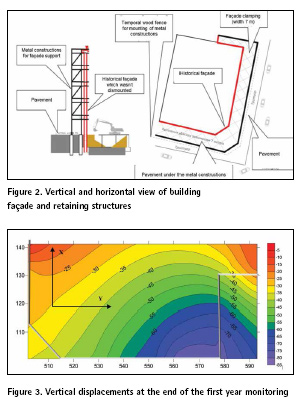
The second, with the height of the historical façade structure of 30 m, an underground parking of 20 m depth was built inside the building. The distance between the historical part of the façade that was kept by metal structures and the edge of the underground parking pit was only 5-6 m. Under such conditions, the vertical displacements in some places exceeded the allowable displacements by ten times and reached 110-120 mm for two years.
The results of geodetic monitoring in form of deformation surface are presented in Fig.3.
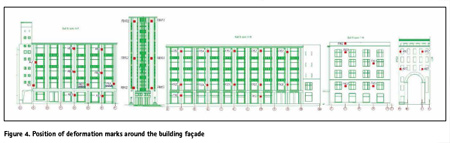
From Fig. 3 is clear that deformation process is not uniform. In Fig. 4 deformation marks that were installed around the building façade are presented.
Prediction by using random functions
At the study and prediction of structure vertical displacements, we should consider two tasks:
▪ determination of the nature and distribution of vertical displacements within the structure;
▪ construction of adequate prediction model.
The first task is logically connected with the second. Determination of the nature and distribution of vertical displacements within the structure makes it possible to allocate the deformation blocks within which the deformation process is described by the same laws (equations). Thanks to this, it becomes possible within the block with statistically identical displacements do not build a prediction model for each individual deformation mark and to use the entire volume of measurements to construct a prediction model that will describe the deformation process for any point within the block.
Deformation blocks determination
Let’s consider the first task of displacements modeling. Determination of the nature of change in displacements within the structure is a very difficult task. As a rule, the separation of the structure into blocks with statistically identical displacements is not obvious. The situation is further complicated by the presence of gaps in observations, or change the time of observation cycles that happens almost during monitoring process.
In work (Gulyaev, Yu.P. et al., 2013), authors presented their algorithm for allocation of homogeneous deformation blocks. As a criterion for the formation of statistically homogeneous blocks, the authors use the coefficient of variation VΔS . At the first step the vertical displacements are placed in decreasing order. It is assumed that the mean values within the blocks are significantly different from the overall mean value, root mean square error within the block is minimal and approximately within the blocks. The vertical displacements group is considered homogeneous if 0,25≤VΔS ≤0,33.
From our calculations the coefficient of variation equal 0.32 and therefore, the deformation process of whole façade is homogeneous. However, from Fig. 3 we can conclude opposite. Thus, despite the statistical validity, the proposed criterion for calculating the number of homogeneous deformation blocks does not always ensure adequate acceptable results. In addition, in this method there is some arbitrariness in choosing the coefficient of variation, which significantly reduces the accuracy of the approach.
We proposed to use an alternative method for calculating the number of deformation blocks. This method is based on the use of cluster analysis of vertical displacements.
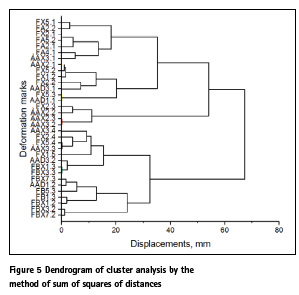
For the analysis, horizontal coordinates of the deformation marks and characteristics of soils at their locations were used. The following methods were investigated: sum of distances, maximum distance and sum of squares of distances. In Fig. 5 presents the results of a cluster analysis of vertical displacements by the method of sum of squares of distances.
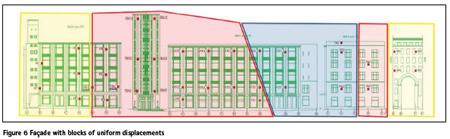
All the results of the cluster analysis, in contrast to the method of the coefficient of variation, showed the same distribution of all deformation marks on three blocks (Fig 6).
Within each block, the average value of the displacement is: red block – 75.4 mm; blue block – 44.0 mm; yellow block – 21.0 mm. Within each of these blocks, vertical displacements can be considered homogeneous.
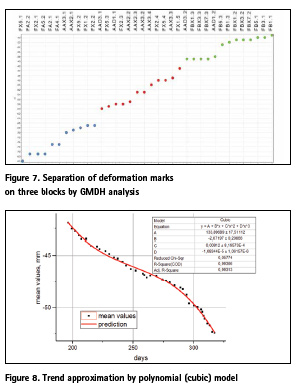
For control of the results of cluster analysis we used Group Method of Data Handling (GMDH). In Fig. 7 presents the results of GMDH analysis of vertical displacements which correspond to the results of the cluster analysis.
A necessary condition for the application of the theory of random functions is the normal distribution of the measured displacements in each block. Verification of displacements by the normal distribution was performed using the skewness and kurtosis criteria. Totally 113 cycles of observations were analyzed. By the results of this verification was determined that from 20th cycle all displacements have a normal distribution. We used for future prediction models construction 93 cycles. Below, we will present and study the prediction models for the first block (displacements in the range from – 82 mm to – 50 mm).
Prediction model construction
The whole process of prediction model construction can be divided in four steps.
Description of prediction model
The prediction kinematic model of the deformation process is constructed in the form of the following two functions (Gulyaev, Yu.P. et al., 2012): ;

The construction of prediction kinematic model is reduced to the

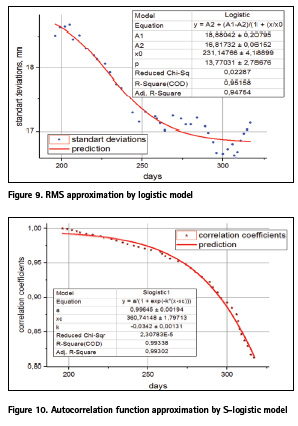
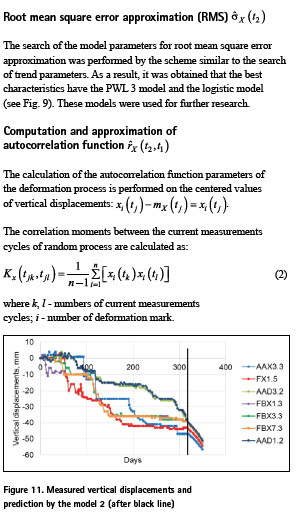
Using the results of measurements for the last 93 cycles, different models of trend prediction were investigated. The following types of models of different degrees were studied: polynomial (Kovačič, B. et al., 2009), power, exponential, piecewise linear, rational and logistic. Despite of the fact that many authors suggest using linear model, this type of model gave unsatisfactory results. For selection of the best model, the correlation coefficient, the accuracy of determining the model parameters, and the sum of the squares of the deviations were used. As a result, it was obtained that the best characteristics have piecewise linear model of three segments (PWL 3) and the third-degree (cubic) polynomial model (see Fig. 8). These models were used for further research.
Then, we turn to the normalized values:
![]()
From the normalized autocorrelation matrix, calculate the correlation coefficients. For approximation of autocorrelation function, we used the same models as previously. As a result, it was obtained that the best characteristics have the thirddegree (cubic) polynomial model and S-logistic model (see Fig. 10). These models were used for prediction models study.
Study of prediction models
According to our previous research were formed twelve different prediction models (see Tab. 1). All of these models were investigated using equations (1).
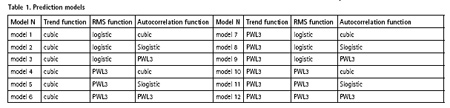
In order to define better model we made a prediction on ten cycles backward and compared prediction results with real displacements. By the deviations between predicted and measured values the root mean square error for each model was calculated. In such a way we got the better model, which has a minimum root mean square error and which consists from the next equations (see model 2 in Tab. 1):
These equations were used for the following forward prediction on ten cycles. One of the example of this prediction is presented in Fig.11.

Conclusion
Summarizing the studies made, we can confidently state that the possibilities of the theory of random functions in the prediction of deformation processes have not been fully investigated yet. The results above is showing that an obligatory condition for using the theory of random functions is the obtaining of homogeneous deformation blocks. In solving this problem is well-established cluster analysis method. However, to solve this problem, ANOVA method can also be used which needs further investigation.
As a result of the study of various prediction models, optimal prediction models for the trend, root mean square error and autocorrelation function were obtained. The results of this study confirm that for complex deformation processes, simple linear and exponential models are ineffective. Further, to improve the quality of prediction models, it is recommended to conduct in-depth statistical analysis of measured vertical displacements in order to avoid blunders and systematic errors.
References
[1] Kovačič, B.; Kamnik, R.; Kapović, Z. 2009. Mathematical Analysis of Measured Displacements with Emphasis on Polynomial Interpolation, In Geodetski list: ISSN 0016-710X. Vol.63 (86), No. 4 (2009), pp. 315-327.
[2] Gulyaev, Yu.P., Khoroshilov, V.S. 2012. Mathematical modeling. Analysis and prediction of deformations of structures based on geodetic data based on the kinematic model: lecture notes, Engineering Geodesy, SSGA, Novosibirsk, 93 p.
[3] Gulyaev, Yu.P., Khoroshilov, VS, Pavlovskaya, O.G. 2013. Mathematical modeling. Identification of hidden laws in the dynamics of landslide slopes in conditions of explosive influences and removal of large masses of soil according to geodetic data: lecture notes, Geodesy, SSGA, Novosibirsk, 131 p.












 (2 votes, average: 3.00 out of 5)
(2 votes, average: 3.00 out of 5)





Leave your response!