| Positioning | |
Single frequency GPS/Galileo precise point positioning
The results of the combined GPS/Galileo solution show a sub-decimeter level
|
 |
|
 |
|
GPS Precise Point Positioning (PPP) technique has attracted many users due to its lower cost and comparable precision to the differential technique. A drawback of a single GNSS system, however, is the availability of sufficient number of visible satellites in urban areas. With the launch of the new Galileo satellites, however, a PPP solution based on the combined GPS/Galileo measurements is feasible. Combining GPS and Galileo systems offers more visible satellites to users, which is expected to enhance the GDOP and the overall solution (Hofmann-Wellenhof et al., 2008).
In order to take full advantage of the new Galileo signals, it is essential that its stochastic characteristics are rigorously determined. In this research, sessions of Galileo measurements were used to study the stochastic characteristics of the new Galileo signal E1. As a byproduct, the stochastic characteristics of the legacy GPS signal P1 are also determined which were used to verify the developed stochastic model of Galileo signals. Combined L1/E1 signals of GPS and Galileo, respectively, were used to verify the stochastic model.
To verify the obtained results, the newly developed stochastic model is implemented to assess the effect of the stochastic characteristics on the combined GPS/Galileo PPP solution precision and convergence time.The results of the combined GPS/ Galileo solution show a sub-decimeter level of accuracy and an improvement up to 30% of the convergence time.
GPS/Galileo measurement errors
GNSS observations are affected by random and systematic errors, which must be considered to obtain accurate positioning. The accuracy of precise point positioning depends on the ability to mitigate all kinds of errors. These errors can be categorized into three classes, satellite related errors, signal propagation related errors, and receiver/antenna configuration errors (El-Rabbany, 2006).
GNSS errors attributed to the satellites, include satellite clock errors, orbital errors, satellite hardware delay, satellite antenna phase centre variation, and satellite initial phase bias. Errors attributed to signal propagation, include the delays of the GNSS signal as it passes through the ionospheric and tropospheric layers. Errors attributed to receiver/antenna configuration include the receiver clock errors, multipath error, receiver noise, receiver hardware delay, receiver initial phase bias, and receiver antenna phase center variations.
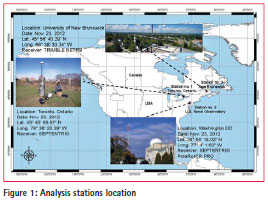
In addition to the above errors, combining GPS and Galileo observation in a PPP model introduce additional errors such as GPS to Galileo time offset (GGTO) due to the fact that each system uses a different time frame. GPS system uses the GPS time system which is referenced to coordinated universal time (UTC) as maintained by the US Naval Observatory (USNO). On the other hand, Galileo satellite system has its time frame namely The Galileo system Figure 1: Analysis stations location time (GST), which is a continuous atomic time scale with a nominal constant offset with respect to the international atomic time (TAI) (Hofmann- Wellenhof et al., 2008). Moreover, The GPS and Galileo measurements are on different reference frame, which should be considered in the combining PPP solution.
System noise test
The receiver measurement noise results from the limitations of the receiver’s electronics. Determining the noise level of the GNSS observations can be performed by testing the receivers. Two tests are normally used to determine the receiver noise level, namely the zero and short baselines tests. The zero baseline test uses one antenna followed by a signal splitter that feeds two or more GPS receivers. Several receiver problems can be investigated through zero baseline test, including interchannel biases and cycle slips. The use of a common antenna cancels out systematic errors such as multipath and the preamplifier’s noise. The short baseline test, on the other hand, uses two receivers a few meters apart on two consecutive days. In this case, the double difference residuals of one day would contain the system noise and the multipath effect. As the multipath effect repeats almost every day for a GPS system, differencing the double difference residuals of two consecutive days will cancel out the multipath effect and leave the system noise. However, multipath effect is not repeatable for the Galileo satellite system as the Galileo orbit parameters lead to a period of about 14 hours 4 min 45 sec and a ground track repeat cycle of about 10 days which is equivalent to 17 cycles (Hofmann-Wellenhof et al., 2008).
In this research, a short baseline test is used to determine stochastic characteristics of Galileo E1 signals. Usually, this test is performed using the same type of receivers. Unfortunately, two different receivers were available (Septentrio and Trimble) for the test, which can observe the Galileo measurements. This, however, were considered when processing the data. Differencing the pseudorange and carrier phase equations of each receiver cancels out the geometric term, satellite and receiver clock error, and tropospheric delays. The remaining terms include the satellite and receivers’ hardware delays, ionosphere error, the ambiguity parameter and the system noise.
The phase measurement noise has been neglected due to its small size compared to that of the pseudorange measurements (Elsobeiey and El-Rabbany, 2010). The receiver hardware delay is assumed to be stable over the observation period, almost four hours in this research, while the ambiguity parameter and initial phase bias are constants for a continuous session of measurements (Hofmann-Wellenhof et al., 2008). As such, they can be removed from the model by differencing with respect to the first value of the series.
Stochastic model development
The stochastic properties of the observations are reflected in the observations weight matrix which includes their absolute and relative accuracies with respect to each other. In the PPP modeling, most of the available observations stochastic models are empirical models such as the sine or cosine model, exponential and polynomial models. All of these stochastic models are function of the satellite elevation angles. These models may not be accurate enough for all receivers’ models and the new GNSS frequencies.
The differenced measurements shown in Equation 9 are divided into nine bins depending on the satellite elevation angle, starting from 0° to 90° with increments of 10° (i.e., 0º to 10º, 10º to 20º, etc.). The least square best-fit model that relates the standard deviation and satellite elevation angle is used to present the stochastic model.
Results and discussion
A combined PPP of GPS L1 with Galileo E1 solution is presented in this research. The GPSPace PPP software from Natural Resources Canada (NRCan) was modified to handle data from both GPS and Galileo systems, which enables a combined GPS/Galileo PPP solution. The NOAA ionospheric correction model was used to correct for the ionospheric delay (Smith, 2004). In addition, the NOAA model is used along the Vienna mapping function to correct the tropospheric delay (Ibrahim and El- Rabbany, 2008). International GNSS service (IGS) precise orbital and clock corrections are used for GPS satellites (Kouba, j. 2009). On the other hand, COoperative Network for GIOVE Observations (CONGO) network precise satellite orbital and clock corrections are used for Galileo satellites (Montenbruck at al., 2009).
The PPP analysis is done on two stages. The first stage studies the effect of combining the the measurements of GPS and Galileo satellite systems on the PPP solution in the urban areas with different cut-off angles. The second stage, on the other hand, compares the PPP results obtained from the existing empirical stochastic model, namely the sine model, and the newly developed stochastic model.
Combined GPS/ Galileo PPP results
To simulate a dense urban environment, different scenarios were considered in this research using cut-off elevation angles of 5, 15, 30, and 45 degrees. GPS and Galileo measurements of three stations located in Ontario, New Brunswick and Washington D.C, respectively, were used in the analysis. Figure 1 shows the locations and the receiver information of the three stations.
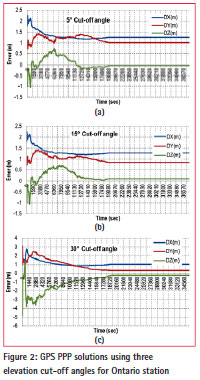
Due to space limitation the results of the Ontario station is presented for both GPS system only and the combined GPS/Galileo PPP solution at different elevation angles.
Figure 2 shows the results of the GPS PPP solutions using three cut-off angles, namely 5°, 15°, and 30°. The GPS PPP solution at 45° cut-off angle is not possible because there are no enough visible GPS satellites at this location.
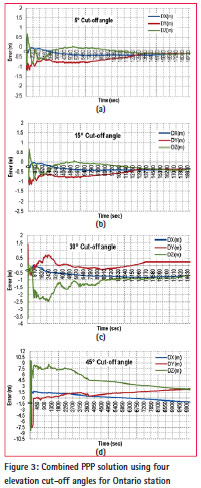
Figure 3 shows the results of the combined GPS/Galileo PPP solution at different cutoff angles, namely 5°, 15°, 30°and 45°. The Galileo satellite system can offer more satellites at 45° cut-off elevation angle for both the Ontario and Washington D.C. stations. With the additional Galileo satellites, it becomes possible to have a PPP solution at these two stations (Ontario and Washington D.C.) at 45° cut-off elevation angle. The results shown in Figure 3 show that a decimetre-level accuracy is possible with single-frequency GPS/Galileo PPP in the static mode, which is comparable to the GPS dual-frequency solution.
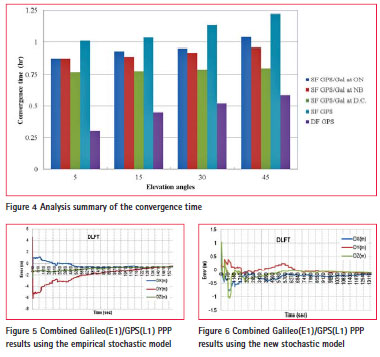
Figure 4 shows a summary of convergence times for single-frequency PPP solutions of both GPS and combined GPS/Galileo measurements at each of the three analysis stations. In addition, Figure 4 shows the convergence times at the same analysis stations for dual-frequency GPS solution, which are used to assess the GPS/Galileo combined PPP solution.
It was found that the PPP solution convergence time was improved by 20% to 30% with single-frequency GPS/Galileo when compared with single-frequency GPS solution.
Verification of stochastic model
To verify the determined stochastic characteristics of the Galileo E1 signal, Natural Resources Canada (NRCan) GPSPace PPP software was modified to handle the determined stochastic models. In order to verify the stochastic model, the GPS and Galileo measurements of four well distributed analysis station in North America and Europe are used in the PPP solution, namely DLFT, and GOP from Europe in addition to UNB, and USN from North America. Only the results of the DLFT station is presented in this paper as other stations have the same results. Figure 5 shows the results of the combined single frequency Galileo/ GPS of E1 and L1 signals using the empirical general sine stochastic model.
Figure 6 shows the results of the combined single frequency Galileo/ GPS of E1 and L1 signals using the new stochastic model. The results show that the new stochastic model improves the positioning accuracy and the convergence time, as well.
Conclusions
Single-frequency PPP algorithms were developed in this research to combine the E1 Galileo and L1 GPS signals. A short baseline test was performed to determine the stochastic characteristic of the E1 Galileo signal. It has been shown that Galileo satellite system can offer more satellites at 45° cut-off elevation angle to the GPS system, which makes the PPP solution possible at this high cut-off angle. The results showed that a sub-decimetre positioning accuracy and up to 30% improvement in the convergence time can be obtained with single-frequency GPS/Galileo PPP.
Acknowledgments
This research was partially supported by the Natural Sciences and Engineering Research Council (NSERC) of Canada and by the Ontario Government. The authors would like to thank the International GNSS service (IGS) network and the COoperative Network for GIOVE Observations (CONGO) for providing the satellites precise products.
References
El-Rabbany, A. (2006). Introduction to GPS: The Global Positioning System. Artech House Publishing.
Elsobeiey, M. and A. El-Rabbany (2010). “On stochastic modeling of the modernized global positioning system (GPS) L2C signal.” Journal of Measurement Science and Technology, Volume 21, Number 5, pp. 1-6.
Hofmann-Wellenhof, B., H. Lichtenegger, and E. Wasle (2008). “GNSS global navigation satellite systems; GPS, Glonass, Galileo & more”. Springer Wien New York. 501pp.
Ibrahim, H. E., and A. El-Rabbany (2008). Regional stochastic models for NOAAbased residual tropospheric delays. The Journal of Navigation. 61. 209-219.
Kouba, J. (2009). A guide to using international GNSS service (IGS) products. Available at http://igscb. jpl.nasa.gov/igscb/resource/pubs/ UsingIGSProductsVer21.pdf
Montenbruck, O., Hauschild, A., Hessels, U., Steigenberger, P., Hugentobler, U. (2009). CONGO first GPS/ Giove tracking network for science, research. GPS World, 20(9), 56-62. Smith, D. A. (2004). Computing unambiguous TEC and ionospheric delays using only carrier phase data from NOAA’s CORS network. Paper presented at the plans 2004. Position location and navigation symposium, 26- 29 April 2004, Piscataway, NJ, USA.












 (8 votes, average: 4.13 out of 5)
(8 votes, average: 4.13 out of 5)





Leave your response!