| Geodesy | |
Numerical simulations of the optimal geodetic conditions with radioastron
The feasibility for the estimation of EOPs has been investigated, then appropriate number of stations and epochs for the estimation of parameters have been analyzed |
|
 |
|
||||
 |
|
||||
 |
|
||||
 |
|
||||
Space Very Long Baseline Interferometry (SVLBI) is the unique space technology that can directly interconnect the three reference systems, which include the Conventional Inertial System (CIS) fixed in space and defined by radio sources, the Conventional Terrestrial System (CTS) fixed to the Earth and defined by a series of observing stations on the ground, and the dynamic reference system defined by the movement of a satellite. In this paper, the Space VLBI mathematical model with notation parameters, and its feasibility for estimation of EOPs are discussed. Simulations have been done for the SVLBI observations and related parameters for RADIOASTRON. With the results of the simulation, the feasibility for the estimation of EOPs has been investigated, then appropriate number of stations and epochs for the estimation of parameters have been analyzed.
Introduction
For all the three pillars of space geodesy (the geometry of the Earth surface and its displacements, the orientation of the Earth axis and its rotation speed, and the Earth’s gravity field and its time variations), well-defined, highly accurate and stable global Earth-fixed and celestial reference frames are of primary importance. Over the last decade considerable changes took place in space geodesy: the accuracy of the space geodetic techniques has improved dramatically up to
for geometric geodesy, Earth rotation and gravity field measurement. Many new missions are being prepared, planned, or on-going. All these developments pose new and demanding challenges concerning the consistency and accuracy of the three pillars and thus better-defined, more accurate and stable global Earth-fixed and celestial reference frames are crucial to meet these challenges. As a new and rapidly developing technique, SVLBI has tremendous potentials in geodetic research. SVLBI can not only directly interconnect the above two reference frames by determining the 5 Earth orientation parameters (EOPs) which
Following the VLBI Space Observatory Programme (VSOP) of Japan, another Space VLBI mission, called RADIOASTRON, is being planned by Russia with international collaboration for a launch as early as 2010. The two VLBI observatories in Urumqi and Shanghai of China may participate in the observations.
However，the present and foreseeable practical realizations of SVLBI are driven by astrophysical goals. Also, with VSOP observations, the geodetic test result by Frey et al. (2002) showed that it was difficult for VSOP to improve the precision of the determination of EOPs with the astrophysical observation conditions. So, it is necessary to determine the optimal observing conditions,so that RADIOASTRON can be used to improve the precision of the determination of EOPs.
In this paper, the modified SVLBI mathematical model with the EOPs is introduced. The possibility of the model for estimating EOPs has been theoretically studied by Erhu Wei (2008a), and the estimable parameter sequence has been extracted too. Based on these results, the SVLBI observations and the values of related parameters for RADIOASTRON are simulated in this paper. According to the simulated parameters, a matrix A of observation equation will be designed to discuss the validity of the modified model for estimating different EOPs. Finally, the effect of the number of stations, the number of observation epochs and the observation interval on the precision of the EOPs is studied, and the conclusions are presented.
Mathematical Model
Geometric Model
Figure 1 Geometric Figure of Ground-Space Baseline
Adam (1990) has derived the mathematical model of ground-space VLBI time delay observation, in which there are no nutation parameters that are used to connect the terrestrial coordinate system and the celestial coordinate system. In order to improve this model, Erhu Wei et al. (2008a) has derived a new SVLBI observation model, which contained the nutation parameters and can be expressed as Eq.（3）.
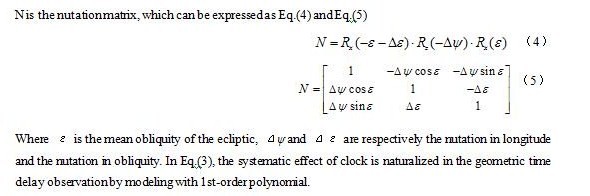
On the other hand, the coordinates of the ground station, satellite and radio source are transformed to the real celestial coordinate system at the moment 
by Eq.(3), which solves the transformation between the conventional celestial system and the real celestial coordinate system in the observation. So, all coordinates in the model are united in the same reference frame for the next derivation.
Estimable parameters
In the mathematical model, there are three coordinates of a station on the ground, three coordinates of the satellite, two coordinates of a radio source, three parameters of the Earth rotation, two nutation parameters, and the clock parameters. So the estimated parameters in the model can be listed in Eq.(6)
Model for Sensitivity Analysis
The adjustment is necessary for the time delay observation because the number of the SVLBI observations is very large. The least squares adjustment is adopted here, and the observation equation is derived from Eq.(3) and Eq.(7), which can be expressed as Eq.(8).
expressed as Eq.(11).
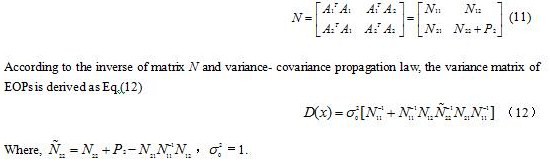
In this paper, only the sensitivity of EOPs will be investigated, and all the other parameters are assumed known or fixed. The precision of EOPs is studied by designing different matrix A.
Numerical Tests
Data for the Numerical Tests
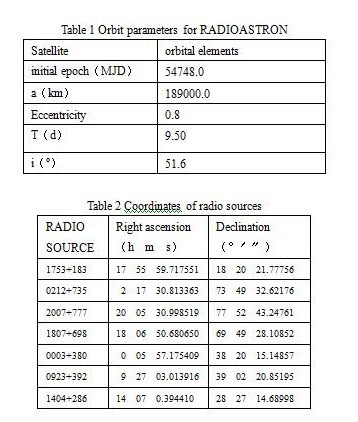
From the analysis above, only the value of matrix A needs to be calculated. So only the approximation of the parameters mentioned in Eq.(12) needs to be simulated. The coordinates of radio source, approximation of EOPs were found from the IERS Website in Oct.2008. And the Orbit parameters for RADIOASTRON were found from Website RADIASTRON in Oct.2008. With the prior value of these parameters, the partial derivative coefficient can be calculated and matrix A can be formed. In the simulation, some necessary parameters are listed in Table 1 and Table 2.
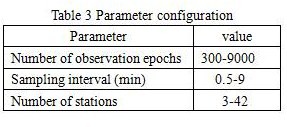
During the simulation, the number of radio sources is not changed. Each observation epoch contains only one radio source. In the experiment, 9 radio sources are used in order to improve the space distribution of the observation and enhance the visibility of the ground stations and the satellite antenna to the same radio source at the same epoch. The configuration range of other parameters is shown in Table 3.
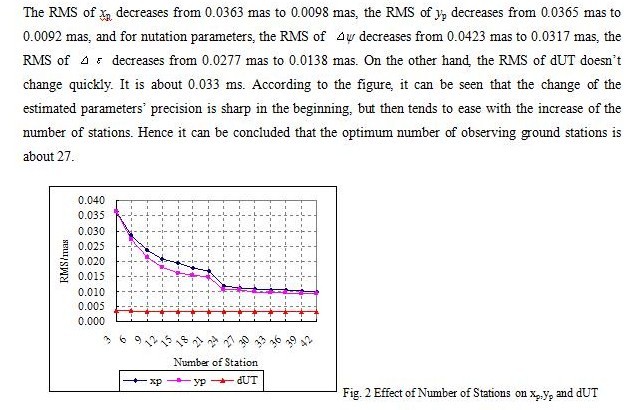
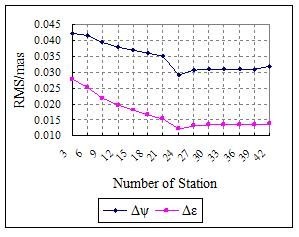
Effect of the Number of Stations
In order to analyze the effect of the increase of observing ground stations on the estimated EOPs, the number of observation epochs will be fixed as 10000, the observation interval will be fixed as 1 min and the number of stations will be increased from 3 to 42 by the step of 3. The results are shown in Fig. 2 and Fig. 3. It can be seen that the precision of each parameter is improved.
Fig. 3 Effect of Number of Stations on Nutation Parameters
Effect of Observation Epochs
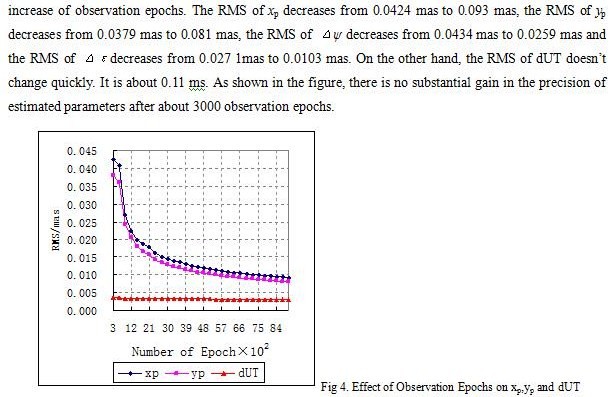
The results of the effect of the number of observation epochs on the estimated parameters are shown in Fig. 4 and Fig. 5. During the experiment, the number of stations is fixed as 24, the observation interval is fixed as 1 min, the number of radio sources is 9 and the observation epochs are increased from 300 to 9000. It is clear from the figure that the precision of the estimated parameters is improved with the
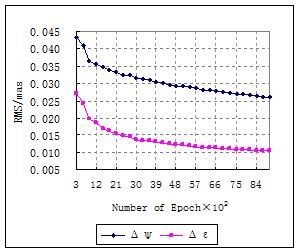
Fig 5. Effect of Observation Epochs on Nutation Parameters
Effect of Observat Interval
Discussions
According to the results above, it can be concluded that the optimum number of system parameters could be 27 observing stations, 3000 observation epochs and 1 min observation interval, which are propitious to improve the precision of EOPs estimated with the SVLBI observation from RADIOASTRON.
We must stress, however, that these are simulated results. In fact the present and foreseeable practical realizations of SVLBI are driven by astrophysical goals. The realistic observing setups for RADIOASTRON will be far from making possible to reach the optimum parameters as determined above. For example, the satellite will most likely observe together with a small network of ground radio telescopes (3-5 stations). Due to technical limitations, the pointing of the space-based radio antenna (i.e. the attitude of the massive satellite) cannot be changed quickly enough and over a large angle in the sky. However, the above simulation results will have great reference to the use of RADIOASTRON satellite for geodetic research.
Acknowledgements:
This research is funded by the national ‘863 Project’ of China (No. 2008AA12Z308), the National Natural Science Foundation of China (No. 40974003), the national ‘973 Project’ of China (No. 2006CB701301), and the project of education and research of Wuhan University (No. 20053039).
References
[1] Ádám J. (1990): Estimability of Geodetic Parameters from Space VLBI Observables, Ph. D. thesis, Ohio: The Ohio State University
[2] Kulkarni M.N. (1992): A Feasibility Study of Space VLBI for Geodesy & Geodynamics, Ph. D. thesis, Ohio: The Ohio State University
[3] Erhu Wei, Jingnan Liu, Wei Yan (2008a): On the Space VLBI Mathematical Model with Nutation Parameters[J]. The 5th IVS General Meeting Proceedings, 455–460.
[4] WEI Erhu, LIU Jingnan, et al. (2008b): On the Estimability of Geodetic Parameters with Space-ground and Space-space VLBI Observations. Proceedings of SPIE，2008.12:72851Q-1-9
[5]WEI Erhu (2006): Research on the Designment of Chinese Space VLBI System and Computation Simulation, Ph. D. thesis, Wuhan University
[6] Frey S., Meyer U., Fejes I., Paragi Z., Charlot P., Biancale R. (2002): Geodetic space VLBI: the first test observations. Advances in Space Research, Vol 30., 357-361
[7] Cui Xizhang, Tao Benzao (2001): General Surveying Adjustment[M]. Wuhan University Press (Wuhan)
[8] http://hpiers.obspm.fr/icrs-pc/
[9] http://www.asc.rssi.ru/radioastron/index.htm
My Coordinates |
EDITORIAL |
|
His Coordinates |
Paul Verhoef |
|
Mark your calendar |
NOVEMBER 2010 TO AUGUST 2011 |
|
News |
INDUSTRY | LBS | GPS | GIS | REMOTE SENSING | GALILEO UPDATE |
(No Ratings Yet)
Loading...
