| Mycoordinates | |
Malaysia precise positioning
|
||||||||||||||||||||||||||||||
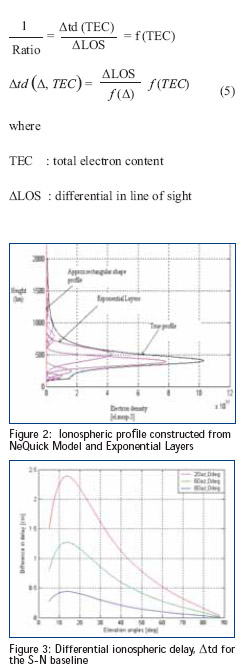
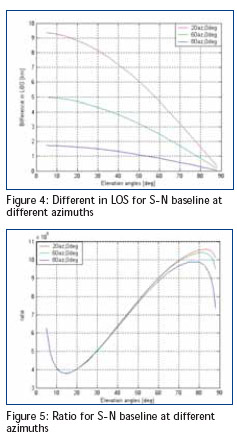
Global Positioning System (GPS) is currently one of the most popular global satellite positioning systems due to global availability of signal and performance. GPS employs two carrier frequencies which is L1 and L2 allowing receivers equipped with dual frequency operation to be used. Due to the inhomogeneity of the propagation medium in the ionosphere, the GPS signal does not travel along a perfectly straight line [1,2]. In addition, from Figure 1, the effects of the ionosphere can cause range-rate errors for GPS. 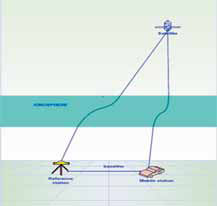 Figure 1: Exaggerated view of GPS signal in the ionosphere The Earth’s ionosphere plays a crucial role in GPS accuracy because this layer represents the largest source of positioning error for the users of the GPS after the turn-off of Selective Availability (SA). In order to provide ionospheric corrections for positioning and navigation for singlefrequency GPS receivers, the ionosphere needs to be mathematically described by a given ionospheric model. A good model Corrections and ionosphere modelsApplication of GPS for ionospheric sensing is now the subject of worldwide interest. In addition to this application, it has also been used widely in ionospheric study to model the electron content whilst the GPS signals propagate through the ionosphere. In this work, the ionosphereinduced errors in dGPS for short baseline are fi rst determined. After that the method of modelling and correcting these errors are provided. Very precise ray paths for both groups and phases were determined utilizing a modifi ed Jones 3-D ray tracing program, which includes the effect of the geomagnetic fi eld together with a Nelder– Mead algorithm to home in precisely on the satellite to earth station path [3]. Ionospheric error correction using modifi ed jones 3d ray-tracing Ionospheric profile using nequick model and exponential layer Ionospheric error correction on GPS signals due to the direction of mobile station base on reference station in DGPS Δtd=tdref-Δtdmob (1) LOS = LOSref -LOSm (2) Ratio = The ionospheric error for two closely separated stations can be evaluated and corrected. Calculations were performed for both reference and mobile stations located at equatorial region to investigatethe ionospheric effect for both the carrier phase and group paths for L1and L2. Since the ionospheric delay is a function of elevation angle, its variations are the main parameters to be considered in the modelling so the variation of azimuth and baseline direction will be investigated. The TEC and profi le shape also will be investigated because it also infl uenced by ionospheric error. Modelled the ratio using polynomial function Differential ionospheric delay model β : elevation angle at reference station
For accurate result, the carrier phase was primarily used instead of code pseudorange measurements. However, the integer ambiguity needs to be resolved. The infl uenced of the model can be examined by looking into its effect on the quality checking and on the carrier phase ambiguity resolution. Employing the ionospheric delay model and ambiguity resolution The integer ambiguity is the unknown integer number of whole cycles between satellite and receiver. The receiver can determine only the fractional part of the wavelength but not the integer, so the ambiguity resolution is essential for precise range determination [4]. In order to illustrate the contributions of the correction ionospheric model, a shorter time (less than one hour period from 03:00:00 to 03:59:45) for KTPK station and UPMS station which is 19.75 km was chosen to see how the correction infl uenced the ambiguity resolution where the observed satellites PRNs are 01, 03, 19 and 23 from both stations were selected. Float solution non integer ambiguity estimate is produced when the processing cannot resolve the ambiguity. On the other hand, when the processing can resolve the ambiguity to a correct integer number, it results in a fi xed solution. Table 1 illustrates that with these 4 satellites, (uncorrected data) the ambiguities were resolved with the occupation time of 03:39:00. By applying the correction model to PRN 23 and 19, ambiguities were resolved at 03:35:45, which is 00:03:55 earlier corresponding to uncorrected data and when the correction model was applied to PRN 23, PRN 19 & PRN 01, ambiguities were resolved at 03:31:00 which is 00:04:45 earlier corresponding to corrected data with PRN 23 and 19 only and 00:08:00 earlier compared to four satellites (uncorrected data).
ConclusionThe work presented here has shown promising results based on the utilisation of carrier phase observation for precise positioning. The model is mostly suitable for short baseline. Simultaneously the model could also be preferably used among the single frequency users. The results show an improvement in the correction of the differential ionospheric error over short baselines. By applying the ionospheric model the ambiguity resolution success rate is faster even when only correcting one satellite seen at low elevation angles. After the ambiguities are resolved, the variance ratio is larger and the reference variances are smaller. From the model we can get differential ionospheric delay in sub-centimetre accuracy. AcknowledgementsWe are grateful to Jabatan Ukur dan Pemetaan Malaysia (JUPEM) for providing the GPS data. The authors also would like to acknowledge Dr. H. J. Strangeways and Dr. R. T. Ioannides of Leeds University for permission to use a part of the ray-tracing program. References:[1] E. Sardon, A. Rius and N. Zarraoa, Estimation of the transmitter and receiver differential biases and the ionospheric total electron content from Global Positioning System observations, Radio Science29, 1994, pp. 577-586, |
||||||||||||||||||||||||||||||
|
Pages: 1 2

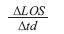 (3)
(3)














 (No Ratings Yet)
(No Ratings Yet)





