| Navigation | |
Integration in a receiver position computation
This paper covers the different technical aspects of the integration in a receiver position computation of the observable data from several navigation constellations. |
|
The reference scenario is defined by a set of navigation systems; each system is composed by a set of signal generators (constellation) and by a common time reference. Each transmitter must be synchronized to the time base; this operation is performed using different algorithms in order to generate a time correction to be transmitted to the receiver.
This correction is then applied to each observable measure in order to refer the data to the common time reference.
When the data are acquired by different sets of transmitters they have different time references (for example GPS time, Galileo time, Compass time etc.) and therefore in the position computation the receiver must take into account a further unknown variable for each constellation, i.e. the difference among the different time references.
In order to investigate the performance of the position computation when two constellations of transmitters are integrated, the performance parameters that characterize the geometric component of the error will be analyzed in simulated and real scenarios.
Brief introduction on the Diluition of Precision (DOP)
The DOP is a set of performance indexes that define a relation between the positioning performance and the geometric location of the transmitters.
For example the general expression that links the measurements error to the 4D user position accuracy is described by the GDOP (also called Geometric Diluition of Precision); the GDOP takes into account the three dimensional error plus the error in the computation of the receiver clock bias. As seen before considering the general problem of estimating the vector dX of 4 dimensions, given an observation vector ![]() , the minimum variance unbiased estimate of X is given by :
, the minimum variance unbiased estimate of X is given by :
For uncorrelated measurement noise ![]() and the estimate reduces to:
and the estimate reduces to: ![]()
Where P is the pseudoinverse of G.
We can obtain the GDOP expression from the computation of the covariance of the estimation x:
Given the previous expressions, in a more general way the DOP can be provided by the H matrix as follows:
The DOP matrix is directly linked to the covariance matrix of the optimal position estimator. The combination of the elements on the principal diagonal of the matrix H form the various DOP values. For example:
A geometric interpretation of the GDOP is that GDOP reduces when the determinant of G is increasing, or when the volume of the geometric figure composed by the satellite positions used for the position estimation is increasing (infact G depends on the Azimuth and Elevation of each satellite in view).
The problem of the two constellations
Suppose that the two constellations have different time reference, there is a bias between the measurements coming from different transmitters. The H matrix will have the following form:
From the matrix H we can define DOP in the same way as before but including a new term: TDOPG the relative to the second time offset.
There are two different strategies to take into account the fifth unknown:
• using an estimation of the offset and then transmitted by a service centre, for example the Galileo Time Offset (GGTO) broadcast by GALILEO
• computing the offset directly into the receiver
In the first case the performance of the integrated system are the same of a single system composed by a number of transmitters equal to the sum of the two constellations, provided that the time synchronization offset is estimated apart and transmitted to the receiver.
By this way the receiver can solve the position problem using a state vector of four unknowns. In the second case, if the estimation is made at receiver level, two cases must be distinguished:
• Only one transmitter is belonging to the second constellation
• More than one transmitter is belonging to the second constellation
If one considers only one transmitter of the second constellation, the corresponding measure contributes only to the offset determination and not to the position computation.
In fact in this case, in the following is shown the column of the P matrix related to the measurement of the only transmitter (the fourth unknown is the bias between the two constellation, while the fifth is the first constellation bias w.r.t. the system time).
So, independently to the number of transmitters of the first constellation, the measure obtained from the only transmitter of the second constellation will weight only the constellations bias solution, but not the position solution.
If we add more transmitters to the second constellation, from the P matrix it seems that all the measurements contribute to the position estimation.
It can be demonstrated that even if all the measurements are used to compute the position and the time offset, only above a certain number of transmitters used it is possible to have acceptable PDOP and TDOP values.
DOP computation with real measurement data
As a real scenario, measures of the GPS were integrated with the ones of another ranging source, simulating a configuration similar to the very first phase of the Galileo satellites deployment (In Orbit Validation phase – IOV).
During one of the integrations tests of the Galileo Test Range (GTR), located near Rome, we had the opportunity to collect measurement data from a constellation of four pseudolites and from the real GPS satellites.
So we had the opportunity to combine the measurement and define different integration scenarios like the simulated ones. We considered the following combinations:
• Only GPS satellites, as a reference scenario
• One GPS satellite and four pseudolites
• Three GPS satellites and four pseudolites
• Five GPS satellites and four pseudolites
• All the visible GPS satellites and four pseudolites.
The elevation of the pseudolites is very low while the GPS are chosen starting from those which had the higher elevation.
The configuration of the pseudolites is shown in the figure 1:
The red arrow represents the reference receiver and the white arrows correspond to the pseudolites locations.
For the mixed position estimation problem the fifth unknown must introduced as detailed in the following.
The definition of pseudorange in terms of time interval between the transmission and reception of a signal is the following:
Where ![]() is the time of transmission as reported by the satellite clock,
is the time of transmission as reported by the satellite clock,![]() is the real time of transmission with reference to the Constellation time base (i.e. GPS Time).
is the real time of transmission with reference to the Constellation time base (i.e. GPS Time).
![]() is the offset between the satellite clock and the reference time. For the receiver :
is the offset between the satellite clock and the reference time. For the receiver :
Where![]() is the time of reception as from the receiver clock,
is the time of reception as from the receiver clock, ![]() is the real time of reception with reference to the Constellation time base,
is the real time of reception with reference to the Constellation time base, ![]() is the offset between the receiver clock and the reference time. The real propagation time interval is:
is the offset between the receiver clock and the reference time. The real propagation time interval is:
The measured range is not c .t because of the time offsets, in fact:
t is also affected by propagation “errors” which are added to the ![]() (that corresponds to the line of sight between the antenna of the receiver and the one of the satellite):
(that corresponds to the line of sight between the antenna of the receiver and the one of the satellite):
![]() is due to the relativistic effects.
is due to the relativistic effects.
![]() is R/c, with R geometric distance between the satellite and the receiver:
is R/c, with R geometric distance between the satellite and the receiver:
The unknowns are four, x,y,z and ![]() .
.
The other elements are approximated by models in order to get the best estimation of the “errors”.
Considering a terrestrial transmitter like the one used in the simulations the equation that expresses the pseudorange is the same but with some remarks:
•![]() and
and ![]() are offsets with respect to the GTR time, that is different from the GPS time.
are offsets with respect to the GTR time, that is different from the GPS time.
Because ![]() and
and ![]() are zero (they are significant only in the space).
are zero (they are significant only in the space).
The pseudorange is now:
![]() like the GPS case is inserted in the navigation message of the pseudolite in the form of three parameters that allow the prediction of the correction in the future (8 minutes from the reception of the message).
like the GPS case is inserted in the navigation message of the pseudolite in the form of three parameters that allow the prediction of the correction in the future (8 minutes from the reception of the message).
When the two constellation are mixed, the system of equations must be modified in the following way.
The number of unknowns must be 5
• The receiver coordinates;
• DTRx the offset between the receiver clock and the GPS time;
• DTGTR-GPS, the offset between the GTR time and the GPS time.
When we want to simulate the GGTO term like in the case of the integration between GALILEO and GPS, we have to estimate one of the bias terms in an independent way.
The simplest method was to solve the estimation position problem using all the GPS satellites in view with good DOP value (without the pseudolites) and then taking the result as ![]() to be used in the mixed system (GPS + Pseudolites).
to be used in the mixed system (GPS + Pseudolites).
So a first run of simulations was carried on using an a priori estimation of the bias between the two time scales, i.e. reducing the problem to a 4 unknowns least square problem. In the second run the offset is solved by the receiver itself.
Simulation results
The simulations consider the PDOP and GDOP and the table below reports the number of transmitters (the first number is the Pseudolite constellation and the second the GPS one). A future version of the processing SW will also output the ![]()
“Autosync” stands for the computation of the offset between the two time scales, while “System sync” stands for the procedure to compute the bias of one of the two constellations before the integration of all transmitters.
It can be noticed that the PDOP and GDOP values decrease when increasing the number of transmitters of the second constellation. The values of the H matrix belonging to the second constellation are firstly used to solve the synchronization (i.e. to decrease the TDOP and ![]() terms) then, increasing the number of equations, they are used to get better performances of GDOP and PDOP.
terms) then, increasing the number of equations, they are used to get better performances of GDOP and PDOP.
When the bias is computed in an independent way, the performance are depending only on the number and geometric positions of the transmitters (all the equations contribute in the same way to all the DOP values).
So when observables from GPS and Galileo will be integrated at receiver level, it seems clear that the GGTO parameter contained into the Galileo navigation message will be a must. If obstructions (like urban canyons or indoor navigation) will avoid the reception of the navigation message, the GGTO will have to be sent through another communication channel (provided that the receiver is able to acquire enough satellites to get an acceptable DOP).
The same configurations have been used to compute the position of the receiver with the integrated constellation.
The first run, figure 2 has been carried on with only GPS satellites in order to establish the reference positioning performance (horizontal, towards east and north and vertical accuracy in a topocentric coordinates system).
Positioning error is limited in 4 meters around the reference position (obtained through RTK differential corrections sent by the Telespazio GNSS Differential Station).
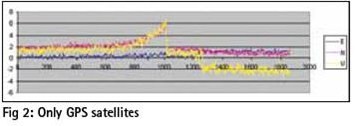
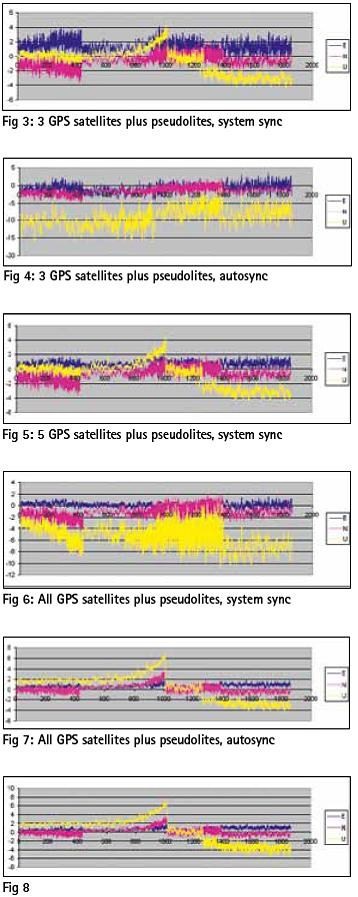
In the next runs, figures, 3 to 8, the comparison between the System sync and autosync scenarios is reported, in the configurations of 3, 5, all GPS satellites in view plus the pseudolites.
The performance improves with the increasing of GPS satellites in the same way as seen in the table of PDOP and GDOP.
In the last run, figure 7-8, the performance between the autosync and system sync scenarios is very similar, confirmed by the similarity between the DOP values.
Conclusions
The variance of the position error is comparable to the mean error, this is due to the noise in the receiver GPS bias estimation. Infact the bias is computed every second using Least Squares method as seen in the first paragraph; filtering the bias could give better performance to the position computation.
The DOP values depends on the positions of the transmitters with respect to the receiver location. As said before the DOP lowest value can be obtained in the middle of the constellation (in the middle of a tetraedric geometric form with the transmitters in the vertexes)
In the real configuration it was not possible to reach the optimal configuration (the GTR pseudolites are on the top of the surrounding hills and at different heights). The lowest value is found in the middle of the base of geometric figure formed by four pseudolites in the base and 7 satellites at the vertexes.
Finally the use of more constellations is useful only if the offsets are preliminary known. Moreover if one of the constellation is formed by pseudolites it is clear that their synchronization is very critical and that a modification is required in the firmware of currently available receivers to be used as an augmentation system because of the necessity to decode the particular navigation message.
References
GPS/GIOVE Interoperability: GGTO and Timing Biases Ricardo Piriz GMV, Patrizia Tavella INRIM, Jorg Hahn ESA ESTEC.
GNSS Time Offset Effect on GPSGalileo Interoperability Performance Inge Vanschoenbeek, Bernard Bonhoure, Marco Boschetti, Jerone Legenne CNES
Diluition of precision revisited Dessin Milbert Accounting for timing biases between GPS, Modernized GPS and Galileo Signals Chris Hegarty MITRE corporation, Ed Powers and Blair Fonville Time Service Department U.S. Naval Observatory
Understanding GPS, principles and applications Artech House 2nd edition, Kaplan, Elliot, Hegarty, Christopher, 2006
Global Positioning System: Theory and applications, Parkinson, Bradford, Spilker Jr., James 1996
 |
|
||||
 |
|
||||
My Coordinates |
EDITORIAL |
|
His Coordinates |
Sanjai Kohli |
|
News |
INDUSTRY | GPS | GALILEO UPDATE | LBS | GIS | REMOTE SENSING |
|
Mark your calendar |
AUGUST 2010 TO NOVEMBER 2011 |


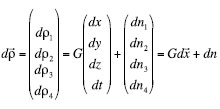

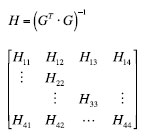
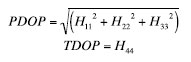
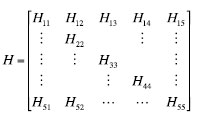



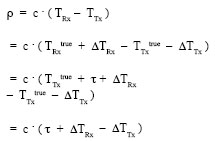
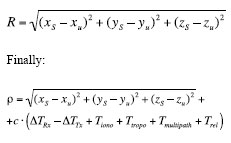












 (No Ratings Yet)
(No Ratings Yet)




Leave your response!