| Geodesy | |
Deformation analysis of the Balkan Peninsula from GPS data 2011-2016
The present work is an extended study of the surface movements of the territory of Bulgaria over the territory of the Balkan Peninsula (BP) and mainly of its central and southern part |
 |
|
 |
|
 |
|
The territory of the Balkan Peninsula is well known as a very active tectonic zone. Various geophysical, geological and geodetic methods and approaches have been applied to study and interpret the recent active earth crust movements [2], [6], [7], [9], [10] of the region. The present work is an extended geokinematics study not only for the territory of Bulgaria [13], [14] but it covers the territory of the Balkan Peninsula. Analysis and interpretation of the results obtained is based on the estimated station movements within the time span 2011-2016 from GNSS data processing and application of developed by the authors Finite Elements Method (FEM) for the space [13], [14]. The results of obtained relative deformations have been analyzed and mathematical-geometric interpretation has been performed. Suggested areas of extension (dilatation) and compression have been inferred.
Finite Elements Method (FEM) for the space
For the majority of studies the FEM is mainly used in the analysis of movements of stations, which are results from GNSS data processing in order to be obtained strain tensors and strain accumulation [1], [3], [5], [12]. Since the Balkan Peninsula is relatively large region, the method of finite elements is developed by the authors specifically for the space. More detail theory of the developed method has been presented in [13], [14]. Below only the key points of the theory are given.

The relative linear deformations m of the triangle sides are obtained from the following equations

Processing of GNSS observations
The territory of the study is covered by 33 GNSS permanent stations and 11 IGS GNSS permanent stations have been involved for referencing. On a tectonic map after Froizheim et al., 2014 [4], locations of the Balkan Peninsula GNSS stations are shown (Figure 1). Line AA’ is a line of cross section of the Hellenides and Rhodope Metamorphic Complex according to [4].
One week data from each year are used from all six years – 2011, 2012, 2013, 2014, 2015 and 2016. The data are processed with Bernese software, Version 5.0 in coordinate system ITRF2008. Obtained normal equations from data processing of each year have been combined in Addneq2 program of the Bernese software. Finally, the estimated station coordinates (X, Y, Z) and station velocity components (VX, VY, VZ) of all stations have been obtained by applying the least squares method with minimum constraint conditions for coordinates and velocities of 8 selected reference IGS stations in the system ITRF2008, referred to epoch 2005.0. The root mean squire (rms) errors of determined station velocities from data processing in north (VN) and in east (VE) components for all stations are 0,1-0,2mm/yr and for vertical component (VU) -0,2-0,3mm/yr. The estimated station velocity vectors in this study confirm their magnitude and directions obtained in previous investigations of the authors [13], [14], [15].
The relative movements of the stations with respect to the stable part of Europe (ETRF horizontal station velocity vectors in ETRF2000) have been derived from ETRF components of the Eurasia plate rotation pole [15] (Figure 2). The obtained horizontal station velocities vary from 0,3mm/yr up to 8,0mm/yr. For three stations (Brai, Alex, Nvrk) the obtained results are not reliable and they are not used in further analysis.
Analysis and discussion of deformations
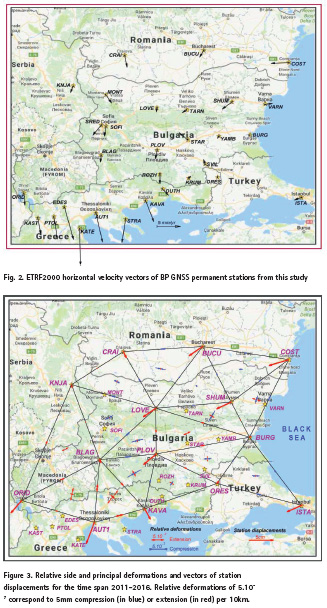
The final elements (triangles) have been configured approximately as equilateral triangles with approximately equal areas and not overlapping.
16 relatively uniform triangles (Figure 3) have been configured. The ETRF2000 coordinates (X, Y, Z) of all stations in each year have been transformed into ellipsoidal station coordinates (φ, λ, h) and then they have been transformed according to the equation (3) into Cartesian station coordinates (X0, Y0, Z0) onto the ellipsoidal surface used. The (X0, Y0, Z0) station coordinates have been used for determination of the ellipsoidal chords (baselines) between projected stations on the ellipsoidal surface by formula (4). The ellipsoidal chords form the triangle sides of every finite element in each year.
Three main types of deformations have been determined for the time period of five years 2011-2016 by FEM: station displacements, relative side deformations and relative principal deformations.
Station displacements
Displacements and their directions for each station within the time span 2011-2016 are shown with solid red lines in figure 3. The stations in central and eastern part of the region have moved to the south-west with about 3cm except stations Burg and Ores which movement is small, about 3mm. Stations in the west area – Crai, Knja, Blag, Kava have moved to the south-east as the displacement of the first three stations is 0,5-1,4cm and Kava has moved with 2,5cm. Two of the most southwest stations Orid and Aut1 have moved with 3cm and 5cm respectively to the south-west.
Relative side deformations
Relative deformations of compression (blue) or extension (red) of the triangle sides obtained by formula (5) are shown in figure 3. Small relative side deformations of compression (0,11.10-7-0,49.10-7, corresponding to 0,11-0,49mm per 10km) have been established for the triangles in the area of Moesia platform. Only the compression of sides Bucu-Crai and Cost-Burg is 1,8mm, respectively 1,6mm per 10 km. Deformations of compression have been also defined by finite elements (Knja, Love, Blag) and (Love, Blag, Plov), which cover the western part of the study region and by the finite element (Blag, Plov, Kava). The relative side deformations obtained are between 0,64.10-7 and 1,59.10-7. An area showing relatively compact deformation zone of extension has been inferred by the stations Knja, Blag, Aut1, Kava, Orid in the south-west part. The largest extensions in mentioned area belong to the sides Aut1-Kava (2,86.10-7), Blag-Aut1 (2,42.10-7) and Orid-Blag (1,46.10-7). The relative side deformations along the Black Sea cost and in the most south-eastern area (Burg, Ores, Ista) are also dominantly of compression. It should be noted that according to the developed FEM the type of side deformations (compression or extension) of each finite element depends on the directions of displacements of the respective triangle apexes (stations). The results obtained in this study for station displacements and side deformations of the finite elements (Figure 3) demonstrate a very good agreement.

Relative principle deformations
The relative principal deformations of each finite element are obtained by formula (9) and they are shown in figure 3 (compression in blue and extension in red).
Relative principal deformations of finite elements in the Moesia plate during the time period 2011-2016 are dominantly of compression from 0,35mm up to 2,03mm per 10km and directions are mainly northwest-southeast. The relative principal deformations of compression in direction northeast-southwest direction in the north-east area, close to the northern Black Sea coast are approximately the same size as those of their extension (northwest-southeast direction). The results for western part of the study region, closed between the stations Knja, Love, Plov, Kava and Blag and for the most south-east part show deformations of compression in directions southwest-northeast up to west-east and east-west. The extensions in the central-east part and in the central-south part of the region are approximately the same size as the compressions with north-south direction, respectively with southeast-northwest direction. Principal deformations of the most west and south-west part of the Balkans covering the north and northwest Greece, south Macedonia, part of Serbia and western Bulgaria are of extension in all direction. The relationship between directions of the principal deformations of each finite element and the directions of its side deformations is very close. Directions of the principal deformations of extension or compression of every finite element dominantly are defined by the type of deformations of the sides of the respective finite element. The obtained results for the principal deformations in this study confirm this relation (Figure 3).
Conclusion
The finite elements method in space is applied for deformation analysis mostly of the central and southern territory of the Balkan Peninsula for the first time and it is an attempt to be applied another approach in surface geokinematics. The suggested areas of extension and compression and their analysis present a mathematical-geometrical interpretation of the movements of the Balkans region. The results obtained in this study cannot be compared directly to the strain rates results of other studies of the Balkan Peninsula due to the different nature of the approaches.
Acknowledgements
We would like to thank the team of IPOS Ltd. for kindly provided us all necessary BULiPOS GNSS data for the processing.
References
[1] Bogusz, J., A. Klos, M. Figurski, M. Jarosinski, B. Kontny. (2013). Investigation of the reliability of local strain analysis by means of the triangle modelling. Acta Geodyn. Geomater., Vol. 10, No. 3 (171), 293–305.
[2] Burchfiel, B. C., R. W. King, A., Todosov, V., Kotzev, N., Dumurdzanov, T., Serafimovski, B., Nurce. (2006). GPS results for Macedonia and its importance for the tectonics of the Southern Balkan extensional regime, Tectonophysics, 413, 239–248.
[3] Deniz, I., H. Ozener. (2010). Estimation of strain accumulation of densification network in Northern Marmara Region, Turkey. Nat. Hazards Earth Syst. Sci., 10, 2135–2143, www.nat-hazards-earth-syst-sci.net/10/2135/2010
[4] Froitzheim, N., S. Jahn-Awe, D. Frei, A. N. Wainwright, R. Maas, N. Georgiev, T. J. Nagel, J. Pleuger. (2014). Age and composition of meta-ophiolite from the Rhodope Middle Allochthon (Satovcha, Bulgaria): A test for the maximum-allochthony hypothesis of the Hellenides, Tectonics, 32, doi:10. 1002/2014TC003526.
[5] Hu, Y., K. Wang, J. He, J. Klotz, G. Khazaradze. Three-dimensional viscoelastic finite element model for postseismic deformation of the great 1960 Chile earthquake. Journal of geophysical research, 2004, Vol. 109, B12403.
[6] Kotzev, V., R.W. King, B.C. Burchfiel, A. Todosov, B. Nurce, R. Nakov. (2000). Crustal motion and strain accumulation in the South Balkan Region Inferred from GPS Measurements, in Husebye, E., ed., Earthquake monitoring and seismic hazard mitigation in Balkan countries: Proceedings of the NATO Advanced Research Workshop on Earthquake Monitoring and Seismic Hazard Mitigation in Balkan Countries, Borovetz, Bulgaria, 11–18 September 2005: NATO Science Series IV: Earth and Environmental Sciences. Volume 81, 19–43.
[7] Matev, K. (2011). GPS constrains on current tectonics of southwest Bulgaria, northern Greece and Albania. Thesis, Doctor of university of Grenoble, 203 pp.
[8] Milev, G., Dabovski, C. (Eds). (2006). Geodynamics оf the Balkan Peninsula, Monograph, Reports on Geodesy, Warsaw University of Technology, Institute of Geodesy and Geodetic Astronomy, 647 pp.
[9] Reilinger, R., S. McClusky, D. Paradissis, S. Ergintav, Ph. Vernant. (2010). Geodetic constraints on the tectonic evolution of the Aegean region and strain accumulation along the Hellenic subduction zone. Tectonophysics, 488, 22–30.
[10] Stangl, G., Ph. Mitterschiffthaler. (2015). A GNSS-derived Velocity Field of the Southern Balkan Peninsula. Geophysical Research Abstracts, 2015, Vol. 17, EGU2015-8362, EGU General Assembly 2015.
[11] Valev, G. (1987). Projection of points onto the earth ellipsoid. Geodesy, Cartography and Land Management, 4, 6-11. (in bulg.)
[12] Valev, G., P. Kastreva. (2006). Stress strain analysis of the Balkan Peninsula. Balkan Peninsula monograph, Reports on Geodesy, Warsaw University of Technology, No 5(80), 597-605.
[13] Vassileva, K., G. Valev (2015). Application of Finite Elements Method in space for deformation analysis of the territory of Bulgaria, Proceedings of the 8-th Congress of the Balkan Geophysical Society, 4-8 October, Crete, Chania, Greece, 5p. art. N. 26716.
[14] Vassileva, K., G. Valev. (2015). Deformation analysis of the Territory of Bulgaria from GNSS observations. Coordinates, Vol. XI, Issue 12, 12-15.
[15] Vassileva, K., Atanasova, M. (2016). Earth movements on the territory of Bulgaria and northern Greece from GPS observations. Comptes rendus de l’Académie bulgare des Sciences, Volume 69, Issue 11, 1473-1478.
[16] http://epncb.oma.be/_productsservices/coord_trans/
[17] ftp://olggps.oeaw.ac.at/CEGRN15/solutions











 (No Ratings Yet)
(No Ratings Yet)






Leave your response!