| Surveying | |
Accuracy evaluation of DGPS
|
||||||||||||||||||||||||||||
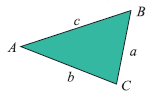
There are generally 2 types of users of DGPS for professional survey one is the National Mapping Agency and other large govt. organization who undertake Survey projects and the 2nd category is comprising of private survey set ups most of whom are first time users of DGPS and use DGPS to cut down on the time and efforts Involved in surveying with ETS (electronic total station) along with spirit levels. Conventional methodsNational Mapping Agency e.g. Survey of India have their established base lines established by them and in use for decades. Their procedure to evaluate accuracy of DGPS is simple in which they ask the venders to measure the base line vector and compare it against their established value and the agreement between the DGPS measured vector and their known value is an acceptable method of evaluation. Similarly other government organization adopts the same procedure as they are in a position to acquire the base line data. Which is not available to private surveyors as a matter of government policy? Private surveyors adopt a method where in they check repeatability of vector computed by DGPS or alternatively they measure a vector by ETS and compare the same with that obtained by DGPS. Both the methods applied by private surveyors are subjective and in cases of disagreement private surveyors, who have implicit faith on ETS do not ever consider that ETS measurement could have observational error. More over ETS need a clear line of sight and is therefore restricted to a vector limited to 4-5 km.To overcome their subjectivity, we at Pan India resort to a Geometric Solution independent of comparison method as well as to obviate the requirement of known control points, so diffi cult & cumbersome to obtain. Proposed methodThe principal utilized by us in simple term is solution called Trilateration. It is a well established geometric solution by which we can calculate internal angles of a closed fi gure such as Triangles & Rectangles When the vector length of sides is known. We have developed a small routine for this with due check by mollweids formula. Thus for evaluation purpose DGPS observation is made on the vertex of a triangle rectangle and vector length of sides is computed. With the vector lengths we compute the internal angles and sum up. For triangle the sum should add up to 180° any agreement with in ± one tenth of second is considered satisfactory and thus indicates that the vectors by DGPS have the requisite accuracy stipulated in the system brochure, which is ± 5mm + 1 ppm. For verifi cation we arbitrarily alter the length of any one side by more than 5mm + 1 ppm then recalculate the internal angles sum of internal angles does not come to 180° same procedure done by the competitors DGPS shows their quality and the customer can make objective judgment of the quality evaluation. This procedure when repeated with ETS will also show the accuracy achievable and procedural fl aws if any in measurements taken by ETS. After internal angles have been computed we also do a run down of azimuth and the closing error in Azimuth is shown to be less them one tenth of a second which is the stipulated accuracy of the DGPS being marketed by us. We have performed these tests with both single and dual frequency DGPS and have found to be stable for both single and dual frequency DGPS with in the distance limits stipulated for both (15 km for Single Frequency & 80 Km for dual frequency DGPS). Almost all of our customers have appreciated the logic of this evaluation scheme and many controversies of DGPS vis-à-vis ETS have been obviated. TrilaterationWhile most surveyors are aware of trilateration methods even so except for the National Survey Organizations other surveyors do not resort to trilateraties as routine. Therefore we feel that a little elementary explanation of trilateratior will be helpful in appreciating the import of the procedure explained above. In trilateration we get all three sides of triangle and an oblique triangle is any triangle that is not a right triangle. It could be an acute triangle (all threee angles of the triangle are less than right angles) or it could be an obtuse triangle (one of the three angles is greater than a right angle). Actually, for the purposes of trigonometry, the class of “oblique triangles” might just as well include right triangles, too. Then the study of oblique triangles is really the study of all triangles. Let’s agree to a convention for labelling the parts of oblique triangles generalizing the convention for right triangles. Let the angles be labelled A, B, and C, and let the sides opposite them be labelled a, b, and c, respectively. Solving oblique trianglesThe trigonometry of oblique triangles is not as simple of that of right triangles, but there are two theorems of geometry that give useful laws of trigonometry. These are called the “law of cosines” and the “law of sines.” There are other “laws” that used are but since the common use of calculators, these two laws are enough. The law of cosinesThis is a simply stated equation: c2 = a2 + b2 – 2ab cos C. It looks like the Pythagorean theorem except for the last term, and if C happens to be a right angle, that last term disappears (since the cosine of 90° is 0), so the law of cosines is actually a generalization of the Pythagorean theorem. Note that each triangle gives three equations for the law of cosines since we can permute the letters as we like. The other two versions are then a2 = b2 + c2 – 2bc cos A, and b2 = c2 + a2 – 2ca cos B. The law of cosines relates the three sides of the triangle to one of the angles. We can use it in a couple of ways. First, if we know one angle and the two adjacent sides, then we can determine the opposite side. For instance, if angle C = 60°, side a = 5, and side b = 8, then the law of cosines says c2 = 25 + 64 – 80 cos 60°. Since the cosine of 60° is 1/2, that equation simplifi es to c2 = 49, so c = 7. Second, if we know all three sides of a triangle, then we can use it to fi nd any angle. For instance, if the three sides are a = 5, b = 6, and c = 7, then the law of cosines says 49 = 25 + 36 – 60 cos C, so cos C = 12/60 = 0.2, and, with the use of a calculator, C = 1.3734 radians = 78.69°. Note: When triangle is obtuse, the cos C is negative. Suppose the three sides are a = 5, b = 6, and c = 10. Then the law of cosines says 100 = 25 + 36 – 60 cos C, so cos C = – 49/60 = – 0.81667. As we can see in the graphs above, the cosine of an obtuse angle is negative. This is fi ne, and our calculator will compute the arccosine properly. we’ll get C = 2.2556 radians = 129.237°. The law of sinesThe law of sines is also a simply stated equation
Note that the law of sines says that three ratios are equal. Like the law of cosines, we can use the law of sines in two ways. First, if you know two angles and the side opposite one of them, then we can determine the side opposite the other one of them. Second, if we know two sides and the angle opposite one of them, then we can almost determine the angle opposite the other one of them. Mollweide’s formulaIn trigonometry, Mollwedie’s formula, sometimes referred to in older texts as Molweide’s equations, named after Karl Mollwedie, this formula describes relationship between sides and angles in a triangle. Let a, b, and c be the lengths of the three sides of a triangle. Let ß, and ? be the measures of the angles opposite those three sides respectively. Mollwedie’s formula states that Each of these identities uses all six parts of the triangle – the three angles and the lengths of the three sides. Mollwedie’s formula can be used to check solutions of triangles. Evaluation of elevation specs.The known manufacturer of professional DGPS specify the elevation accuracy generally as double the horizontal accuracy specifi ed e.g. if an OEM specifi es horizontal accuracy as ±5mm + 1ppm, their elevation specs generally are ± 10mm + 2 ppm. All DGPS output elevation as ellipsoidal elevation and often the values are large and many times as (-) this causes ambiguity in appreciation of results. Most processing software that come with DGPS have an inbuilt programme for conversion of ellipsoidal elevation to optometric elevation using a geoid model EGM-96, which is not very reliable for India. Survey of India is developing a geoid model for India and even when it is ready its availability in public domain remains uncertain. Like assassin the horizontal specs, the elevation specs are best evaluated when precise elevator Benchmarks (BM) are available which at present are in a classifi ed category and not easily available. One of the other conventional practices of evaluation is repeatability. A number of points are considered and repeat observation of elevation is computed with DGPS data and mean and standard deviation is calculated to arrive at the accuracy obtained which should be in accordance of the accuracy specifi ed in the technical specifi cation of DGPS by the OEM. However it is our experience that usual customers are generally do not feel comfortable with such a laborious exercise and large volume of computational data which necessarily involves a meticulous study by the customers for which normal customers neither have time nor patience and many are not conversant with statistical methods used for the exercise. We at Pan India have therefore devised a simply and self evident procedure for evaluating the specifi ed elevation specs of the OEM mentioned in the technical brochure of the product. This procedure in brief is as given below: A base station in set up as suggested by the customer and an arbitrary elevation value of customers choice is assigned to the base station ground point a reccee of the area around base station is undertaken and a few points are selected for rover observation. These points are so selected that they should comprise of a pillar / parapet / distance stone so that the measurement is possible both at ground level as well as at top of such a stone / parapet etc. A series of observations are carried out with rover DGPS at the ground level as well as the top of such pillars / parapets etc. and the data is processed using the assigned elevation of base station and EGM-96. After the data is post processed. The difference in top and ground elevation of these points are tabulated. The actual difference of top and ground of these points is carefully measured using a standardized steel tape. The tape measured value is then compared with the DGPS computed value and max and mini variation is recorded. These this gives the customer a verifi able and physically evident value of the accuracy of elevation measurement by DGPS. The results so for have always been such that the maximum disagreement between the DGPS measurement and tape measurements has been well with in the accuracy specifi ed in technical brochure of the DGPS. The customer is always encouraged to get this exercise repeated with competitor DGPS and arrive at this own evaluation. Concluding remarksWe have utilized these procedures for extension of control for a large project of ONGC in fi eld of Geophysical exploration. However, instead of triangles we observed a network comprising rectangles one diagonal of each rectangle. |
||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||
|

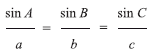
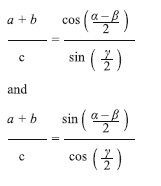













 (No Ratings Yet)
(No Ratings Yet)






My question is, do we need gps all the time? I was thinking, can’t the satellites in the orbit be replicated here on earth? A building is stationary. If the coordinates of a particular building is known, and it has a device that locates gps receivers in the area around it, and if there are 3 or 4 such buildings, knowing their coordinates and scanning gps receivers around their area, the distances from the gps receiver to each building can be calculated to find out the exact coordinate of the gps receiver.
Isn’t it all mathematics and calculations anyway?
Let’s assume, a mobile service provider like airtel or idea (or maybe all of them…) decide to install receivers or dgps in all their stations; after knowing their coordinates (each station i.e.), cant the location and coordinates of gps devices be found out?
I might be terribly wrong but I just wanted to share my thoughts and learn a bit…
Please email me if you want to at telepathicocean@gmail.com
Leave your response!