| Geodesy | |
The Gravimetric Quasigeoid Model UGQ2014 for Uganda
In this paper the Gravimetric Quasigeoid Model UGQ2014 for Uganda is computed using the KTH Method based on a combination of terrestrial and satellite gravity data |
 |
|
For many developing countries such as Uganda, the potential of GNSS has not been fully exploited due to the absence of accurate regional gravimetric quasi-geoid models. This means that the ellipsoidal heights, which are geometrical heights cannot easily be transformed into the physically meaningful normal heights which are required for most of the surveying/engineering applications. For many of these countries geoid determination is difficult due to the insufficient quantity and quality of terrestrial gravity data. However, new advances in geoid computation techniques coupled with the availability of gravity data from GRACE and GOCE satellite missions have made it possible to determine accurate regional geoid models based on a combination of terrestrial and satellite gravity data.
The gravimetric quasigeoid can be computed either directly by using the modified Stokes formula or indirectly by computing the gravimetric geoid first and then determining the quasigeoid-togeoid separation, which is then used to determine the quasigeoid. In this paper we use the later technique to the determine the quasigeoid over Uganda (UGQ2014) based on the Uganda Gravimetric Geoid Model 2014 (UGG2014) which was determined using the Least Squares Modification of Stokes formula with additive corrections (Ssengendo, et al., 2015a).
Principles of gravimetric geoid determination based on the KTH method
The Least Squares Modification of Stokes formula with additive corrections, commonly called the KTH method was developed at the Royal Institute of Technology (KTH) Division of Geodesy and has been presented in various studies and versions over the years; see e.g. Sjöberg, 2003a. For completeness only the basic formulas are presented in this paper. Compared to other methods, this method is superior because it is the only method that minimizes the expected global mean square error of the estimated geoid height. Hence, in contrast to most other methods of modifying Stokes’ formula, which only strive at reducing the truncation error, the KTH method matches the errors of truncation, gravity anomaly and the Global Geopotential Model (GGM) in a least squares sense based on the Least Squares Estimator for the geoid height, which is given by Sjöberg (2003b) as
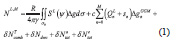

The combined topographic correction is computed as (Sjöberg 2001)

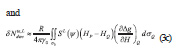
In the equations above, P and Q are the point on the Earth’s surface and the running point on the sphere, respectively,
![]()
disturbing potential for point P and y is the normal gravity at the normal height of point P and g is the Laplace harmonic in the sum in Eq. (3a) taken from a GGM, which requires the upper limit of the sum to be set equal to or below its maximum order.
Following Sjöberg and Nahavandchi (2000), the combined atmospheric correction can be computed as
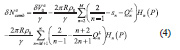

The ellipsoidal correction to order e2 of the modified Stokes formula is given by Sjöberg (2004) as
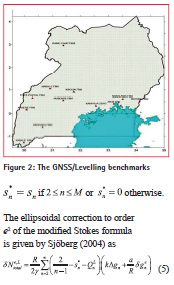
where is the Laplace harmonics of the ellipsoidal correction to the gravity anomaly, which can be decomposed into a series as shown by Sjöberg (2004), k = a/R–1 is a scale factor and a is the semi-major axis of the reference ellipsoid.
Geoid modelling database
The validation and evaluation of the several datasets required for geoid modelling is discussed in detail in Ssengendo, 2015. For completeness, we only highlight the data used in brief.
Gravity Anomaly Data
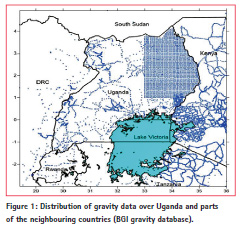
Terrestrial gravity data was downloaded from the BGI gravity database (http:// bgi.omp.obs-mip.fr/data-products/ Gravity-Databases/Land-Gravity-data). As shown in Figure 1, the data covers the area which lies between in latitude and in longitude. 7839 gravity points were obtained with 812 points identified as outliers and then removed from the gravity database. Using the Bouguer gravity anomaly the surface gravity anomalies were converted into reduced gravity anomalies, which are assumed to be smoother than the original surface gravity anomalies. This technique was used to overcome the challenge of interpolating unreduced gravity anomalies since the KTH method works on the full gravity anomaly without any reduction (Sjöberg, 2003b). Then the reduced gravity anomalies were interpolated to a denser grid and finally the effect of the topographic masses were removed from the Bouguer anomaly grid resulting in to free-air anomalies. The final grid at a resolution of was constructed using the method of Kriging with linear variograms.
Digital Elevation Model
The digital elevation model SRTM3 version 4.1 from the Consortium for Spatial Information of the Consultative Group of International Agricultural Research, Italy (http://www.cgiar-csi. org/data/srtm-90m-digital-elevationdatabase- v4-1) was used as it had the best quality in Uganda when compared to the ASTER DEM.
Global Geopotential Models
For the computation of UGG2014, we used the GOCE-only GGM GO_CONS_ GCF_2_TIM_R5 up to degree 280 since it had the lowest standard error of all GGMs evaluated with GNSS/Levelling data.
GNSS/Levelling
GNSS observations using Trimble R7 GNSS receivers were carried out carried out on 12 Fundamental Benchmarks (FBM) of the Uganda vertical network, whose normal-orthometric heights were readily available from the National Mapping Agency (see Figure 2). The ITRF08 coordinates of the 12 points were computed using the Bernese software version 5.2.
The Uganda Gravimetric Geoid Model 2014
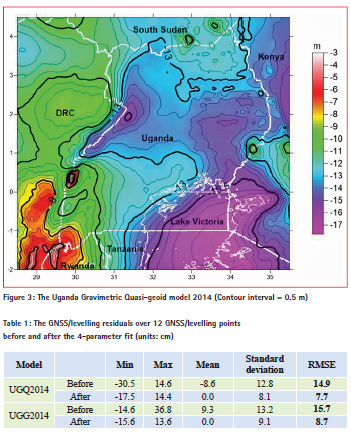
Based on Eq. (1), UGG2014 was computed using the datasets highlighted above. Its internal accuracy based on error propagation was estimated as 11.5 cm whereas the external accuracy based on comparison with the 12 GNSS/ Levelling points shown in Figure 2 was estimated as 15.7 cm and 8.7 cm before and after the 4-parameter fitting respectively (Ssengendo, 2015).
Determination UGQ2014 and its evaluation
The gravimetric quasigeoid model shown in Figure 3 was computed using Eq. (6) below
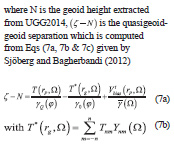


UGQ2014 was then independently evaluated using the 12 GNSS/levelling points shown in Figure 2. The results of the evaluation before and after 4-parameter fitting are reported in Table 1 along with the evaluation results for UGG2014.
Compared to UGG2014, UGQ2014 fits GNSS/levelling better by approximately 1 cm in terms of RMS both before and after the 4-parameter fitting. This is most likely a result of the fact that the quasigeoid is theoretically the proper zero reference surface for normal-orthometric heights, which are the heights used in Uganda.
Conclusions
The main purpose of this paper was to present the gravimetric quasigeoid model UGQ2014 for Uganda. The 14.9 cm and 7.7 cm Root Mean Square Errors (RMS) obtained by UGQ2014 before and after the 4-parameter fit respectively are very satisfactory given the quality and quantity of the terrestrial data used. If the standard errors for the ellipsoidal and normal-orthometric heights are 2.2 cm and 1.0 cm respectively, then the standard error of UGQ2014 can be estimated as 14.7 cm and 7.3 cm before and after the 4-parameter fit. We can see that the 4-parameter model has reduced the standard error of UGQ2014 by 7.2 cm or 48% by absorbing the systematic biases most likely arising from the current state of UVN.
For developing countries, the accuracy of UGQ2014 represents significant progress towards the goal of determining cm-level gravimetric geoid/quasigeoid models. First it highlights the robustness of the KTH Method in determining accurate regional geoid models based on a least squares combination of terrestrial and satellite gravity. Secondly and perhaps most important is the ability to determine cm-level accuracy even with insufficient quantity and quality of the terrestrial gravity data. Here the example of Uganda is instructive as with one gravity data point for every 65 km2, the approximately 7 cm accuracy of UGQ2014 is truly unprecedented. As part of future work, we anticipate that improvements in terrestrial gravity coverage as part of increased mineral exploration in the country will provide more gravity data that can be used to improve the accuracy of the gravimetric quasigeoid model. In addition more GNSS/levelling observations are needed so as to provide a much better homogeneous data set that can be used for validating and evaluating global and regional gravimetric quasigeoid models.
Acknowledgments
An earlier version of this paper was presented at the FIG Working Week in Sofia, Bulgaria, 2015. I am therefore gratefully to my co-authors for allowing me to use some of the results in that paper i.e. Ssengendo, et al., 2015b.
This study was funded by the Swedish International Development Agency (SIDA) and Makerere University, Uganda under the SIDA/SARECMakerere University Research Collaboration Program. We thank BGI for providing the terrestrial and WGM2012 gravity data.
References
CGIAR-CSI, 2014, SRTM ver4.1 data, online http://www.cgiar-csi.org/data/ srtm-90m-digital-elevation-database-v4-1 (accessed on 30th August, 2014)
International Gravimetric Bureau (BGI), 2013. Available from:
http://bgi.omp.obs-mip.fr/data-products/ Gravity-Databases/Land-Gravity-data, accessed in August/September, 2013. Ssengendo, R., 2015, A new height datum for Uganda based on a gravimetric quasi-geoid model and GNSS/ levelling. PhD Thesis, Royal Institute of Technology (KTH), Sweden
Ssengendo, R., Sjöberg L.E., Gidudu A., 2015a, The Uganda Gravimetric Geoid Model 2014 computed by the KTH Method, Journal of Geodetic Science, 5:35-46.
Ssengendo R., Sjoberg L.E., Gidudu A., 2015b, Computation of the Gravimetric Quasigeoid Model over Uganda Using the KTH Method, presented at the FIG Working Week 2015, May 17-21, Sofia, Bulgaria
Sjöberg, L.E., 2001, Topographic and atmospheric corrections of gravimetric geoid determination with special emphasis on the effects of harmonics of degrees zero and one, Journal of Geodesy, 75: 283-290.
Sjöberg, L. E., 2003a, A general model for modifying Stokes’ formula and its least squares solution, Journal of Geodesy, 77: 459-464
Sjöberg, L.E., 2003b, A computational scheme to model the geoid by the modified Stokes formula without gravity reductions, Journal of Geodesy, 77: 423-432
Sjöberg, L.E., 2004, A spherical harmonic representation of the ellipsoidal correction to the Modified Stokes formula, Journal of Geodesy, 78: 180-186 Sjöberg, L. E., 2007, The topographic bias by analytical continuation in physical geodesy, Journal of Geodesy, 81:345-350
Sjöberg, L. E., and Bagherbandi, M., 2012: Quasigeoid-to-geoid determination by EGM08.
Earth Sci. Inform., 5:87-91
Sjöberg, L. E., and Nahavandchi, H., 2000, The atmospheric geoid effects in Stokes’ formula,
Geophys J Int 140: 95-100











 (No Ratings Yet)
(No Ratings Yet)






Leave your response!