| Mapping - New | |
Suitability of projection for Defense Series Maps
It’s right time to close the discussion once for all and cement the choice of suitable projection for DSM |
 |
|
 |
|
 |
|
National mapping policy 2005 has recommended the usage of UTM as projection for Open Series Maps (OSM), however there were reservations on adopting UTM for Defense Series Maps (DSM). Accordingly LCC with certain proprietary modifications was found suitable for DSM. Probably, we would be the only country in the world with two projection systems being maintained at the national level. There were extensive arguments against this approach, forcing the map making agencies to contemplate on seeking UTM for DSM as well. There were however no valid technical reasons submitted at the apex to change the projection from LCC to UTM for DSM. Barring the administrative constraints in maintaining data in two projection systems at the national level, no other issues were found relevant in changing the projection for DSM to UTM. Varied views have been issued by number of experts in the Armed Forces towards selection of a particular projection, some purely administrative and some technical in nature. It is essential to study the effects in choosing two separate projections for OSM and DSM, besides the technical merits and demerits that such a policy would attribute to the systems and agencies involved in using data. The preparation of a report card on advantages and disadvantages, if any, in adopting any particular projection, from the perspective of Armed Forces, is quintessential. The nature of usage of maps in Armed Forces in view of the areas that are required to be mapped in the neighbourhood need a pragmatic approach in choosing a projection.
Introduction
It would not be exaggerating if it’s said that the Geospatial data utility literally grew from the way military leaders started demanding data. The military demand for usage of Geospatial data is not just in having the data, but in having accurate data. The continuous quest for accurate data grew over the years and no matter what kind of accuracy is feasible today, the scope for improvement still exists. Map reading skill is considered a basic skill for every military leader. National agencies are making incessant attempts in providing accurate data through paper maps since India’s independence. The everest maps were used in a number of battles with polyconic projection and LCC grid till date. The problems in maintaining such maps regionally, towards meeting global aspirations were taken note of and accordingly the datum has been earmarked for future mapping as WGS- 84. The debate on what would be the basic projection and what would be the suitable secondary grid for future Defense Series Maps (DSM) is on for over three years now. This paper attempts to bring out the perspective of Armed Forces and the necessity of using map data and the suitability of the projection, by bringing out the merits and demerits involved with each projection and the secondary grid.
Suitable Projection for DSM
Basic
A map projection is used to depict all or part of the spherical Earth on a flat surface. Without certain distortion, this is not feasible. Every projection has its own set of merits and demerits. There cannot be a “best” projection. The map making agency must select one best suited projection meeting their necessities, reducing distortion of the most important features. Map making agencies and researchers have devised almost boundless ways to project the image of the globe onto paper. The choice of projection depends upon the location of mapping, the Shape and Size of the region to be mapped and the theme or purpose of the map. If map is to be used for measuring areas, Equal area projection will suit, alternatively if the map is to be used for surveying and navigational purposes, as is the case for Armed Forces, the shape must be preserved at all costs, hence conformal/ orthomorphic projection would suit. A good projection is that which has an accurate scale factor close to unitary value in the entire region.
Methods of Choosing Projection
In trying to achieve this, there may be a necessity to select multiple projections over a large area. Multiple projections may not be permitted in all scenarios, specially for Armed Forces, hence projecting such a large area becomes really complex. This was partially followed regionally, by using polyconic projection with LCC grid, so far. Transverse Mercator projection is universally projected into multiple zones and projected independently. The nature of usage of maps dictates what kind of initiative is employed in choosing a projection. The north – south extent or east – west extent will certainly dictate the nature of projection. Incidentally, the extraneous and inherent parameters set for any operational needs established will dictate the projection.These are discussed below:
Extraneous Parameters:
[01] Existential Projection Type:- Planar, Cylindrical or Conical
[02] Focus of Projection:- Oblique, Normal or Transverse
[03] Placement of Projection:- Tangent or Secant
Inherent Parameters:-
[01] Preservation of Property:- Equi- Distant, Conformal or Orthomorphic and Equivalent or Equal area
[02] Generation:- Geometric, Semi Geometric or Mathematical

Existential Projection Type
India as a country is unique, where in both North – South and East – West extents are almost same, if the adjacent regions are not considered for mapping. The maps issued in everest datum have been from Turkey in the North to Yemen in the South as Western boundary and Gulf of Thailand in the South to Chinese eastern areas to the North as Eastern boundary. For mapping the Indian region, the general area extending in the east – west is approximately 90 degrees, which is much larger as compared to the North – South extent chosen for mapping. The suitability of a conical form of projection for the regions with the east – west extent is well known.
Focus of Projection
To cover the East – West extent of the Indian region accurately, the focus of a cone in the normal form will be adequate. In case the cylindrical form of projection is to be chosen, the normal or oblique coincidence does not suit, however the transverse coincidence can be customized to suit the region accurately. The cone will most suitably connect the adjunctions at the extremities; whereas the cylinder in the transverse position may have to be suitably adjusted to connect to adjunction. Accordingly, the choice of LCC stands out.
Placement of Projection
The East – West extent of the Indian region through conical nature can be mapped accurately with Secant positioning of the cone. The twin parallels to the standard parallel will augment the accuracy and reduce the distortion. The provision of having a unique central meridian passing through the centre of the cone will bring in mathematical simplicity. The cylindrical nature of projection with transverse coincidence, if adopted, the region will have to have separate central meridians based on the division of region into multiple zones. The mapping from the secant position will enable the ease of mapping.
Preservation of Property
Map or parts of a map can show one or more—but never all—of the following:
True Distances, True directions, True areas or True shapes. The basic orthomorphic maps maintain shapes and directions. On the Mercator projection a straight line drawn anywhere within its bounds shows a particular type of direction, but distances and areas are grossly distorted near the map’s Polar Regions.
Distances are true only along particular lines such as those radiating from a single point selected as the center of the projection on an equidistant map, whereas on every equal-area map, shapes are distorted. Sizes of areas are distorted on conformal/ orthomorphic maps, but the shapes of small areas are shown correctly. The degree and kinds of distortion vary with the projection used in making a map of a particular area. At higher latitudes on a small-scale Mercator map, the distortions are existent, though on a large-scale Transverse Mercator map of a small area in the same high latitudes, the distortion is almost non-existent.
Generation
The projection for Mercator is going to be semi-geometric whereas the generation of LCC will be a combination of geometric and mathematical. The mathematical linking of topology will be essential for maps of a small area or large area.
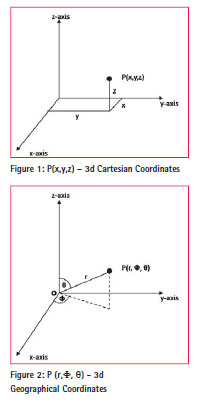
Mathematical Correlation between Cartesian Coordinates and Geographical Coordinates
The seamless conversion of 3-dimensional coordinates from Cartesian to Geographical and vice versa is simple and pure mathematics. The mathematical formulas along with the figures of 3d Cartesian and 3d polar coordinates given below can be used seamlessly for conversion from each other:-
The conversion equivalent parameters are:-
x = r sin θ cos Φ, y = r sin θ sin Φ, z = r cos θ, r = Sqrt (x2 + y2 + z2 ), cos θ = z/r
Mercator Projection
The point of discussion is to choose between UTM and LCC for DSM. The characteristics of Mercator projection and UTM will highlight the relevant issues concerning selection of projection for DSM. The basic Mercator projection, displayed at Figure 3, is primarily used for navigation or mapping equatorial regions. Any straight line on the map is a rhumb line, and the directions along a rhumb line are true between any two points on map, but a rhumb line is usually not the shortest distance between points. Distances are true only along the Equator, but are reasonably correct within 15° of Equator; special scales are to be used to measure distances along other parallels. Areas and shapes of large areas are distorted.
Distortion increases away from the Equator and is extreme in Polar Regions. A map, however, is conformal in those angles and shapes within any chosen small area. A map is not perspective, equal area, or equidistant, in which the equator and other parallels are straight lines, though spacing increases toward poles. The meridians, which are equally spaced straight lines, however meet the parallels at right angles.
Transverse Mercator
Lambert’s stroke of genius was to change the way the imaginary piece of paper touched the Earth. Instead of touching the Equator, he had it touching a line of Longitude (any chosen line of longitude). This touch point is called the Central Meridian of a map. This meant that accurate maps of places with northsouth orientated places could now be produced. The map making agency only needed to select a Central Meridian which ran through the middle of the map. The Transverse Mercator maps, which can be seen in Figure 4, are used for preparing quadrangle maps at scales from 1:24,000 to 1:250,000 for USGS. More quadrangle maps can be joined at the edges only if they fall in the same zone having the same central meridian. These are used generally for mapping large areas that are mainly north–south in extent. Distances are true only along the central meridian selected by the mapmaking agency or else along two lines parallel to it. But all distances, directions, shapes, and areas are reasonably accurate within 3° of the central meridian. The highlight here is that the distortion of distances, directions, and size of areas increase rapidly outside the 3° band. The accuracy of any Transverse Mercator projection quickly decreases from the central meridian. Graticule spacing increases away from the central meridian. The equator is straight and all other parallels are complex curves concaving near the pole. Central meridian and each meridian 90° from it are straight. Other meridians are complex curves concave toward central meridian. NATO recognised that the Mercator/ Transverse Mercator projection was highly accurate along its Standard Parallel/ Central Meridian and currently the prevalent projection has minimal distortion, as far as 5° away from the Standard Parallel/Central Meridian. Using this NATO designed a regular system for the Earth whereby it was divided into a series of 6° of longitudinal wide zones. There are a total of 60 longitudinal zones and these are numbered 1 to 60 – east from longitude 180°. A central meridian is placed in the middle of each longitudinal zone. The UTM system, hence, is not a single map projection. The problems are likely to occur in joining the individual zones and these are more prone while visualising larger areas in the East- West extent.
Lambert Conformal Conic
Presented by Lambert in 1772, projected mathematically on a cone, LCC projection is used primarily to map countries/ regions that are mainly east – west in extent. This is conceptually secant at two standard parallels. Despite extensive usage of UTM projection, LCC is still the most widely used map projection across the world. LCC retains conformality and the distances are true, the basic depiction of which is given in Figure 5. They are reasonably accurate elsewhere in adjacent regions. The distortion of shapes and areas are minimal at standard parallels, but increases away from them. Shapes on large-scale maps of small areas essentially are true. Map is conformal but is not perspective, equal area, or equidistant. By varying standard parallels in preparing map series, in various combinations in 7.5 and 15 minute size, the distortions can be drastically brought down. Map making agencies must suitably choose standard parallels keeping in view the North – South extent, to keep the distortion levels at higher latitudes within acceptable limits. LCC projection best suits large area mapping. For small area large scale mapping, the shapes and distances are maintained in LCC to the desired accuracy levels. Hence the aeronautical charts used by the Airforce, use LCC. The directions in LCC are true along long distances. This aspect influences the decision of choosing suitable projection for Armed forces in DSM.
Summary of Projection Properties
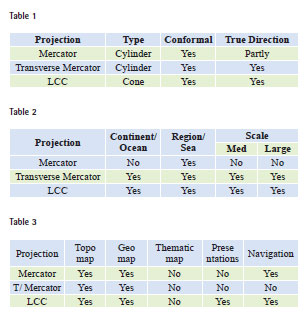
The summary of projection properties for the three projections discussed in the previous paragraphs in this paper can be summarized in the following tables, 1, 2 & 3. It is evident that all are conformal and maintain true directions and shapes. The tables are given below in the next page.
Effects of Projection to Armed Forces
Though OSM & DSM are likely to follow two projection systems, barring the administrative constraints, no operational reasons could be considered seriously impinging on the operational effectiveness or the interoperability at the apex level. Since the maps for hinterland and the trans-frontier areas would be issued in DSM, Armed forces will not face any situation of operating on two projections at any point in time. The inter service transfer of data; can continue to be undertaken in Geo-coordinate form, which can seamlessly be distinguished in respective systems in any projection of the user’s choice. It can be highlighted that the East – West extent to be covered in mapping has direct influence over the way the mapping needs to be organized. The conical nature with secant position will suit the projection type for East – West extent. The kind of projection to be used for DSM actually is influenced by the way maps are used. Military commanders will use paper maps in innumerous situations. Map reading is an inherent art possessed by military leaders. Survey and navigation in an unknown territory will be undertaken studying the paper maps. In such a scenario, having shapes and directions maintained, besides extending topology over zones and maps, is a mandatory necessity.
Conclusion
It’s right time to close the discussion once for all and cement the choice of suitable projection for DSM. National Mapping Policy 2005 has recommended rightfully the usage of UTM as projection for Open Series Maps (OSM), and LCC for Defence Series Maps (DSM). There are valid technical reasons why LCC suits DSM when compared to UTM. The projection however, can be interchanged in to each other without losing the accuracy or value. Hence, the discussion of proceeding ahead with any projection will only affect the way maps are printed, but will have no impact on the way the networked systems operate under tactical command, control, communication and intelligence environment. The systems at national level exchange Geospatial information in Geographical form, which can thereafter be displayed in the desired form of projection.
References
[01] Feeman, T. G . : Portraits of the Earth: A Mathematician Looks at Maps . American Matematical Society, Providence (2002)
[02] The Mathematics of GIS by Wolfgang Kainz, Dept of Geography and Regional Research, University of Vienna, Aug 2010.
[03] Banerjee, S . : R ev is iting S phericalTrigonometry with Orthoginal Projectors , College Math. J .35 (5), 375–381 (2004).
[04] Geogrpahic information systems and science by Paul A Longley, Michael F Goodchild, avid J Maguire and David W Rhind (John Wiley and sons Ltd) , Sep 2000.
[05] Chapter 10 of Coordinate systems and map projections for GIS (Mailing D) Longley PA, Goodchild, David J Maguire and David W Rhind.
[06] Flattening the Earth: Two housand years of map projections, Chicago University press by Snyder JP 1997.
[07] Scale in Remote Sensing and GIS, by Quattrochi DA and Goodchild MF 1996, Lewis Publishers.
[08] Elements of Spatial Data Quality by Kainz W, 1995 SC Guptill and JL Morrison.
[09] Bosowski, E . F., Feeman T. G.: The use of scale factors in mapanalysis: anelementary approach. Cartographica 34(4), 35–44(1997).
[10] Wikipedia Trilateration. http:// en. wikipedia. org.













 (3 votes, average: 2.67 out of 5)
(3 votes, average: 2.67 out of 5)





Leave your response!