| GNSS - New | |
Search for the plate transition zone in Bulgaria with GPS
The main objectives of this study are the estimation of Euler rotation vector
|
 |
|
 |
|
The region of Balkan Peninsula and in particular, the territory of Bulgaria characterizes with active tectonics and seismotectonics. A number of geological, geophysical and geodetic investigations demonstrate the recent activity of the region, and have tried to give a reasonable and adequate interpretation of the obtained results [2], [4], [6], [8], [11], based on the analysis of estimated stations velocities from GPS data processing.
This work is an attempt to contribute to clarify the boundaries of the Eurasian plate in the country by applying another approach for boundary determination, i.e., by applying the theory of Euler rotation pole to the estimated coordinates and velocities of freely accessible GNSS permanent stations operating in Bulgaria and nearby areas.
GPS data processing
For purposes of the study, data from 26 GNSS permanent stations have been used as 19 of them are in the territory of Bulgaria, 2 permanent stations in Romania, 4 permanent stations in northern Greece and 1 permanent station in north-east Turkey (Figure 1).
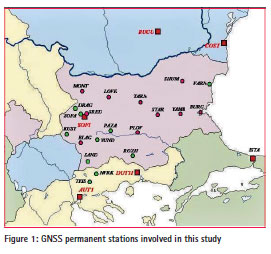
Velocity vectors used in this study were obtained earlier in two time frames [12], [13]. Station velocity vectors were estimated in [12], for the investigation of geodynamics of the territory of the Balkan Peninsula. For their estimation, one week of GPS data of every year from 2006 to 2010 were processed with the Bernese software, version 5.0 in ITRF2005. Part of the results obtained from these stations are used for this study, i.e., DRAG, SOFA, KUST, PAZA, YUND, SAND, VARN, ROZH, and SOfi. The other part of the stations was involved in a later investigation [13] of GNSS BULiPOS permanent network [9]. One week of GPS data of BULiPOS stations were processed with the same software, in the same coordinate system, every year from 2009 to 2011. To be consistent and comparable station velocity results in both works, all GPS data of BULiPOS network are reprocessed with the same IGS stations for datum definition as they are used in Vassileva, 2013a. New estimations of station coordinates and station velocity components (VX, VY, VZ) are obtained from their combined solutions in ITRF2005, referred to epoch 2000.0. For the local movements of the stations, which are more important for their behavior, the ETRF horizontal station velocity vectors (Figure 2) have been obtained by applying ETRF components of the Eurasia plate rotation pole [1] to the obtained ITRF2005 velocity vectors. Then they have been transformed into ETRF2000.
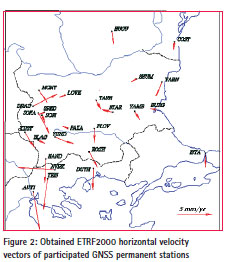
The magnitude of the obtained horizontal station velocities varies from 0,2mm/ yr up to 3,8mm/yr for the Bulgarian stations, and up to 10mm/yr for stations in northern Greece. Such small magnitudes of movements of points over the territory of the country have been also obtained by other researchers [2], [3], [5].
Estimation of the parameters of the Euler rotation pole The main objective of this item is the computation of different Euler rotation vectors and Euler poles, which give information about the motion of the respective plate. Each tectonic plate included in some kinematic plate model (absolute or relative) has altogether six parameters: Euler rotation vector Ω (ΩX, ΩY, ΩZ) and Euler pole (φ, λ, Ω). The relation between estimated parameters of a single station – Cartesian geocentric coordinates (X, Y, Z) and station velocity components (VX, VY, VZ), and unknown values of the Euler rotation vector – Ω (ΩX, ΩY, ΩZ) gives the linearized observation equation for the station. Using the estimated coordinates and velocities of GPS stations, it is possible to estimate the plate kinematic model by applying the least squares method. GPS velocities in a Cartesian geocentric frame can be modelled as [10]:

where P (X, Y, Z) is the vector defining the position of the GPS station, V (VX, VY, VZ) is the velocity vector at that station, and Ω (ΩX, ΩY, ΩZ) is the rotation vector defining the motion of the plate carrying the station.
Estimating Euler rotation vector Ω (ΩX, ΩY, ΩZ) , it is possible to calculate the Euler pole (φ, λ, Ω).
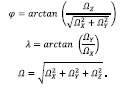
Nine sets of stations with their estimated ITRF2005 coordinates and velocities have been configured considering the tectonic setting of the territory of the country and respective parameters of the Euler rotation pole have been estimated.
Burchfiel et al., 2006 and Kotzev et al., 2008 suggest that the northern boundary of the Aegean extensional region passes through Central Bulgaria. Other researchers [3], [4], [7] also suggest that the boundary of the Eurasian plate follows the Balkan mountain chain. By this reason, two main sets are configured from all stations in northern Bulgaria and two stations in Romania (NB2), and respectively from all stations in southern Bulgaria, northern Greece and northern Turkey (SB2). The other sets are configured in such a way that stations from southern Bulgaria gradually are added to the northern set NB2, in order to be followed the changes of the estimated Euler parameters. The obtained results for Euler pole (φ, λ, Ω) of all sets are given in Table 1.

From all nine sets the closest result of the Euler rotation pole parameters to the estimated and officially accepted EUREF parameters (plate EUREF in Table 1) is the NB2 set, which consists of stations only in northern Bulgaria and two stations in Romania and SB2 set, which consists of stations only in southern Bulgaria, northern Greece and northern Turkey. Considering the results from other researches [2], [3], [4], [6], it is not quite understandable that the estimations of SB2 set show the belonging to the Eurasia plate as this territory is characterized with extensional processes. Differences of Euler rotation pole estimations between the other sets of stations and EUREF Euler rotation pole estimations varies between 10 o- 15o in latitude φ and between 6 o- 13o in longitude λ (Figure 3). These sets are combinations of stations from northern and southern Bulgaria.
Discussion
The results obtained in this study indicate that the majority of added stations to the northern territory of Bulgaria do not belong to the Eurasia plate. But for a few of the southern stations (set NSB7), it could be assumed that they also belong to the Eurasia plate. Therefore, the results obviously do not show quite a clear distinction between the transition zones, which is also an assumption of other studies (Stangl, 2011). Otherwise, all sets agree well in estimated angular velocity of the Euler pole Ω. From the analysis of the obtained parameters of the Euler rotation poles, it can be assumed that the North Bulgarian territory, northern from the Balkan Mountain chain and probably a small part of the central-eastern Bulgaria belong to the Eurasia plate.

Conclusion
The estimated parameters of Euler pole of the study territory on the basis of GPS processed measurements confirm the suggestion that the northern Bulgaria belongs to the Eurasia plate, but still its boundary, e.g., the transition zone cannot be clearly defined. Denser network of GNSS stations spread over the territory of the country could contribute to the clarification of the transition zone.
Acknowledgements
We would like to thank the team of IPOS company for kindly delivering of all necessary GNSS BULiPOS data for processing.
References
[1] Boucher, C., Z. Altamimi. Memo (2008): Specifications for reference frame fixing in the analysis of a EUREF GPS campaign. 2011,Version 8: 18-05-2011.
[2] Burchfiel, B. C., R. W. King, A., Todosov, V., Kotzev, N., Durmurdzanov, T., Serafimovski, B., Nurce. GPS results for Macedonia and its importance for the tectonics of the Southern Balkan extensional regime, Tectonophysics, 2006, 413, 239–248.
[3] Georgiev, I., D.,Dimitrov, P., Briole, E., Botev.Velocity field in Bulgaria and northern Greece from GPS campaigns spanning 1993-2008. Proceedings of 2nd INQUA-IGCP-567 International Workshop on Active Tectonics, Earthquake Geology, Archaeology and Engineering, Corinth, Greece, 2011, 54-56.
[4] Georgiev, I., D.,Dimitrov, E., Botev. Crustal Motion Monitoring in Bulgaria and Surrounding Regions by Permanent GPS Array. Proceedings of 7th Congress of Balkan Geophysical Society – Tirana, Albania, 7-10 October 2013, 5 pp.
[5] Kotzev, V., R. Nakov, Tz. Georgiev, B.C. Burchfiel, R.W. King. Crustal motion and strain accumulation in western Bulgaria, Tectonophysics, 2006, 413, 127–145.
[6] Kotzev, V., R.W. King, B.C. Burchfiel, A. Todosov, B. Nurce, R. Nakov. Crustal motion and strain accumulation in the South Balkan Region Inferred from GPS Measurements, in Husebye, E., ed., Earthquake monitoring and seismic hazard mitigation in Balkan countries: Proceedings of the NATO Advanced Research Workshop on Earthquake Monitoring and Seismic Hazard Mitigation in Balkan Countries, Borovetz, Bulgaria, 11–18 September 2005: NATO Science Series IV: Earth and Environmental Sciences. 2008, Volume 81, p. 19–43.
[7] Matev K. GPS constrains on current tectonics of southwest Bulgaria, northern Greece and Albania. Thesis, Doctor of university of Grenoble, 2011, 203pp.
[8] Milev, G., Dabovski, C. (Eds). Geodynamics оf the Balkan Peninsula, Monograph, Reports on Geodesy, Warsaw University of Technology, Institute of Geodesy and Geodetic Astronomy, 2006, 647 pp.
[9] Milev, G., K. Vassileva, I. Milev. Development and applications of DGNSS in Bulgaria. Proceedings of the International symposium on GNSS, Space-Based and Ground- Based Augmentation Systems and Applications, 2009, 73-77.
[10] Perez, J. A. S., J. F. G. Monico, J. C. Chaves. Velocity Field Estimation Using GPS Precise Point Positioning: The South American Plate Case. Journal of Global Positioning Systems, 2003, Vol. 2, No. 2: 90-99.
[11] Stangl, G. Velocity Fields from Geodesy to Geodynamics. Presentation at the Seminar, University of Vienna, 2011-04-12.
[12] Vassileva, K. Geodynamical study of the territory of the Balkan Peninsula from GPS solutions. Coordinates, June, 2013, 37-41.
[13] Vassileva, K. Effect of Datum Definition on Estimated Station Velocities from GPS Solutions: Case study. Proceedings of 7th Congress of Balkan Geophysical Society – Tirana, Albania, 7-10 October 2013, 5 pp.












 (1 votes, average: 2.00 out of 5)
(1 votes, average: 2.00 out of 5)





Leave your response!