| Positioning | |
Robotic forest harvesting process using GNSS satellite positioning data
In this paper we contribute experimental findings to the issue of the accuracy of GNSS location measurements in forest environments, by addressing the effects of harvester trajectory errors due to GNSS measurements |
 |
|
 |
|
 |
|
 |
|
 |
|
1 Introduction
Navigation often relies on high accuracy and high-update rate global navigation satellite systems (GNSS) such as GPS, Galileo, Glonass, Beidu, Navstar [1], however their deployment in the context of agriculture, vineyards, farming is far more frequent than in forestry. These fields are not behind in the adoption of robots, “precision farming”, and the use of drones [2]. In “precision farming”, mapping information is matched with GNSS measurements and vision/ sensor systems to image plants/ crops, and accurately navigates between them to perform specific tasks, thanks to open skies, besides adding to the traceability or quality control of harvested products [3].
In agriculture and forestry though, inaccuracies in position and directional information lead directly to economic, productivity and environmental losses. Crop parcel zones may not be harvested, requiring a “second pass”. Crop collection after a navigation error also requires a “second pass” which costs manpower time, machine time and fuel. Residues may be generated at higher rates lowering yield and eventually leading to environmental problems over some time. Nevertheless, such economic impacts of GNSS kinematic inaccuracies are rarely even considered, even if they should in the overall trade-offs between system performances, manpower costs, equipment usage time, and high investment costs of precision farming equipment [4].
Narrowing down our focus now onto the effects of inaccuracies affecting forestry operations, GNSS accuracy is already considered sufficient in some specific forestry uses such as those for chippers, trucks, guidance to visitors, and location of storage and landings [5].Coupled to wheel rotation sensors, Differential GPS (DGPS) allows to estimate wheel slippage in uneven forest terrains [5]. Areas insufficiently researched though are first the effects of GNSS kinematic errors on harvesting itself, as well as next on log collection and logistics.
Contrary to many other application areas, high accuracy mapping information in forestry is very often lacking, and even more so for individual tree locations. In addition, the harvester navigation using GNSS receivers requires an unobstructed line of sight (or sufficient signal/noise values) from the harvester trajectory points to a minimum of four satellites. This is often difficult to achieve in forest environments, as trunks, foliage can block the GNSS signal; furthermore the propagation is also affected by humidity, snow, and wind. Forest canopy can be characterized by means of parameters such as tree density and biomass volume, but it is important to know which parameters in particular have a bearing on the accuracy of GNSS measurements. Canopy density can be evaluated by LIDAR pulse density [7], imaging spectroscopy, or vertical structure profiles (as Plant Area Volume Density, PAVD), all of these techniques being costly and sometimes slow. In view of the complexity of forest environments, propagation effects, and signal outages, some research has dealt with refined algorithmic approaches (eventually coupled to inertial navigation systems) to estimate the accuracy of individual GNSS positions [8-10]. Vertical measurement accuracy by GNSS has also been studied in [11]. These results show that the highest impact on the positional accuracy is from the forest canopy.
GNSS data from the harvester can be combined with a laser-rangefinder (lidar), or laser scanners, serving to determine the tree trunk position and diameter [12]; laser sensors determine distance and angle information to determine the presence, range and diameter of a stem before it is cut. However, they are of no use once the stem has fallen, and this is where the robotic harvester with GNSS investigated in this paper steps in.
In this paper we contribute experimental findings to the issue of the accuracy of GNSS location measurements in forest environments, by addressing the effects of harvester trajectory errors due to GNSS measurements. The deployment context is GNSS assisted [13] or GNSS robotic guided dynamic forest harvesting [14] where a process-linked sequence of relative positions and directions between the harvester and a fallen tree translate into harvesting yield. In future generation harvesters, the harvester will have its own integrated GNSS receiver, coupled to a data acquisition and to a communications module; the harvester will operate either in an assisted mode, or in an autonomous navigation and harvesting mode.
In an assisted mode, the data (operation speed, location, harvested yield, machine settings, knife drum speed, engine and motor alarms) are transferred from the harvester to a remote control system, reducing manned operator workload while exploiting, if available, mapping [15] and other Forest Management centers’ information. The harvested area can be characterized in real time from the field patterns registered by the GNSS system on the harvester, for later use in log recovery and logistics.
In a robotic operational mode, the harvester makes autonomously navigation decisions to maximize productivity and harvesting revenue. The forest product industry is maximizing the combined value and quality of timber logs, and secondary products, while minimizing the volume and handling of residues. As shown in [16] it is possible to gain significant profit margins when having full certainty about the tree attribute and quality information.
2 Research questions
As discussed above, one specific class of restrictions on robotic harvesting comes from how the terrain and canopy combined limit GNSS signal quality and thus location and trajectory accuracy. This is especially true of forestry in rugged terrain, dishomogeneous tree growth, high canopies and wet/snow covered foliage. This paper is specifically dealing with forestry operations with robotic or assisted harvesters, taking into account the maneuvers, relative positions or directions, and trajectories.
The research questions which were studied experimentally and by modeling are:
Research Question 1: how much are location and directional accuracies of GNSS signals degraded in forests, compared to the operational capabilities and kinematic requirements of future precision forestry harvesting?
Research Question 2: how approximately is the forestry harvesting yield affected by GNSS signal accuracy in forestry environments, so a trade-off can be made between harvesting by manned resources vs. costlier autonomous equipment?
3 Real time estimates of effects of canopy opacity and precipitation
This Section analyzes in more detail some effects linked to Research question A: water retention in foliage (Section 3.1), electromagnetic propagation aspects (Section 3.2), and opacity determination by real-time image processing (Section 3.3).
3.1. Vegetation based interception
Interception is defined in the present context as the process of retaining rainfall water on the whole surface of a plant. The amount of water retained depends mainly upon the size of the tree’s surface, and upon the potential influence of species [22]. The adhesion and retention of water droplets on leaves and needle surfaces depends also upon the surface state and even upon the temperature of the rain water [23]. The biggest amount of water from rainfalls may accumulate in tree crowns at low rainfall intensities and for smaller raindrops. The maximum water absorption capacity of tree crowns is a not constant value: it changes under influence of rainfall characteristics [22]. As a result, the GNSS electromagnetic propagation in and around canopies depend from botanic properties and these rainfall characteristics.
3.2. Electromagnetic propagation aspects
First, forest canopy absorption affects the GNSS signals used to determine the harvester position. This interference is difficult to study by GNSS interference instrumentation [38]. Second, leaves and foliage worsen multipath effects; this in general eliminates Differential GNSS (DGNSS) relevance. A third effect has to do with water retention by the canopy after rain or snow (see Section 3.1.); this is difficult to model by propagation theory as the water content is both on and in the leaves and depends on local hydrological conditions; leaves also release water vapor which can have a far stronger impact on the GNSS signal than the liquid water content. Figure 1 (from [24] using [25]) gives the microwave scattering spectra in snow and rain for GPS broadcasts in two L-band signals at 1575.42 MHz and 1227.6 MHz from an orbit of roughly 20200 km. They show that liquid water doesn’t typically interact strongly with L-band signals or anything below 15 GHz. The fourth effect is linked to the tree species; in some regions for example Pinus Sylvestris L. (pine) needle length approximates one wavelength of GPS L1 signal. As a result of all these four effects, in the remainder of this paper we refer to the combined opacity degradation from multipath, refraction, attenuation and blocking.
3.3. Real time opacity estimation by image processing
Earlier research in the context of rain forests has shown that high canopy opacity affects GNSS signal strength and thus positional spatial error (typically 10-30 meters for GNSS and spotwise 1-5 m for Differential DGNSS [17]). Indeed there is no way from under the canopy to detect under/over 15 degree elevation GNSS satellites. To alleviate this, one obvious approach is to raise the GNSS antenna above the canopy [26], but this is hardly feasible for moving forest harvesting equipment. Some research has gone into long GNSS signal acquisition times/ numbers or epochs to improve positioning accuracy [17, 27] but this is hardly compatible with real harvesting operations where the harvester roves around. In view of real time acquisition requirements on harvesters, and moving satellite positions, high accuracy LIDAR biomass estimation and stand density (in stems/ha), and SAR are not relevant either, except LIDAR to select individual trees or patches of trees. Rather than optimizing GNSS receiver designs [27], which is bound to be very specific, the approach taken here is to exploit in the best possible way GNSS receiver signals, by compensating them after correlation analysis, with other real-time measurements. Options include: Kalman filtering combining GNSS / opacity sensor measurements, or to calibrate error estimates, or in safety cases to generate an alarm and switch off temporarily GNSS signal driven navigation commands to the robotic harvester. The specific opacity sensing approach used was to capture in real time, in most radial directions and at all elevation angles, digital fish eye images from the moving harvester roof. The median and average of the histograms of the fish eye radial images were computed, and each such image turned binary at the histogram’s mean value, showing canopy, branch and leaves’ obstruction in black and open day-time sky in white. The lower the average gray level of the binary image, the higher the obstruction measured in black pixels. Simple regression allows determining the opacity level beyond which GNSS inaccuracy is too high for the harvester to generate robotic movements. It should be pointed out that the use of a camera and of image processing as described do not necessarily represent an addition of the instrumentation of the forest harvester, as these two items may have a parallel use in determining the machine’s tilt angle, thus providing redundancy to GNSS based estimates of the same (see next Section 5) [28]. For the sake of clarity, it is pointed out that the results in the following Sections were obtained without use of this opacity sensor, as emphasis is solely on kinematic GNSS derived errors, thus already opening an alley for improved results by the approach above.

4 Harvesting dynamics and robot harvester
In order to lay the basis for kinematics, Section 4.1 summarizes the traditional harvesting process and its phases, while Section 4.2 adapts it to robotic forest harvester design and operations and gives details of the kinematics assumed in Section .
4.1 Present day forestry operations
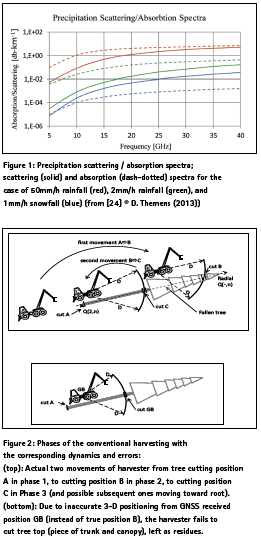
In present generation man-operated harvester operations Figure 2), the canopy is not cut off first. In a Phase 1, the whole tree (stem) is cut close to root position P by the harvesterhead which is attached to the telescopic hydraulic arm (Figures 3 and 4). After the stem has fallen down in some direction, in a Phase 2 the branches are cut off (“delimbing process”) when the harvester head moves along the trunk from the bottom of the trunk to the top; the density of branches along this path obviously depends on the species.
In a Phase 3, after having cut the branches, the harvesting head moves back to P and cuts the stem into logs and ends at the top [31-32]. An algorithm, outside the scope of this paper, may optimize the cutting of stem to logs. The tree may have been selected in advance from its location by airborne laser scanning which may even provide an estimate of individual tree volume [33].
4.2 Robotic harvester operations
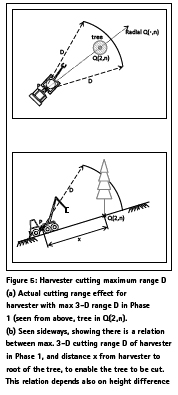
In this paper, we are concerned with GNSS equipped robotic harvesters, which once brought to a forest location, tackle autonomously one tree after another (identified and located by a simple laser scanner) , under possible supervision of the logistics people, so that harvesting and collection can happen at the same time with one single operator. Knowledge of errors in absolute coordinates are then of course of importance. The harvester carriage has a hydraulically movable sawing/ cutting head with a maximum range D in polar coordinates (Figure 5). Current manual harvesters and log grabbers have maximum ranges D of approx. 10 meters, due to moment of inertia constraints when lifting and conveying logs. In this paper, the robotic harvesters are supposed to be devoted only to cutting, for which the heads (Figure 3) are much lighter, and the maximum ranges D can therefore reach 20 m or more (alike nacelles and many civil engineering equipment’s).

The single trees are identified and located by a simple ultrasonic or laser sensor, or when the operator brings the robotic harvester close to the first tree. As in general individual tree location, extent and volume are not known (or require extensive and costly 3D laser mapping, plus a lot of 3D image processing), the robotic harvester just cuts when it is in polar radius range (combined distance and height) of a stem , using only GNSS data and the same dynamics as the traditional method. This is why GNSS height and directional inaccuracies are critical, in all Phases 1, 2 and 3 (Figure 2), while tilt is less. It is reminded that the focus in the present papers is on the GNSS derived trajectory inaccuracies.
In operations, as in our model, GNSS height inaccuracy affects Phase 1, in that a positive height error lets the robot believe it is higher than true, so stem is not cut at root/ soil level. Regarding the direction in which the tree falls in Phase 1, this can be roughly controlled by the harvester using current processes. In a robotic process, to minimize harvester moves, we suppose that in Phase 1 from position P, the harvester cuts the fallen trunk up to maximum of its 3-D range D.
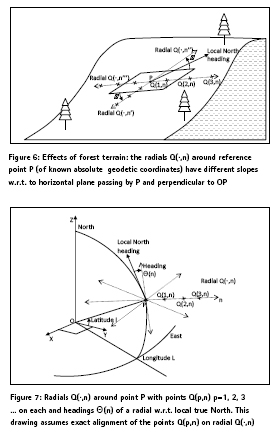
In Phase 2, a 2D range error and heading error may imply that some branches are no cut or not close enough to trunk direction. In Phase 3, the model accounts for a 2D range error, in that maximum log length is equal to saw range affected by GNSS range errors. The necessity to cut to length is also affected; to simplify the model assumes nominal log length to uniform and proportional to harvester max. range D in plane parallel to terrain. As the saw is mounted on a telescopic arm, the cutter movements are programmed to operate in phases 2 and 3 with minimum movements of the harvester vehicle. Terrain slope errors are accounted for in the model and determined from GNSS radial measurements (see Figure 6), but the polar movements of the telescopic arm compensate to some extent for these terrain slope errors, which in turn contribute to 3D radial distance errors. It should be noted that in operations, like in the model, there is a snow ball effect on errors as the sequence of Phases is fixed. The yield losses as estimated in each radial direction are thus a maximum, also because the robot harvester is assumed only to carry out once each Phase. It carries out only two movements limited to three locations: close to root P in Phase 1, within range of fallen tree top in Phase 2 to delimb the top, and within range of P in Phase 3. In reality, once a cycle has been carried out, the trunk presence sensor would identify remaining trunk parts still in soil, or non-cut trees.
We do not address any collection and transport processes, or cases such as steep terrains where a trunk cannot be pieced in forest: it is carried in one piece, and then cut outside the forest. Canopy is usually treated us a residue/ slash (branches and needles) and can be bounded by a slash bundler, or it can be chipped into chips before being taken out of the forest.
5. Methodology
This Section addresses two related methods, where the first one is devoted to a novel experimental characterization of kinematic GNSS accuracy taking relative position and directional information into account to address the harvester head trajectory; field results are collected from 3 forestry sites (A,B,C). The second method in turn uses a simplified volumetric forest harvesting model to estimate the loss of harvested trunk and canopy resulting from the previously measured GNSS inaccuracies at (A,B,C). It estimates the directional and cumulative yield losses of a semi-autonomous harvesting machine cutting branches and logs at locations (A,B,C). In the specific case of the plantation C, the preferential direction of harvester movement is the heading of the plantation rows.
Section 5.1. gives details on the experimental parts, Section 5.2 on tree metrics used in the model to measure trunk yield, and Section 5.3 on the measure of canopy yield, the last two combined into an average yield loss discussed in Section 5.4.
5.1. Experimental methodology
In real forests, as positional accuracy and directions are the key criteria to enable the correct positioning and volumetric cutting by precision machinery (see Section 4), what matters is the distribution of absolute positioning errors produced by the GNSS driven actuators over the work area around say a given tree, and the cutting direction accuracy from different angles (or down an alley in a forest plantation). Therefore, the probability distribution of the 3D GNSS errors must be estimated on a radial grid around the target location P (see Figure 7) representing a tree base. In the field data collection, the minimum angular resolution of the radial grids has been taken to be 45 degrees, and each radial direction must have at least 3 GNSS measurement points. These radial measurements are a novelty of this paper.
By considering the errors along the radials and the altitude, it is possible to assess the kinematic positioning error effects. As shown later, because true deviations to geodetics are determined, and because geodetic information is not available in 3D-space, a sampling is carried out along the radials. Some theoretical research has tried to advance the concept of simultaneous localization and mapping (SLAM) [36] [37], but this is highly unrealistic as most forests do not have absolute 3D mapping references for the trees, nor relative high accuracy mapping information. Horizontal lines of sight beyond short ranges for geodetic lasers in forests are in almost all cases more obstructed than vertical ones.
Another variable is the mix of species especially in natural forests which do not have the better homogeneity of plantations. The reason is that the absorption properties of leaves, branches, differ between tree species in the GNSS frequency bands and affect the polarization as well (see Section 3.2). Therefore, the experimental data collection methodology had to be replicated across the different forestry environments (A, B,C) , with Picea abies L. ( spruce) and Pinus Sylvestris L. (pine) taken as opposing sample cases. They also have quite different canopy height profiles, with as extremes a quasi-complete canopy coverage of the sky above the forest (site A), to quasi- omnidirectional satellite visibility in low density forests (site B), to satellite visibility in plantations with uni-directional tree lines (site C).
To measure the relative canopy opacity and extent, fixed aperture digital imagery (Section 3.3) was collected at (A,B,C). Histogram analysis was carried out by digital image processing, to determine the mean and median levels of the gray levels between full opacity (level: 0) and maximum luminance (level: 255). The lower the mean or median, the more opaque the canopy, as shown on the corresponding binary images after thresholding at the median gray level.
Finally, humidity and water retention of the tree volumes and foliage may play a role in the GNSS signal absorption (see Section 3.1), so measurements had to be done under different meteorological conditions (site C).
The above criteria, plus the availability of absolute geodetic coordinates (which are rare in forests) have led to the following selection of GNSS accuracy measurement sites in the following three different forests:
-Location A: Coordinates E19, 065115 N49,676595 Altitude:717 meters, Lipowa Forest District, Poland: Complete canopy 40 m high, high density mixed Picea abies L. (spruce) (75%) and Pinus Sylvestris L. (pine) (25%) natural forest in exploitation, on slightly inclined irregular terrain. This terrain is in a way similar to the one studied in [17].
-Location B: Coordinates E19,03135 N49,69182 Altitude:1257 meters, Skalite Forestry District, Skrzyczne, Poland : Low density forest in exploitation on a rather flat hilltop area, with mostly Pinus Sylvestris L. (pine) ; such an area also has similarities with areas which have been devastated and which must be recovered; trees are from 5 to 20 m high.
-Location C: Coordinates E 20.3754018206 N 50.0519851297 Altitude: 191 meters, Niepolomice Forest, Poland: Old 100 year 80 % Pinus Sylvestris L. (pine) forest analyzed in a radial area, but also between two plantation roads, in a rather flat area; measurements were carried out during a rain spell with rapid humidity build-up; trees were 25-50 m high.
The exact locations of these specific three geodetic surveying points are known with an accuracy of 1 cm guaranteed by the Polish geodetic survey, with physical markers in the ground. At each exact location (A,B,C), a theodolite was placed to generate minimum 24 marker points in 8 radial directions spaced 45 degrees with known ranges and inclinations; the ranges and alignments were verified by a laser rangefinder of 1 cm accuracy. In this way, a radial grid of minimum 24 marker points with known absolute coordinates was generated around each location. The inter-marker point distances varied by site due to terrain conditions, but were in the 5-8 m interval.
At each marker point, a commercial high precision aviation GNSS receiver was placed (see Appendix), to record UTM [18] values, elevation, satellite numbers in sight with relative signal intensities over 100 seconds. The measurements were repeated for both horizontal and vertical antenna polarizations. Measurements from additional GPS receivers were recorded at the reference points (A, B, C) for comparison.
By comparing the absolute marker point coordinates in the radial grid, with the GNSS measurements at each, the 3-D GNSS accuracy distribution could be recorded on the grid, and put in explicit relation with both GNSS satellite coverage and tree opacity.
To adopt a geode model [19] likely to be found in GNSS receivers used in harvesting equipment, the geode selection made was WGS84.It should be added that many geodetic administrations, including Poland, offer more accurate geode models giving increased GNSS accuracy.
The 24 GNSS 3-D error measurements over the radial grid are fit with a best explicit continuous matching function. Current mathematical tools allow the fitting error criteria to drive the selection of the parametric fitting function from a wide diversity of options, as opposed to older approaches where the tool user had to choose one fitting function. Note that this continuous matching allows extending the present analysis to the whole neighborhood of the stem location P, instead of just averaging some finite locations.
5.2 Tree harvesting metrics
We shall use in the model the diameter at breast height (DBH), which is the measurement of a tree’s girth standardized at 1, 3 meters above the ground. Also a tree cone model is described, which can be related to the form factor defined in forestry science ; the form factor indicates the shape of the tree based on recorded trees of different species and commonly given for calculating tree volumes for a given species. It is usually related to DBH and age class. Could also be used in this tree cone model the tree taper, which is the degree to which a tree’s stem or boles decrease in diameter as a function of height above ground. The tree volume was calculated from the metrics recorded in a plot sample from the Polish Forest Administration Authority, or using tables such as those by Pollanschütz [20]:
Tree-volume= BA * Height * Form-factor (Equation 1)
where:
BA: area of the base at a designated height (such as 1.3 m),
H: full height of tree,
F: is the form factor shape of a tree trunk.
It is pointed out that when airborne laser scanning data are used, errors affect the estimated tree height and tree volume as derived by Equation 1 [21].
5.3 Canopy harvesting metrics
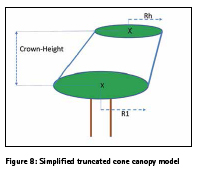
To estimate canopy harvesting metrics, the simplified canopy volume model used is a truncated cone with two parallel circular bases, sitting on a trunk of a given height (see Figure 8). This crown volume is (note that this formula holds even if the crown is tilted):
Crown-Volume= (π. Crown- Height/3) (R1**2+Rh**2+R1*Rh) (Equation 2) where: π: constant
Crown-Height: height of exploitable crown from top point of tree trunk
R1, Rh: radii of horizontal crown sections at extreme ends of the cone
5.4 Average yield loss
It is reminded that we do not assume the robotic harvester to be equipped nor assisted by stem height sensors. To simplify, the algorithm by which the stem is cut into logs, is assumed to be equal log length, as a consequence of the fact that geodetic -to-GNSS deviations can only be measured at equal ranges around each radial, and that the log length must therefore be equal to this range.
The localized yield loss is then the weighed sum of the average trunk volume not cut due to GNSS positioning errors, and of the crown volume not cut, for one range and one direction. Users can determine the weights in relation to processing time or costs. This yield loss is integrated over all relative radial distances and cutting directions of the harvesting machine, using the GNSS error best matching surface function of (x,y,z) (Section 5.1) :
Average-yield-loss= ∫ (interval of Θ) ∫ (interval of ρ) [w1. Crown-Volumeloss+ w2.Trunk-volume-loss] dΘ.dρ (Equation 3)
where: -Θ: cutting / harvesting direction, subject to GNSS measurement inaccuracies (see Section 6);
-ρ: distance of harvesting machine to tree root P, subject to GNSS measurement inaccuracies (see Section 6); its maximum value is D.
6. Static and kinematic GNSS inaccuracies impacting harvesting
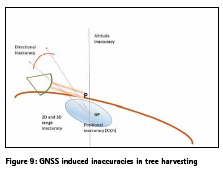
A GNSS error in a radial direction means that a cutter will either cut too much or too little. A GNSS error in position means that the saw supposed to cut the trunk, will be too close or too far from trunk. GNSS elevation errors imply that too little / too much of trunk is cut, affecting the number and lengths of the logs; it is reminded that in this study we do not assume corrections by a laser scanner. Repeated movements of the harvester result from these combined errors and vastly reduce productivity. These inaccuracies are summarized in Figure 9. Section 6.1 gives the exact definitions used for the GNSS inaccuracies, illustrated by figures. Section 6.2 operationalizes these definitions in the context of harvesting, and Sections 6.3 and 6.4 report the experimental findings collected as explained in Section 5.
6.1. Definitions
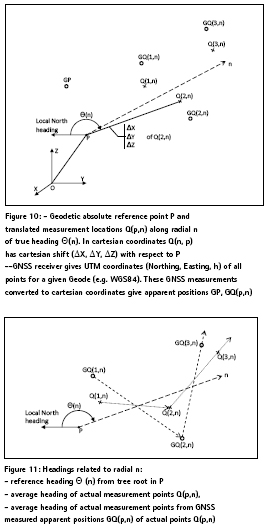
As shown in Figure 10, the radial GNSS measurements GQ(.,n) are carried out around a geodetic reference points P, along several radials n at the “real” geodetic marker points Q(.,n). Whenever possible, at least 3 points were chosen along each radial n, in such a way that the range from P to the furthest point, say Q(3,n), was at least equal to the maximum range D by which the telescopic arm of the robot harvester can cut (see Figure 2). In this way the 3-D radial distribution of GNSS inaccuracies could be measured within the robot harvester’s operating range when it is supposed located at P.
The coordinate transforms of all points Q(.,n) and GQ(.,n) used the high accuracy algorithms used by the US Federal Communications Commission and Federal Aviation Agency [29].
6.2. Geodetic marker points and GNSS inaccuracies
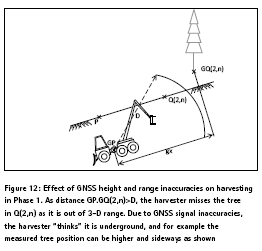
The theodolite, placed above geodetic reference point P, allowed precise range, tilt and azimuth determination, leading to the Cartesian coordinates for each of the marker points Q(.,n) where GNSS measurements were carried out; account was of course taken for the height shift between the theodolite optical turret axis and physical reference point P in the soil. The GNSS measurements were carried out by placing the professional GNSS receiver on a platform exactly at these marker points Q(.,n), yielding a set of measurements at GQ(.,n) after 100 s satellite acquisition (Figure 9): UTM coordinates at GQ(.,n), altitude at GQ(.,n), and signal strengths of all satellites in view leading to these measurements. The process was repeated twice at each point, with respectively horizontal and vertical GNSS receiver polarizations. The GNSS inaccuracies were determined in UTM and altitude coordinates by taking the differences between measured GQ(.,n) coordinates and true marker Q(.,n) coordinates. Subsequently, planar 2D and spherical 3D positional errors were computed, as well as the robotic harvester’s heading errors along each radial direction n, taking the GNSS derived heading to be the vector from GQ(1,n) to GQ(3,n) (Figure 11).
It is here necessary to recall (see Section 4) that the direction in which a stem falls after being cut above the root, is the physical effect driving the need to characterize GNSS inaccuracies in radial directions; this effect is compounded with the effect of varying forest terrain slope in different directions, so the radials cannot be treated as planar in a plane passing by P. In this way, one must characterize the GNSS inaccuracies from the radial distribution of positional, range as well as directional errors, as a robotic harvester would encounter them when working on a tree with a physical root in P. Figure 12 shows the implications of these errors, first in general, then on where the harvester perceives the fallen trunk to be in 3D space, and finally on the missed or erroneous cuts on the trunk and canopy.
7. Experimental harvester trajectory inaccuracy results
7.1. GNSS inaccuracy results
In general, the GNSS inaccuracies, despite varying foliage and humidity conditions, demonstrate average values over the radial directions, which are compatible with robotic harvester arms of max. length D<20 m and with a carriage heading variability of +/- 20 degrees. In heavy foliage and on slopes like in Forest A, the corresponding extreme values of the inaccuracies in some radial directions, do not meet these compatibility criteria; the extreme values are about double those for open terrains like Forest B. Errors in high tree forests, such as Forest C, match those in Forest B, including for heading errors of approx. 10 degrees. In high tree forests and in rainy conditions, some errors are extremely high for short periods of time. The height errors are probably the one’s the most exposed to canopy density. However, these GNSS kinematic inaccuracy results are misleading in harvesting yield terms, because many factors interact with them to determine such yields (see Section 8). Comparative GNSS error data for much easier agricultural fields are provided in [30].
7.2. Effects of rain and water retention in foliage
The experimental plan included GNSS measurements under rainy conditions in Forest C. They were limited to one radial direction where the Norting and Easting errors were huge, combined with the high canopy, during the intense rain pouring phase. The corresponding values were excluded from the analysis, subject to stating the rule that a robotic harvester anyway normally would halt its operations under such weather conditions. All other measurements in Forest C and its plantation row were under wet foliage conditions; at this stage we can conjecture that stronger multipath scattering is producing larger extreme values on the GNSS measurements, but does not degrade average errors (see Table 1).
8. Model and estimates of the implications of gnss kinematic inaccuracies on robotic forest harvesting average yield
As highlighted in above Sections 5 and 6, GNSS inaccuracies have a direct impact on the relative true positions of a robotic harvester navigating according to GNSS measurements only. But, on the other hand, the flexibility of the cutting arm of the robotic harvester (on wheels or tracked wheels) can, in some relative positions, compensate for GNSS inaccuracies. Also the GNSS navigation allows the harvester to optimize its movements to minimize total processing time per tree. The combined result of the two effects is a possible loss in exploited stem length, and in the fraction of the canopy being harvested, compensated by fewer carriage movements; this paper proposes a simple model to estimate these combined effects.
Section 8.1 gives the tree species and robotic harvester attributes used in the model. Sections 8.2 to 8.5 detail the kinematic effects in due to the harvesting process sequence. Finally, Section 8.6 provides the average yield implications of the GNSS kinematic inaccuracies reported in Section 7.1.
8.1 Tree species and robotic harvester attributes
Essentially, the model estimates the impacts of GNSS kinematic inaccuracies when harvesting a single tree, rooted at position P in a forest, and to which the robotic harvester has navigated aided by a laserscanner (assumed error less). This tree may belong to a variety of species, for which are given the average trunk radius, trunk height from root, canopy height and canopy radius (see Section 5.2). The canopy is considered homogeneous in terms of marketable residues and the harvested volume is taken as the harvested fraction of the conical canopy (see Section 5.3). As a simplifying assumption, the canopy shape is taken to be a full symmetrical circular cone (Rh=0 in Equation 2) placed on top of the tree trunk. The tree to be harvested has a root in point P for which exact geodetic coordinates are known. The robotic harvester is characterized by the maximal radial length D of its telescopic arm, at the tip of which is the hydraulic activated cutter. This telescopic arm is positioned at the front of harvester at a parametric guard distance from the geometric center of the wheels. It is assumed that the robotic harvester can only cut by mechanical design and balancing conditions at points higher or equal to itself.
8.2 GNSS Positional errors of robotic harvester
As the harvester will move along the fallen trunk (Figure 2), in a way and along radials n as explained in Section 4.2, we make the approximation that the positional, range, tilt, and directional errors (see details and experimental data in Section 7) are those at points Q(2,n) located at about midrange of the telescopic arm (Figure 10) .
8.3 Phase 1 trunk cutting phase
When the tree is cut at root level (or above it due to elevation errors) in location P, it will fall in a direction n, taken now as random with equal distribution across 360 degree radial directions. At this stage, terrain slope effect on the falling direction n is not taken into account.
The model assumes the harvester to be in the perceived GNSS dictated GP position (different from geodetic P) (Figures 9, 12), trying initially to cut from there in one pass. This produces a log length eventually shortened by both the positioning error about the root at GP where the tree was cut first (in this especially the GNSS elevation error plays in (Figure 12)), and the positioning error in the upper part of trunk, if this is reachable within range D. E.g. if harvester thinks it is higher than truth, the lower part of trunk is not cut and stands on the ground. The reachability condition accounts for the 3D GNSS radial error (as tree is fallen, but top may be higher/ lower than P due to terrain). If max. range D is sufficient, a part of the canopy is cut at the same time. The metrics at the end of Phase 1 are the cut trunk length and the cut conical canopy slice height; these are determined from the GNSS measurements for all individual radial directions n into which the tree may have fallen.
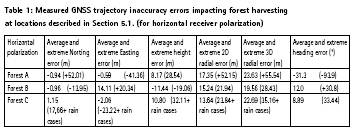
8.4 Phase 2 canopy cutting
Because of the GNSS induced twodimensional radial errors, the outreach of the telescopic arm working at ground level where the tree lays in direction n, is not the maximum D, but possibly less. We assume the actual outreach, in Phase 2 in direction n, to be D minus the root mean square of the twodimensional radial errors at point Q(2,n).
If the harvester cannot reach the canopy from its initial position in P (perceived as GP), it will move a minimum along direction n to where trunk was cut in Phase 1 at maximum range, and try to cut through canopy from there. The exploitable part of the canopy which gets cut is a fraction of the conical canopy volume (see Section 5.3). The most remote part of the canopy and sometimes all of it, which did not get cut in Phase 2, remains on the ground and is left as residue considered non-exploitable in the model.
8.5 Phase 3 log cuts
In Phase 3, the robotic harvester moves in the perceived radial direction n (subject to GNSS induced heading error), and is programmed to move just enough in radial direction n to cut, if necessary, the trunk into equal logs equal to a fraction of maximum range D. These are determined for all radial directions n using the GNSS inaccuracy measurements. Obviously if total tree height is less than D, and fraction is 100%, there will only be one log piece, and the harvester will not have to move and thus does not have to be exposed to GNSS heading errors when cutting the trunk, but only when cutting canopy. In most other cases, or when log fraction length of D is small, the harvester will continue moving in the perceived radio direction n.
8.6 GNSS error implications on harvesting yield
From the above results, the model determines the cut trunk volume, the cut exploitable canopy volume, and the losses on both compared to the full tree resources (Sections 5.2-5.3). These attributes are averaged over all possible 360 degree directions into which the tree may have fallen.
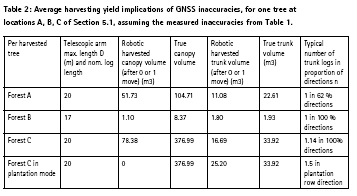
The analysis of the model results show that trunk volume yield in dense foliage areas such as Forests A and C are about 50 %, and less for exploitable canopy products, with missed wood resources in 38 % of directions for lower trees (Forest A) and none for higher trees (Forest C). The loss of trunk volume in sparsely covered areas, such as Forest B, is minimal (less than 6 %) even with shorter telescopic arms, but 80 % of exploitable canopy resources are lost due to radial GNSS errors. Trunk volume yield in plantations, such as the plantation row in C, are excellent with 75 %, at the expense of very low canopy yield; log lengths are excellent,
In these three forest cases, and for the chosen parametric values, the harvesting operations (excluding logistics) proceed very fast, with at most one move of the robotic harvester, which opens up for significant total harvesting productivity gains in time compared to operator driven machines.
Operator driven just like robotic harvesters must both still be moved from tree to tree, with or without laser scanner positioning, so this displacement effect is equal, with no advantage to manual or robotic harvesters if the robotic harvester is equipped with a simple tree location determination device.
9. Robotic harvester productivity & economic impacts
Logs are priced by the length and width; canopy biomass is priced according to a calculation connected to the trunk (canopy volume). Usually canopy slashes or residues stay at felling site and are mixed with soil, but some machines collect them [32]. The model of Section 8 produces other interesting results than harvesting yield of robotic harvesters operating on the basis of GNSS receivers. We can summarize as follows the additional productivity and economic consequences on the harvesting process:
Harvesting equipment usage time is shorter with robotic harvesters because of the embedded navigation system and optimized trajectories (see Section 4.2). The compromise is to be achieved in trajectory planning between the number of passes/cycles for a given tree in average, as harvesting yield goes up with the number of passes, but then equipment usage time goes up as well ;
Less movements are needed by the robotic harvester with very few only per tree (if cutter max. range D is adequate for the harvested species). Table 2 shows that an acceptable average yield is already achieved after just no or one carriage move, after finding tree, even if “second passes” may be necessary. Harvesting yield and adequacy of log lengths go up with the number of passes, but the number of carriage movements and their duration then go up (together with cutter usage time, and fuel);
One of the robotic harvester’s drawbacks as shown in Table 2, is the loss of branches/ biomass not harvested / cut; as this resource is treated as low value residue, the economic loss is small, but can be higher in an environmental sense. iv. Another drawback is on lost value from trunks cut at wrong length; however it is unclear what price dependency there is to length vs. diameter, and the main effect may be higher variability of harvested log lengths. The information collected also has an impact, especially when supported by IT tools, as explained in [34]. Nevertheless, such productivity and economic impacts of GNSS kinematic inaccuracies are rarely even considered, even if they should, in the overall tradeoffs between manpower costs, equipment usage time, and expensive precision harvesting equipment investments.
10. Future directions
A subsequent paper will analyze the GNSS signal strengths and real time image processing opacity measurements, and yet another, the effect of water retention in foliage in relation with signal strengths.
In the meantime, one may question if GNSS receivers to help the navigation of robotic harvesters can be replaced by other positioning technologies. One traditional avenue which has been considered is the use of Differential GNSS positioning such as provided by DGPS receivers. However this approach is far from straightforward as the propagation, multipath, and humidity effects will vastly increase, risking even to increase positional error variability. Another avenue is to combine a GNSS receiver with a low cost inertial navigation system (INS) or with optoelectronic guidance and range finding. However, in forestry, it is likely that high levels of vibrations and shocks will preclude most INS, except high cost fiber optic INS.
In the future should be envisaged how unmanned flying vehicles (UAV) equipped with higher precision GNSS receivers (including DGPS and equivalent) could work in formation with forest harvesting equipment to increase their accuracy during lapses of insufficient accuracy of on-board harvester GNSS receivers. UAV already helps provide tree height information [35].
11 Conclusions
•Research question 1: Location, range and directional GNSS derived information are degraded in forests; GNSS positioning in some categories of forests as identified in this paper may be sufficiently accurate for automatic forest harvesting, except under rain conditions.
•Research question 2: Even assuming a very simple stem-to-log cutting algorithm, and no stem height sensor, recovered trunk volume is good enough, contrary to recovered canopy volume, to justify robotic harvesting, especially in view of increased time based productivity. Issues remain around the exploitation and pricing from logs with higher variability.
The addition of different robotic harvester-born sensors, on purpose not taken into account in this study (e.g. lidars, real time imaging opacity measures), will strengthen these conclusions. It is also to be noted that if GNSS is the fall-back navigation system in case of the likely frequent failures of optoelectronic sensors on high vibration harvesters, the above conclusions stand.
References
[1] Krüger G., Springer R., Lechner W. 1994. Global navigation satellite systems. Computers and electronics in agriculture 11(1): 3-21
[2] Unknown .2014. La ferme des robots. Valeurs actuelles 20 March 2014 : 52-55
[3] Falkenstein P. 2012. Multispectral imaging plants roots in quality control. Vision systems design Dec. 2012: 23-25
[4] US Congress. 2015. Major uses of GPS and economic benefits. Washington D.C.: US National executive committee for space-based positioning, navigation and timing (PNT)
[5] Sikanen L., Asikainen A., Lehikoinen M. 2005. Transport control of forest fuels by fleet manager, mobile terminals and GPS. Biomass and Bioenergy 28( 2): 183-191. ISSN 0961-9534, http://dx.doi. org/10.1016/j.biombioe.2004.08.011
[6] Ringdahl O., Hellström T., Wästerlund I., Lindroos O. 2012 .Estimating wheel slip for a forest machine using RTK-DGPS. Journal of Terramechanics 49(5): 271- 279. ISSN 0022-4898, http://dx.doi. org/10.1016/j.jterra.2012.08.003
[7] Jakubowski M.K., Guo Q., Kelly M. 2013. Tradeoffs between LIDAR pulse density and forest measurement accuracy. Remote Sensing of Environment 130: 245-253. ISSN 0034- 4257, http://dx.doi.org/10.1016/j.rse.2012.11.024
[8] Ordóñez Galán C., Rodríguez-Pérez J.R. , Martínez Torres J., García Nieto P.J. 2011. Analysis of the influence of forest environments on the accuracy of GPS measurements by using genetic algorithms. Mathematical and Computer Modeling 54(7– 8): 1829-1834. ISSN 0895-7177, http:// dx.doi.org/10.1016/j.mcm.2010.11.077.
[9] Adusumilli S., Bhatt D., Wang H., Devabhaktuni V., Bhattacharya P. 2015. A novel hybrid approach utilizing principal component regression and random forest regression to bridge the period of GPS outages. Neurocomputing 166: 185- 192. ISSN 0925-2312, http://dx.doi. org/10.1016/j.neucom.2015.03.080.
[10] Wezyk S.M. P. 2013. Pomiary GNNS w przestrzeni lesnej przy wykorzystaniu roznej klasy odbiorkikow oraz wybranych trybow pomiaru (in Polish) (GNSS Measurements in forest environments using various receivers and measurement modes. Archiwum Fotogrametrii, Kartografii i Teledetekcji 25: 217-231
[11] M.G. Wing, J. Frank (2011), Vertical measurement accuracy and reliability of mapping-grade GPS receivers, Computers and Electronics in Agriculture, Vol. 78, no 2, September 2011, p. 188- 194, ISSN 0168-1699, http://dx.doi. org/10.1016/j.compag.2011.07.006.
[12] J. Kalliovirta, J. Laasasenaho, A. Kangas (2005), Evaluation of the Laserrelascope, Forest Ecology and Management, Vol 204, no 2–3, 17 January 2005, p. 181-194, ISSN 0378-1127, http://dx.doi. org/10.1016/j.foreco.2004.09.020
[13] C. Amiama, J. Bueno, C.J. Álvarez, J.M. Pereira (2008), Design and field test of an automatic data acquisition system in a selfpropelled forage harvester, Computers and Electronics in Agriculture, Vol 61, no 2, May 2008, p. 192-200, ISSN 0168-1699, http:// dx.doi.org/10.1016/j.compag.2007.11.006.
[14] K. M. Bayne, R.J. Parker (2012), The introduction of robotics for New Zealand forestry operations: Forest sector employee perceptions and implications, Technology in Society, Vol 34, no 2, May 2012, p. 138-148, ISSN 0160-791X, http://dx.doi. org/10.1016/j.techsoc.2012.02.004.
[15] L.F. Pau (1990), Mapping and spatial data structures for navigation, ASI Series, Springer Verlag, Heidelberg ISBN: 3642842178
[16] M. Bedarul Alam, C. Shahi, R. Pulkki (2014), Economic impact of enhanced forest inventory information and merchandising yards in the forest product industry supply chain, Socio-Economic Planning Sciences, Vol. 48, no 3, September 2014, p. 189-197, ISSN 0038-0121, http:// dx.doi.org/10.1016/j.seps.2014.06.002.
[17] R. Valbuena, F. Mauro, R. Rodriguez- Solano, J.A. Manzanera (2010), Accuracy and precision of GPS receivers under forest canopies in a mountainous environment, Spanish Journal of Agricultural Research, Vol 8, no 4, p. 1047-1057, ISSN: 1695-971-X
[18] UTM, Universal transverse Mercator coordinate system, https://en.wikipedia. org/wiki/Universal_Transverse_ Mercator_coordinate_system
[19] D.G. Milbert, D. A. Smith (1998), Converting GPS Height into NAVD88 Elevation with the GEOID96 Geoid Height Model, National Geodetic Survey, NOAA, Washington D.C.
[20] J. Pollanschütz (1976), http://www. fs.fed.us/pnw/pubs/pnw_rp345.pdf
[21] P. Tompalski, N.C. Coops, J.C. White, M.A. Wulder (2014), Simulating the impacts of error in species and height upon tree volume derived from airborne laser scanning data, , Forest ecology and management, Vol 327, p. 167-177, DOI: http://dx.doi. org/10.1016/j.foreco.2014.05.011
[22] A. Klamerus-Iwan (2014), Different views on tree interception process and its determinants, Forest Research Papers, Vol 75, no 3, p. 291-300. DOI: 10.2478/frp-2014-0028
[23] K. Owsiak, A. Klamerus-Iwan, J. Gołąb (2013), Effect of current state of the sprinkled surface on rain water coherence: laboratory research on interception by trees,. Sylwan, Vol 157, no 12, p. 922-928
[24] D.R. Themens (2013), The quest for accurate 3D water vapor and temperature fields: a theoretical examination of the capabilities of a mesoscale microwave radiometer, MSc. Thesis Earth Sciences, Mc Gill University, Montréal, http://digitool.library. mcgill.ca/R/?func=dbin-jump-full&object_ id=119505&local_base=GEN01-MCG02
[25] F. Fabry, W. Szyrmer (1999), Modeling of the melting layer. Part II: Electromagnetics, J. Atmos. Sci., Vol 56, no 20, p. 3593 – 3600 http://dx.doi.org/10.1175/1520-0469
[26] N.J. Dominy, B. Duncan (2001), GPS and GIS methods in an African rain forest: applications to tropical ecology and conservation, J. Ecology and society, Vol 5, no 2, Art. 6, http:// www.consecol.org/vol5/iss2/art6/
[27] J.R. Rodríguez-Pérez, M. Flor Álvarez, E. Sanz, A. Gavela (2006), Comparison of GPS receiver accuracy and precision in forest environments. Practical recommendations regarding methods and receiver selection, Shaping the Change, Proc. XXIII FIG Congress, Munich, Germany, October 8-13, 2006
[28] J. Matej (2014), Determination of forestry machines tilt angle using camera and image processing, Computers and electronics in agriculture, Vol. 109, p. 134- 140 doi:10.1016/j.compag.2014.09.011
[29] Geotools and references www.apsalin.com
[30] F. Rovira, I. Chatterjee, V.S. Rubio (2015), The role of GNSS in the navigation strategies of cost effective agricultural robots, Computers and electronics in agriculture, Vol 112, p. 172-183 doi:10.1016/j.compag.2014.12.017
[31] Rottne Extreme Test – Harvester Extreme S2E5, https://www.youtube. com/watch?v=_vZyfa3D1QY
[32] Ponsse Ergo 8w Harvester in hard wood, https://www.youtube. com/watch?v=soLjGPknv2o
[33] P. Tompalski, N.C. Coops, J.C. White, M.A. Wulder (2015), Enriching ALS-Derived Area-Based Estimates of Volume through Tree-Level Downscaling, Forests, Vol 6, no 8, p. 2608-2630, DOI:10.3390/f6082608
[34] M. Carrascal, L-F Pau, L. Reiner (1995), Knowledge and information transfer in agriculture using hypermedia ; a system review; Computers and electronics in agriculture, Vol 12, p 83-119 ISSN:0168-1699
[35] P.J. Zarco-Tejada, R. Diaz-Varela, V. Angileri, P. Loudjani (2014), Tree height quantification using very high resolution imagery acquired from an unmanned aerial vehicle (UAV) and automatic 3D photo-reconstruction methods, European Journal of Agronomy, Vol. 55, April 2014, p. 89-99, ISSN 1161-0301, http:// dx.doi.org/10.1016/j.eja.2014.01.004.
[36] M. Miettinen, J. Kulosevi, J. Kalmari, A. Visala (2010) , New measurement concept for forest harvester head, in: A. Howard et al (Eds) , Proc. Intl. Conference “Field and service robotics 7”, Vol 62, Springer Tracts in advanced robotics, 35- 44 DOI: 10.1007/978-3-642-13408-1_4
[37] O. Lindroos, O. Ringdahl, P. La Hera, P. Hohnloser, T. Hellström (2015), Estimating the position of the harvester head: a key step towards precision forestry of the future?, Croatian Journal of forest engineering, 36(2), 147-164 ISSN: 1845-5719
[38] Z. Zhu, S. Gunawardena, M. Uut de Haag, F. van Graas, M. Braasch, GNSS Watchdog: a GPS anomalous event monitor, InsideGNSS, Fall 2008, Vol 3, no 7, 18- 27 http://www.insidegnss.com/magazine
[39] M. Petovello, How do you use GNSS to compute the attitude of an object? , Inside GNSS , Sept/Oct 2017, 36-39
Appendix: instrumentation used
-Zeiss Theodolite THEO 010-B ; -Leica Geosystems BSTO2L rangefinder ; -Laser technology TRUPULSE 360° B rangefinder ; Aviation GARMIN GPS receiver with WGS84 geode, two different antenna polarizations, signal strength measurements and some programmability features via FPGA ; Samsung Galaxy S2 Compass level from embedded magnetic MEMS sensors; -MAPPY E418 GPS receiver for planar coordinates
Acknowledgments
We greatly thank Mr. Marian Knapek and Wojciech Motyka from Lasy Panstwowe (Polish Forest Administration) from the Wegierska Gorka forest district for providing access to their forests, and geodetic information, and performing transportation of a team of six. Likewise, is greatly thanked the Krakow Forestry University for making available a team of post-doctoral field assistants (Mariusz Kormanek, Janusz Gołąb, Krzysztof Owsiak), lending extensive equipment and covering the local transportation costs to the remote forest districts (Department of Forest Engineering, Jarosław Kucza). The measurements were carried out as part of a Short term scientific mission under COST Action SaPPART by Prof L-F Pau, to the Krakow Forestry University, covering also the transportation cost for all the equipment brought from Denmark to Poland.
Permissions:Sole Copyright 2017- 2019 (C) to all authors , reproduced by permission of the authors to Coordinates, from (researchgate URL ) and EJPAU Electronic Journal of Polish Agricultural Universities, 2018 no 4, Vol 21(4), DOI:10.30825/5.ejpau.163.2018.21.4, EJPAU 21(4), http://www.ejpau.media. pl/volume21/issue4/art-04.html












 (1 votes, average: 2.00 out of 5)
(1 votes, average: 2.00 out of 5)





Leave your response!