| GNSS | |
Performance assessment of GNSS‑based real‑time navigation for the Sentinel‑6 spacecraft
GNSS-based onboard orbit determination can now reach a similar performance as the DORIS (Doppler Orbitography and Radiopositioning Integrated by Satellite) navigation system. It lends itself as a viable alternative for future remote sensing missions |
|
|
|
Abstract
The feasibility of precise real-time orbit determination of low earth orbit satellites using onboard GNSS observations is assessed using six months of flight data from the Sentinel- 6A mission. Based on offline processing of dual-constellation pseudorange and carrier phase measurements as well as broadcast ephemerides in a sequential filter with a reduced dynamic force model, navigation solutions with a representative position error of 10 cm (3D RMS) are achieved. The overall performance is largely enabled by the superior quality of the Galileo broadcast ephemerides, which exhibits a two- to three-times smaller signal-in-spacerange error than GPS and allows for geodetic grade GNSS real-time orbit determination without a need for external correction services. Compared to GPS only processing, a roughly two times better navigation accuracy is achieved in a Galileo only or mixed GPS/Galileo processing. On the other hand, GPS tracking offers a useful complement and additional robustness in view of a still incomplete Galileo constellation. Furthermore, it provides improved autonomy of the navigation process through the availability of earth orientation parameters in the new civil navigation message of the L2C signal. Overall, GNSS based onboard orbit determination can now reach a similar performance as the DORIS (Doppler Orbitography and Radiopositioning Integrated by Satellite) navigation system. It lends itself as a viable alternative for future remote sensing missions.
Introduction
Sentinel-6A “Michael Freilich,” also known as Jason Continuity of Service (Jason-CS), is the latest satellite of the European earth observation program (Donlon et al. 2021). The primary payload comprises the Poseidon-4 Ku/C-band altimeter and the advanced microwave radiometer climate quality (AMR-C). Altimeter processing relies on highly accurate knowledge of the orbital position of the spacecraft, specifically its altitude, to determine the mean height of the sea level. Sentinel- 6A precise orbit determination (POD) is supported by two independent sensors, namely a Doppler Orbitography and Radiopositioning Integrated by Satellite (DORIS) receiver (Auriol and Tourain 2010) and a “PODRIX” dual constellation global navigation satellite system (GNSS) receiver. For utmost accuracy, data from these instruments are processed on the ground in non-time critical (NTC) or short-time critical (STC) processes. In addition, the DORIS Immediate Orbit DEtermination (DIODE; Jayles et al. 2010) system provides onboard navigation solutions with roughly 10 cm (3D RMS) position accuracy and 2–3 cm height accuracy based on real-time processing of Doppler measurements from a network of globally distributed ground beacons. External calibration and validation of orbit products are supported by a laser retroreflector for satellite laser ranging (SLR).
The PODRIX receiver likewise provides a real-time onboard navigation solution, which is mainly intended for platform support rather than science data processing and confined to an accuracy of roughly 3 m. The achieved performance reflects a trade off between performance, algorithmic complexity, and robustness and reflects typical accuracy needs for attitude and orbit control systems of LEO satellites.
It is largely determined by the use of GNSS broadcast ephemerides and basic dynamical models for Kalman filtering, as well as the sole use of GNSS pseudorange measurements. Notably higher accuracy can, in principle, be achieved by processing GNSS carrier phase observations as shown in past research and flight demonstrations of GNSS-based real-time orbit determination for satellites in low earth orbit (LEO). Montenbruck and Ramos-Bosch (2008) presented a reduced dynamics navigation filter for LEO satellites and achieved accuracies of 0.5–0.7 m 3D RMS based on playblack processing of actual dual-frequency GPS observations from five LEO missions in the 400–800 km altitude range. Onboard the PROBA-2 spacecraft, a 1.1 m 3D RMS accuracy was demonstrated with the eXtended Navigation System (XNS) of the Phoenix single-frequency GPS receiver, which could further be improved to 0.7 m in a reprocessing on ground with optimized filter settings (Montenbruck et al. 2012). More recently, Wang et al. (2015), Gong et al. (2019), and Gong et al. (2020) assessed the performance of similar real-time navigation algorithms through offline processing of GPS or GPS/BeiDou-2 measurements from various spacecraft of the USA, Europe, and China. Here 3D position errors of 0.4–0.7 m were obtained based on single- and dualfrequency observations, respectively.
In all of the above analyses, the achievable accuracy of GNSS-based real-time navigation is ultimately limited by the accuracy of GNSS broadcast ephemerides. For GPS, signal-in-space range errors (SISRE) have gradually decreased from roughly 1 m to 0.5 m over the past decade, which contributes to the continued improvement seen over time in the aforementioned studies. Even though the use of process noise in the carrier phase ambiguity states of the navigation filter (Montenbruck and Ramos-Bosch 2008; Wang et al. 2015) can, to a notable extent, reduce the impact of slowly varying GPS orbit and clock offset errors, a 1-dm LEO navigation accuracy appears out of reach today when relying only on GPS navigation data without augmentation. The use of real-time correction data has therefore been suggested by multiple authors (Reichert et al. 2002; Toral et al. 2006; Hauschild 2016; Giordano et al. 2017; Kim and Kim 2018; Murata et al. 2020), but the practical application of this concept is hampered by the limited availability of suitable modems or GNSS receivers for acquiring such correction data on LEO platforms.
With the ongoing build-up of the Galileo constellation, prospects for GNSS-based onboard navigation of LEO satellites have greatly improved in view of its remarkably accurate broadcast ephemerides. At SISRE values of 0.1–0.2 m (Montenbruck et al. 2018), Galileo clearly outperforms GPS and other GNSSs and reduces the contribution of broadcast ephemeris errors in the observation model to less than a wavelength. Carrier-phase-based positioning techniques, which have previously been limited to use with precise ephemerides or augmentation services, can now successfully be applied with orbit and clock data from the standard navigation messages (Carlin et al. 2021). These advantages are likewise of interest for GNSS-based onboard navigation of LEO satellites, which largely relies on the use of un-augmented broadcast ephemerides. Notable benefits of Galileo for this application have been earlier predicted in a simulation study of Hauschild and Montenbruck (2021) but lack a practical confirmation so far. Using actual flight data from the Sentinel-6A satellite now allows to reliably demonstrate the feasibility of 1 dm (3D RMS) real-time navigation using joint GPS and Galileo observations and shows that GNSS offers a viable alternative to DORIS for real-time orbit determination of LEO satellites.
Following a presentation of the GNSS data collected by the PODRIX receiver onboard of Sentinel-6A and relevant auxiliary data, we discuss the real-time navigation algorithms and model tradeoff for the present study. Thereafter, real-time navigation results obtained in post processing from half a year of flight data are presented and the achieved performance is assessed. Furthermore, results are compared against actual realtime navigation results from the DORIS/ DIODE system onboard Sentinel-6A and comparable performance of GPS/ Galileo-based navigation is demonstrated.
Data
The present study covers a six month period from mid December 2020 to mid June 2021 after initial orbit acquisition of the Sentinel-6A spacecraft. It is based on GNSS observations of the PODRIX GNSS receiver and measured attitude information provided as part of the platform and science telemetry. Complementary spacecraft related information includes the mass and GNSS antenna phase center offset from the center-of-mass, as well as information on the time, duration, and planned velocity increment of orbit keeping maneuvers conducted on four days (Feb. 18, Apr. 27/29/30) within the analysis period. Even though the telemetry interface of the PODRIX receiver allows for transmission of a comprehensive set of GPS LNAV and CNAV (ISGPS- 200 2021) as well Galileo INAV and FNAV (EU 2021) broadcast ephemeris parameters, not all of the respective PODRIX output messages are enabled on the Sentinel-6A satellite. To overcome this limitation, which mainly affects the availability of group delays and earth orientation parameters (EOPs), broadcast ephemeris data collected by a global receiver network and made available in the draft RINEX 4 navigation data format (Romero 2021) are used instead for the present study. Other than its predecessors, RINEX 4 provides full support of modernized navigation messages such as the CNAV message of the GPS L2C and L5 signal as well as system time offsets, ionosphere data, and EOPs.
While the ground collected navigation data cover all data transmitted by all GNSS satellites on a day of interest, they are fully representative of the GPS/Galileo orbit, clock offset, group delay, and EOP data available onboard for those GNSS satellites actually tracked by the PODRIX receiver. As such, they provide a legitimate substitute for missing telemetry data in our playback real-time navigation filter.
Concerning observations, the PODRIX receiver does not, by itself, provide a full set of pseudorange and carrier phase observations but rather outputs the code phase, i.e., the transmit time of the ranging signal and the phase of the numerically controlled oscillator that compensates the nominal intermediate frequency and Doppler shift of the down converted signal. Based on these data, conventional pseudorange and carrier phase observations can be formed with knowledge of the receiver time at the instant of the measurement (Won and Pany 2017). For the present work, a receiver time scale aligned to roughly 10 ns with the GPS time scale based on the receiver internal navigation solution is used. The resulting observations are stored on a daily basis in RINEX observation files with 10 s sampling for the subsequent processing.
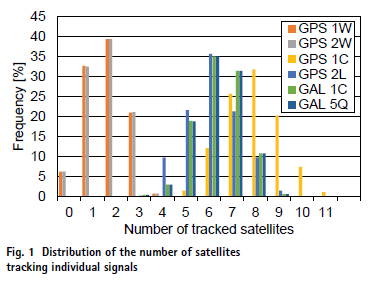
In the default configuration used on Sentinel-6A, the PODRIX receiver uses a semi codeless tracking of the P(Y) signal on the L1 and L2 frequency for GPS Block IIR satellites, while the civil L2C signals are tracked for IIR-M, IIF, and GPS III satellites. In addition, the L1 C/A code signal is tracked for all GPS satellites. For Galileo satellites, the E1 Open Service pilot signal and the E5a pilot signal are tracked. The respective observations and tracking modes are identified by their RINEX identifiers (1W/2W, 1C/2L, 1C/5Q) within this work. In the period of interest, daily averages of 1.8 GPS IIR satellites, 6.0 GPS IIR-M/ IIF/III satellites, and 6.3 Galileo satellites were typically tracked at the adopted 10° elevation mask (Fig. 1). For completeness, it is noted that the two Galileo satellites in eccentric orbits (identified as E14 and E18) are not tracked by the PODRIX receiver on Sentinel-6A, since they are not included in the Galileo almanac. Root-mean-square (RMS) pseudorange errors of the ionospherefree dual-frequency combinations amount to roughly 0.5–0.7 m for GPS 1W/2W and 1C/2L observations and 0.3–0.4 m for Galileo 1C/5Q.
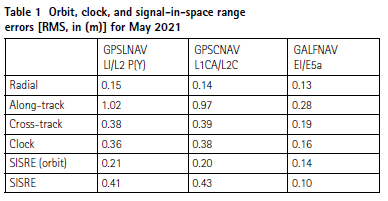
For illustrating the quality of the broadcast ephemeris data, the orbit, clock, and signal-in-space range errors (Montenbruck et al. 2018) for dualfrequency processing are summarized in Table 1 for a sample month in the data analysis period. In case of GPS, separate values are provided for the use of LNAV messages with legacy P(Y) signals as well as CNAV messages with the civil L1 C/A and L2C signals. Differences between the two cases relate to the use of different Keplerian orbit models for fitting the predicted ephemeris as well as the quality of group delay parameters for mapping the clock offset parameters to the observed signals when using the civil L1 C/A and L2C signals. Compared to GPS with roughly daily ephemeris uploads, Galileo benefits primarily from an ephemeris refresh rate of mostly 10 – 30 min and achieves an up to four times smaller SISRE of down to 10 cm.
Algorithms and models
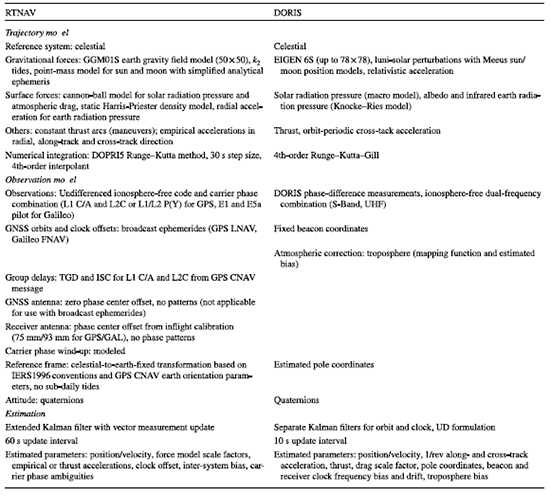
The “RTNAV” navigation filter software used for the processing of Sentinel- 6A GNSS data is described in this section with focus on dynamical and observations models as well as parameter adjustment. The algorithms build on previous work reported in Montenbruck and Ramos-Bosch (2008) but differ in selected aspects such as the choice of the reference system and specific force model contributions, as well as the multi-signal, multi-GNSS extension. While the actual data processing for the present study was performed on a desktop computer in a simulated real-time mode, the core algorithms have earlier been demonstrated in flight (Montenbruck et al. 2012) and are thus considered compatible with the limited resources of representative onboard computers. A summary of various processing models is given in Table 2, which also lists the corresponding counterpart of the DIODE real-time navigation software for onboard processing of DORIS observations (Auriol and Tourain 2010; Jayles et al. 2016).
Table 2 Processing models for Sentinel-6A real-time orbit determination
Trajectory model
The algorithm builds on a reduceddynamic (Yunck et al. 1994) trajectory model for propagating the satellite orbit between consecutive measurement updates in an extended Kalman filter. Here, an a priori set of physical models for the spacecraft motion is complemented by empirical accelerations that are adjusted in the filter to compensate potential deficiencies of the a priori model. While gravitational forces can be modeled with good confidence, limitations typically apply for non-gravitational forces that would require detailed knowledge of the spacecraft structure and surface parameters. For Sentinel- 6A, which orbits the earth at an altitude of roughly 1340 km, a 50 × 50 subset of the GGM01S gravity model (Tapley et al. (2004b)) is adopted and tidal variations are approximated by a basic k2 solid earth tide model (Rizos and Stolz 1985). For an efficient and numerically stable evaluation of the acceleration from the geopotential coefficients, the formulation of Cunningham (1970) is used. Luni-solar perturbations are described through a point-mass model using approximate analytical models of the sun and moon position with representative accuracies of 1 to 5 arcminutes (Montenbruck and Gill 2000).
Drag, which has an almost negligible impact at the orbital height of Sentinel- 6A, is described through a cannon-ball model with a static Harries and Priester (1962) density model and an adjustable scale factor ( CD). For solar radiation pressure (SRP), a cannon-ball model with an adjustable scale factor ( CR ) is applied along with a cylindrical shadow model. Earth-radiation pressure (ERP) is approximated by a constant radial acceleration with a value of 30 nm/s2 that represents the average acceleration obtained from more detailed ERP models for the Sentinel-6A spacecraft and orbit (Montenbruck et al. 2021). Finally, piecewise constant accelerations in radial (R), along-track (T), and cross-track (N) direction can be applied to describe empirical accelerations or thrust arcs during orbit control maneuvers. Such maneuvers are modeled using a priori information on the start time, duration, and approximate velocity increment in the three axes. Within the Kalman filer, additional process noise in the position and velocity states is used to compensate errors in the a priori maneuver modeling.
The equation of motion is formulated as a first-order differential equation
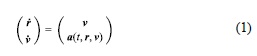
for the position r and velocity v as a function of the time t and the acceleration a . Contrary to Montenbruck and Ramos- Bosch (2008), who proposed an earthfixed formulation of the equation of motion to minimize the need for reference system transformations, an inertial formulation is adopted in the present work. It implies the need for explicit transformations between the celestial and terrestrial reference systems in the observation model and on the output of the estimated state vector. Despite a higher computational effort, the inertial formulation is preferred here to avoid the impact of small simplifications in the modeling of Coriolis forces in the earthfixed approach. These simplifications were found to require larger empirical accelerations, particularly in the crosstrack direction, and ultimately limit the achievable orbit determination accuracy.
Next to the equation of motion, a simplified set of variational equations is used to establish the state-transition matrix and the position/velocity partials with respect to SRP and drag scale factors as well as the RTN accelerations. The six-stage, fifth-order Runge–Kutta method of Dormand and Prince (1980) is used for numerical integration of the equation of motion and the variational equations with a fixed step-size of 30 s. The method can be favorably combined with a fourth-order interpolant (Hairer et al. 1987) to support dense output. This allows the generation of trajectory information at, e.g., 1 s or 10 s, without limiting the actual integrator step size.
Observation model
In accord with the capabilities of the PODRIX receiver on Sentinel- 6A, the RTNAV filter is designed to support GNSS observations of satellitespecific signals and from multiple constellations. The ionosphere-free pseudorange (p) and carrier-phase (φ) observations are thus described by the generic observation model
![]()
where |rk – r| denotes the distance between the position rk of a tracked satellite k of constellation ck at signal transmission and the receiver r at signal reception. dtkdenotes the satellite clock offset relative to the constellation-specific system time as provided in the broadcast navigation message. Analogously, dtrcv denotes the receiver clock offset. It is referred to a selected reference constellation, here GPS, and the corresponding reference signal of the broadcast clock offsets, i.e., the ionosphere-free combination of L1 and L2 P(Y)-code observations. The inter-system bias, or ISB, dtck is conventionally set to zero for the reference constellation. For satellites of other constellations, it combines the system time difference, here the Galileo- GPS time offset (GGTO), and receiver and constellation-specific biases between the tracked signals and the reference signals. Despite an a priori calibration of receiver biases in the PODRIX receiver data, residual biases cannot be neglected in practice and must be adjusted in the orbit and clock determination. As such, they can readily be lumped with the GGTO and no need arises to explicitly use the GGTO value provided in the Galileo navigation message.
For pseudorange measurements, the observation model furthermore accounts for a satellite code bias contribution Bk,sk ,sref,k, which depends on the satellite k, the tracked set of signals sk and the set of broadcast clock reference signals sref,k for the specific constellation. In the present application, the bias vanishes for GPS P(Y) tracking as well as Galileo E1/ E5a tracking in combination with the use of FNAV ephemerides. For GPS L1 C/A and L2C tracking in contrast, the bias does not vanish and needs to be applied in the model. It is formed from the timing group delay parameter, TGD, and the ISCL2C inter-signal correction as detailed in ISGPS- 200 or Montenbruck and Hauschild (2013). For carrier-phase observations, an ambiguity term Ak is included in the observation model. It is adjusted from the observations and lumps any remaining carrier phase biases that are not explicitly considered in the model. Furthermore, it is used to absorb errors on the modeled carrier phase caused by broadcast orbit and clock errors by allowing for process noise in the estimation of these parameters. Following Wu et al. (1993), the carrier phase model also considers the contribution of phase wind-up Ψ based on the time-varying orientation of the transmit and receive antennas.
The observation model is evaluated with satellite and receiver positions in an earth-fixed reference frame that aligns with the reference frame of the broadcast ephemerides. While GPS and Galileo make use of constellation-specific realizations of the international terrestrial reference system, namely WGS84 and GTRF, differences with respect to each other and the most recent version of the international reference frame, ITRF2014, are at the centimeter level (NGA 2021; Enderle 2018; Malys et al. 2021) and have been neglected in the present context. Following the numerical integration of the equation of motion, the spacecraft position needs to be transformed from the celestial to the terrestrial frame to obtain the ITRF position of the receiver antenna as required by the observation model. The IERS 1996 models (McCarthy 1996) of precession, nutation, and earth rotation are adopted for this purpose in view of a reduced complexity compared to the more rigorous IERS 2010 conventions (Petit and Luzum 2010). For improved efficiency, trigonometric functions in the nutation model are recursively computed using addition theorems. Pole coordinates xp and yp as well as the UT1-UTC difference required in the transformation at the epoch of interest are obtained from predictions of these values transmitted in the form of linear polynomial approximations within the CNAV navigation message of the GPS L2C signal and updated once per day by the ground segment.
For completeness, we note that the observation model ties the estimated spacecraft position to the earth fixed frame that is implied by the broadcast ephemerides of the tracked GNSS satellites. Uncertainties or approximations in the celestial-to-terrestrial transformation mainly affect the realization of the inertial system used for the trajectory propagation, which may thus deviate slightly from the International Celestial Reference System (ICRF). However, the transformation from this approximate celestial system using the approximate ICRF-to-ITRF transformation correctly replicates the observed motion in the WGS84/GTRF frame. As such, only the earth fixed position and velocity output by the navigation filter will be used for comparison with reference orbit products to assess the achievable real-time navigation accuracy.
Estimation
An extended Kalman filter is used to adjust the position, velocity and receiver clock at the time of the measurement. Overall, the filter state
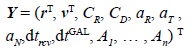
comprises the inertial position and velocity of the spacecraft center-ofmass, the SRP and drag scale factors ( CR, CD ), empirical accelerations or thrust accelerations (aR, aT , aN) in radial, alongtrack and cross-track direction, the GPS-referenced receiver clock offset, the ISB for Galileo, and a carrier phase ambiguity for each of the tracked satellites.
In the time update step of the filter, position and velocity are propagated through numerical integration, while the force model scale factors, clock parameters, and ambiguities are predicted with a unit state transition matrix. Empirical accelerations are treated as exponentially correlated random variables (Tapley et al. 2004a). They are kept constant during the numerical trajectory propagation from the last epoch ti−1 to the new measurement epoch ti = ti−1 +Δt , but their predicted value at that epoch is obtained by scaling with an exponential damping factor m = eΔt∕τ using a predefined correlation time τ with a representative value of 600 s. White process noise with variance q proportional to the measurement interval is applied to the SRP and drag scale factors as well as the clock and ISB states, while the process noise variance
![]()
of the empirical accelerations depends on the selected steady state variance σa and the exponential mapping factor.
GNSS carrier phase ambiguities are conceptually constant values and no process noise would normally be applied in their estimation. However, as previously discussed in Montenbruck and Ramos-Bosch (2008) and Wang et al. (2015), process noise in the ambiguity states provides a convenient means to compensate the impact of signal-in-space range errors when working with broadcast ephemerides. Instead of adjusting a dedicated SISRE parameter for each tracked satellite that adds to both the modeled pseudorange and carrier phase (Gunning et al. 2019), gradually varying ephemeris errors can likewise be absorbed in a lumped state reflecting the sum of the ambiguity and SISRE parameter. While this approach ignores the SISRE contribution in the pseudorange, this simplification is generally acceptable in practice in view of the lower pseudorange weight and the comparatively short arcs of continuous carrier phase tracking for receivers onboard a LEO satellite. The amount of process noise applied in the ambiguity states is motivated by the constel-lation-specific variation in GNSS clock offsets errors and line-of-sight orbit errors. Process noise values minimizing the overall errors of the estimated trajectory can best be obtained with the filter tuning using a parametric search and a precise reference trajectory for the desired mission. In the present work, representative process noise variances of qA = (40 mm)2and qA = (14 mm)2were applied at measurement intervals of 60 s.
Results and discussion
Based on the algorithms and input data described above, GNSS navigation filter results for Sentinel-6A were computed in a simulated real-time mode. As a reference for the performance assessment and initial filter tuning, precise orbit determination results based on ambiguityfixed processing of GPS and Galileo observations from the PODRIX receiver were used (Montenbruck et al. 2021). These reference orbits were independently verified through satellite laser ranging and show sub centimeter RMS residuals after consideration of station specific biases. Furthermore, they exhibit consistency better than 1 cm 3D RMS compared with the combined, multi agency solution generated as part of the Copernicus POD service (CPOD 2021).
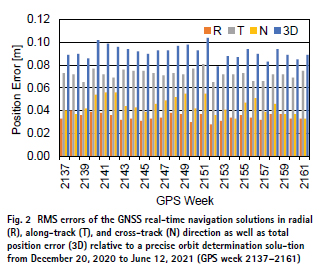
Weekly solutions exhibit a stable performance with position errors of about 10 cm (Fig. 2). In each of these solutions, a 15-min interval at the beginning of the data arc has been excluded from the comparison to mask the early convergence phase of the navigation filter. The overall error budget is dominated by the alongtrack component, which is only weakly constrained by the dynamical models and exhibits errors of 6–8 cm RMS. Errors in the radial component, which are of primary relevance for altimetry, range from 3–4 cm RMS, while crosstrack errors amount to 4–6 cm RMS. The combined error perpendicular to the flight direction is well within common requirements for the generation of synthetic aperture radar (SAR) images (Roselló Guasch 2010; Breit et al. 2010), and a GNSS-based onboard navigation solution could thus facilitate quick look processing of SAR.
RMS velocity errors of the weekly solutions relative to the precise reference amount to 0.08–0.10 mm/s in the period of interest, and the along-track components of the velocity error are confined to 0.03–0.04 mm/s RMS. This falls well within the needs for (near-) real-time orbit determination of common radio occultation missions, which require a 0.05–0.20 mm/s along-track velocity accuracy to retrieve bending angle profiles from the observed Doppler excess (Kursinski et al. 1997, Roselló Guasch 2010). It must be noted, though, that the achievable accuracy of the velocity component depends largely on the quality of the a priori force model and clearly benefits from the comparatively high altitude of the Sentinel-6A mission. Spacecraft operated at lower altitudes and experiencing higher drag forces would typically require an increased level of empirical forces, which then reduces the dynamical constraints on the resulting orbit. Nevertheless, independent simulations of GNSS-based real-time navigation (Hauschild and Montenbruck 2021) suggest that a better than 0.1 mm/s along-track velocity accuracy can even be reached for spacecraft orbiting at down to 400 km altitude.
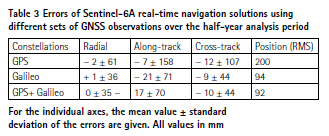
The achieved accuracy is clearly dominated by the contribution of Galileo, which offers both lower measurement noise and reduced broadcast ephemeris errors when compared to GPS. As shown in Table 3, a Galileo only processing can in fact provide an almost identical performance as the combined solution, while the stand-alone GPS solution shows roughly two times larger errors in all components. Given the reduced number of Galileo satellites available in the current mission phase and available for tracking by the PODRIX receiver, smaller errors may, however, be obtained on average in the start up phase of the navigation filter when jointly processing both constellations. Also, it must be emphasized that Galileo does not offer earth orientation parameters as part of its navigation messages and a regular EOP upload from the ground would therefore be required for LEO satellites using a Galileo only real-time navigation system.
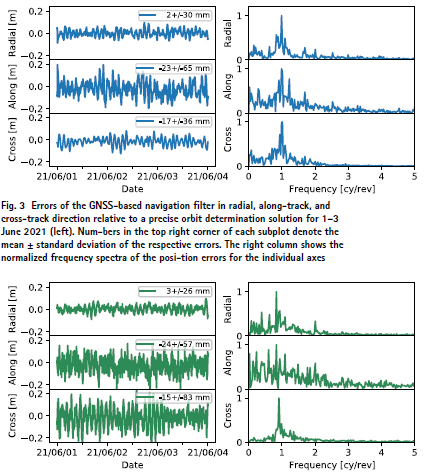
Fig. 4 Errors of the DORIS real-time navigation solution
in radial, along-track, and cross-track direction relative
to a precise orbit determina- tion solution for 1–3 June 2021 (left). Numbers in the top right corner of each subplot denote the mean ± standard deviation of the respective errors. The right column shows the normalized frequency spectra of the posi- tion errors for the individual axes
As recognized from Table 3, the solutions of the GNSS navigation filter exhibit small but discernible mean off- sets in the along-track and cross-track direction. In the latter case, the bias can, at least partly, be understood by an apparent inconsistency of about 7 mm in the center- of-mass offset of the GPS antenna provided by the manufacturer, which has previously been discussed in Montenbruck et al. (2021). While carrier phase ambiguity fixing aligns the precise orbit determination solution in such a way as to reflect the observed motion of the antenna properly, a float ambiguity processing tends to reflect the actual motion of the center of mass due to the dynamical constraints in orbit-normal direction. Based on the analysis of satellite laser ranging measurements, a 7-mm cross-track bias has been identified in the POD solutions used as a reference for the present study, which can thus explain the dominant part of the mean cross- track bias of the GNSS real-time solutions. No indication of systematic offsets in the reference orbit exists for the along-track direction, and the biases in Table 3 must solely be attributed to the real-time navigation filter. Tests with different filter parameters show that the magnitude of the along-track bias depends on the amount of process noise applied in the ambiguity states and can be decreased at the expense of a higher overall position error. A mapping of along-track position errors into gradual variations in the carrier-phase ambiguities is therefore suspected as an explanation for the observed biases. However, given the magnitude of the along-track bias and its limited relevance in common applications of (near-)real-time orbit products, it appears well tolerable in practice.
As a final step of the performance characterization, we compare the solution of the GNSS navigation filter with the actual flight results of the DORIS/DIODE system on Sentinel-6A. The variation in position errors for a common 3-day interval is shown in Figs. 3 and 4 for the two techniques. In both cases, precise orbit determination results based on ambiguityfixed GPS/Galileo observations from Montenbruck et al. (2021) were used as a reference for the performance analysis. Overall, both systems show an almost identical performance in radial and alongtrack direction, but a slightly different short-term behavior may be recognized for the latter. While the present results show a dominant once-per-revolution variation in the along-track-position error, the DIODE solution exhibits a slightly higher scatter on sub-orbital time scales. These differences indicate a higher reliance of the present GNSS navigation filter on the dynamical model for the current tuning, while the DIODE results are slightly more kinematic in nature and show a stronger influence of measurement noise. As the most obvious difference, larger errors in cross-track direction can be observed for the DIODE solution. These occur at a frequency of 0.92 cycles per orbital revolution, which differs from the orbital frequency (1 cy/rev) by the mean rate of earth rotation. Aside from a weaker geometric strength of the DORIS observations in cross-track direction, the performance difference may in part be attributed to differences in the empirical acceleration model. While DIODE applies a harmonic, once-per-revolution model, the cross-track acceleration is described by an exponentially correlated random variable in the GNSS navigation filter. Presumably, this model can compensate temporal variations in unmodeled accelerations in a better manner. For completeness, it is noted that further model improvements reducing the crosstrack error to roughly 4–5 cm are available in a new DIODE software version, but have not yet been loaded on Sentinel-6A.
Summary and conclusions
The accuracy of GPS broadcast ephemerides has long limited GNSSbased real-time orbit determination of satellites in low earth orbit. These are characterized by signal-in-space range errors of roughly 0.5 m and have enabled 3D RMS positioning errors of the same magnitude in past studies of GPSbased real-time navigation. Notably, the Galileo system provides improved prospects for accurate onboard navigation of LEO satellites, which offers SISRE values of down to 0.1 m. Making use of actual flight data from the Sentinel- 6A satellite, which hosts the first spacegrade GPS/Galileo receiver, we assessed the achievable navigation accuracy with observations of both constellations.
The processing is performed with an extended Kalman filter that builds on a reduced dynamic force model and processes the pseudorange and carrier phase observations purely sequentially. For maximum accuracy, the impact of broadcast ephemeris errors is compensated by including a white noise parameter in the carrier phase observation model. This parameter lumps the actual phase ambiguity with GNSS clock and line-ofsight orbit errors, and ultimately enables a 0.1 m 3D RMS accuracy in the GPS + Galileo processing. A similar performance can, in principle, be achieved in Galileo only processing but requires external earth orientation parameters. These are presently only transmitted by the modernized GPS satellites and would need to be incorporated into the Galileo navigation message to enable fully autonomous Galileo only navigation of LEO satellites.
Overall, the achieved performance closely matches that of the DIODE system for DORIS-based real-time navigation onboard the Sentinel-6A satellite. So far, DIODE represents the only fully operational onboard navigation system that is able to achieve 10-cm real-time navigation for LEO satellites. The results achieved in the present study show that similar performance can now as well be achieved from GNSS observations. Nowadays, GNSS receivers for space applications are widely available, so GNSS-based real-time navigation systems can provide an interesting and complementary alternative to DORIS state-of-the-art accuracy. Applications that can benefit from this development include science missions for altimetry, SAR imaging, or atmospheric profiling, but also satellite formations or mega constellations. In combination with commercial-of-the-shelf GNSS receivers, the technology is of particular interest for low-cost missions and missions with tight engineering budgets.
At a 10-cm 3D RMS position error, the GNSS-based real-time navigation solution is expected to meet even demanding needs for onboard position knowledge, but certainly still lags behind the performance achievable in ground-based POD. In part, this can be attributed to the forward only processing in sequential estimation schemes for realtime processing, which commonly shows a factor of two performance degradation compared to a forward–backward filter smoother or least squares estimator. As shown by the comparison of GPS and Galileo only processing, the broadcast ephemeris quality clearly impacts the achievable navigation performance. Use of real-time correction data could thus contribute to lower SISRE and a homogeneous quality for all tracked GNSSs, but the remarkable quality of Galileo broadcast ephemerides already sets a high standard for the performance of potential correction services. Furthermore, improved GNSS ephemeris data alone may not be sufficient, and further model improvements will likely be required when trying to bridge the performance gap between real-time and ground-based POD processing. This relates both to dynamical models, where improved a priori models for the nongravitational forces would reduce the need for empirical parameters, and measurement model improvements thus as use of phase pattern calibrations. Most notably, single-receiver ambiguity resolution would be expected to enable further improvements in the real-time orbit determination accuracy, but would require dedicated real-time GNSS orbit and clock products with associated code and phase bias information.
Acknowledgements
Sentinel-6A GNSS data used in this study have kindly been made available by EUMETSAT and the European Commission (EC) as part of the Copernicus program. The authors would also like to express their thanks to Centre National D’Etudes Spatiales (CNES) and Collecte Localisation Satellites (CLS) for the provision of DORIS/DIODE real-time navigation solutions, which served as a reference for the performance characterization of the present algorithms. Furthermore, we are grateful to the CNES/CLS DORIS team for valuable discussion on the DIODE system and their contribution to the review of this article.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Open Access
This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http:// creat iveco mmons. org/ licen ses/ by/4. 0/.
References
Auriol A, Tourain C (2010) DORIS system: the new age. Adv Space Res 46(12):1484–1496. https:// doi. org/ 10. 1016/j. asr. 2010. 05. 015
Breit H, Fritz T, Balss U, Lachaise M, Niedermeier A, Vonavka M (2010) TerraSAR-X SAR processing and products. IEEE Trans Geosci Remote Sens 48(2):727–740. https:// doi. org/ 10. 1109/ TGRS. 2009. 20354 97
Carlin L, Hauschild A, Montenbruck O (2021) Precise point positioning with GPS and Galileo broadcast ephemerides. GPS Solut 25(2):77. https:// doi. org/ 10. 1007/ s10291- 021- 01111-4
CPOD (2021) Copernicus POD Regular Service Review Apr.- Jun 2021, Copernicus Sentinel-1, -2, -3 and -6 Precise Orbit Determination Service (CPOD), GMV-CPODRSR- 0021, 2021/06/23
Cunningham LE (1970) On the computation of the spherical harmonic terms needed during the numerical integration of the orbital motion of an artificial satellite. Celest Mech 2(2):207–216. https:// doi. org/ 10. 1007/ BF012 29495
Donlon CJ, Cullen R, Giulicchi L, Vuilleumier P, Francis CR, Kuschnerus M, Simpson W, Bouridah A, Caleno M, Bertoni R et al (2021) The Copernicus Sentinel-6 mission: enhanced continuity of satellite sea level measurements from space. Remote Sens Environ 258:112395. https:// doi. org/ 10. 1016/j. rse. 2021. 112395
Dormand JR, Prince PJ (1980) A family of embedded RungeKutta formulae. J Comput Appl Math 6(1):19–26. https:// doi. org/ 10. 1016/ 0771- 050X(80) 90013-3
Enderle W (2018) Galileo Terrestrial Reference Frame (GTRF)— Status, ICG-13, 4–9 November 2018, Xi’an, China, UNOOSA. https:// www. unoosa. org/ docum ents/ pdf/ icg/ 2018/ icg13/ wgd/ wgd_06. pdf. Accessed 1 Aug 2021
EU (2021) European GNSS (Galileo) Open Service, Signal-in-Space, Interface Control Document, Issue 2.0
Giordano P, Zoccarato P, Otten M, Crisci M (2017) P2OD Realtime precise onboard orbit determination for LEO satellites In: Proceedings of ION GNSS+ 2017, Portland, Oregon, pp 1754–1771. https:// doi. org/ 10. 33012/ 2017. 15190
Gong X, Guo L, Wang F, Zhang W, Sang J, Ge M, Schuh H (2019) Precise onboard real-time orbit determination with a low-cost single-frequency GPS/BDS receiver. Remote Sens 11(11):1391. https:// doi. org/ 10. 3390/ rs111 11391
Gong X, Sang J, Wang F, Li X (2020) LEO onboard real time orbit determination using GPS/BDS data with an optimal stochastic model. Remote Sens 12(20):3458. https:// doi. org/ 10. 3390/ rs122 03458
Gunning K, Blanch J, Walter T (2019) SBAS corrections for PPP integrity with solution separation. In: Proceedings of ION ITM 2019, Reston, VA, USA, January 28–31, pp 707–719. https:// doi. org/ 10. 33012/ 2019. 16739
Hairer E, Norsett SP, Wanner G (1987) Solving ordinary differential equations I. Springer-Verlag, Berlin-Heidelberg-New York
Harris I, Priester W (1962) Timedependent structure of the upper atmosphere. NASA 87-FM-2, Goddard Space Flight Center, MD
Hauschild A, Tegedor J, Montenbruck O, Visser H, Markgraf M (2016) Precise onboard orbit determination for LEO satellites with real-time orbit and clock corrections. In: Proceedings of ION GNSS+ 2016, Portland, Oregon, pp 3715–3723. https:// doi. org/10. 33012/ 2016. 14717
Hauschild A, Montenbruck O (2021) Precise real-time navigation of LEO satellites using GNSS broadcast ephemerides. NAVIGATION J Inst Navig 68(2):419–432. https:// doi. org/ 10. 1002/ navi.416
IS-GPS-200 (2021) NAVSTAR GPS Space Segment/Navigation User Interfaces, IS-GPS-200 Rev. M, 21 May 2021, Space and Missile Systems Center, Los Angeles Air Force Base
Jayles C, Chauveau JP, Rozo F (2010) DORIS/Jason-2: better than 10 cm onboard orbits available for nearreal- time altimetry. Adv Space Res 46(12):1497–1512. https:// doi. org/ 10. 1016/j. asr. 2010. 04. 030
Jayles C, Chauveau JP, Didelot F, Auriol A, Tourain C (2016) DORIS system and integrity survey. Adv Space Res 58(12):2691–2706. https:// doi. org/ 10. 1016/j. asr. 2016. 05. 032
Kim J, Kim M (2018) Orbit determination of low-earth-orbiting satellites using space-based augmentation systems. J Spacecr Rocket 55(5):1300–1302. https:// doi. org/ 10. 2514/1. A34061
Kursinski ER, Hajj GA, Schofield JT, Linfield RP, Hardy KR (1997) Observing Earth’s atmosphere with radio occultation measurements using the Global Positioning System. J Geophys Res 102(D19):23429–23465. https:// doi. org/ 10. 1029/ 97JD0 1569
Malys S, Solomon R, Drotar J, Kawakami T, Johnson T (2021) Compatibility of Terrestrial Reference Frames used in GNSS broadcast messages during an 8 week period of 2019. Adv Space Res 67(2):834–844. https:// doi. org/ 10. 1016/j. asr. 2020. 11. 029
McCarthy DD (1996) IERS Conventions (1996), IERS Technical Note No. 21, US Naval Observatory
Montenbruck O, Gill E (2000) Satellite orbits. Springer Verlag, Heidelberg
Montenbruck O, Hauschild A (2013) Code biases in multi-GNSS point positioning. In: Proceedings of ION ITM 2013, 28–30 Jan. 2013, San Diego, pp 616–628
Montenbruck O, Ramos-Bosch P (2008) Precision real-time navigation of LEO satellites using global positioning system measurements. GPS Solut 12(3):187–198. https:// doi. org/ 10. 1007/s10291- 007- 0080-x
Montenbruck O, Swatschina P, Markgraf M, Santandrea S, Naudet J, Tilmans E (2012) Precision spacecraft navigation using a lowcost GPS receiver. GPS Solut 16(4):519–529. https:// doi.org/ 10. 1007/ s10291- 011- 0252-6
Montenbruck O, Steigenberger P, Hauschild A (2018) Multi- GNSS Signal-in-space range error assessment—methodology and results. Adv Space Res 61(12):3020–3038. https:// doi. org/ 10.1016/j. asr. 2018. 03. 041
Montenbruck O, Hackel S, Wermuth M, Zangerl F (2021) Sentinel-6A precise orbit determination using a combined GPS/Galileo receiver. J Geodesy 95(9):109. https:// doi. org/ 10. 1007/s00190- 021- 01563-z.
Murata M, Kawano I, Inoue K (2020) Precision onboard navigation for LEO satellite based on precise point positioning. In:Proceedings of IEEE/ION position, location and navigation symposium (PLANS), pp 1506–1513. https:// doi. org/ 10. 1109/PLANS 46316. 2020. 91101 58
NGA (2021) Recent update to WGS 84 reference frame and NGA transition to IGS ANTEX, National Geospatial-Intelligence Agency. https:// earth- info. nga. mil/ php/ downl oad. php? file= (U)WGS% 2084(G2139). pdf. Accessed 1 Aug 2021
Petit G, Luzum B (2010) IERS Conventions (2010), IERS Technical Note No. 36. Verlag des Bundesamtes für Kartographie und Geodäsie, Frankfurt am Main
Reichert A, Meehan T, Munson T (2002) Toward decimeter-level real-time orbit determination: a demonstration using the SAC-C and CHAMP spacecraft. In: Proceedings of ION GPS 2002, Portland, Oregon, pp 1996–2003
Rizos C, Stolz A (1985) Force modelling for GPS satellite orbits. In: Proceedinsg of 1st international symposium on precise positioning with GPS, Rockville, MD, vol 87–98
Romero I (ed) (2021) RINEX the receiver independent exchange format version 4.00, 1 Dec 2021 Roselló Guasch J, Silvestrin P, Aguirre M, Massotti L (2010) Navigation needs for ESA’s Earth observation missions. In: Sandau R, Roeser HP, Valenzuela A (eds) Small satellite missions for Earth observation. Springer, Berlin, pp 439–447. https:// doi. org/10. 1007/ 978-3- 642- 03501-2_ 41
Tapley BD, Schutz BE, Born G (2004a) Statistical orbit determination. Elsevier Academic Press. https:// doi. org/ 10. 1016/ B978-0- 12- 683630- 1. X5019-X
Tapley BD, Bettadpur S, Watkins M, Reigber C (2004b) The gravity recovery and climate experiment: mission overview and early results. Geophys Res Lett 31(9):L11501. https:// doi. org/ 10.1029/ 2004G L0197 79
Toral M, Stocklin F, Bar-Server Y, Young L, Rush J (2006) Extremely accurate on-orbit position accuracy using NASA’s tracking and data relay satellite system (TDRSS). In: Proceedings of 24th AIAA international communications on satellite systems conference (ICSST), pp 2006–5312. https:// doi. org/ 10. 2514/6. 2006- 5312
Wang F, Gong X, Sang J, Zhang X (2015) A novel method for precise onboard real-time orbit determination with a standalone GPS receiver. Sensors 15(12):30403–30418. https:// doi. org/ 10. 3390/s1512 29805
Won JH, Pany T (2017) Signal processing. In: Teunissen P, Montenbruck O (eds) Springer handbook of global navigation satellite systems. Springer, pp 401–442
Wu JT, Wu SC, Hajj G, Bertiger WI, Lichten SM (1993) Effects of antenna orientation on GPS carrier phase. Manuscr Geodaet 18(2):91–98
Yunck TP, Bertiger WI, Wu SC, Bar- Sever YE, Christensen EJ, Haines BJ, Lichten SM, Muellerschoen RJ, Vigue Y, Willis P (1994) First assessment of GPS-based reduced dynamic orbit determination on TOPEX/Poseidon. Geophys Res Lett 21(7):541–544. https:// doi. org/ 10. 1029/ 94GL0 0010
The paper is originally publsihed by Springer in GPS Solutions (2022) 26:12. This is republsihed here with authors’ permission. © The Author(s) 2021













 (3 votes, average: 3.33 out of 5)
(3 votes, average: 3.33 out of 5)





Leave your response!