| Positioning | |
On the search algorithm of independent baselines
This paper first introduces six search algorithms of independent baselines and realizes them by program, then the search algorithms are compared with real examples |
 |
|
 |
|
 |
|
Theoretically in the simultaneous observation of the high-precision GPS network solution mode, the selection of the independent baseline vector can be arbitrary with the same adjustment. But in the real situation, the results varies in different selections for the model of baseline solution is imperfect[1]. Solving this problem requires two steps, to determine the weight of the baseline and to search for the independent baseline with the maximum weight[2]. This paper is to describe six ways used in the search algorithm of independent baselines and realizes them by C++ language, by comparing, we know Prim algorithm, Kruskal algorithm[3] and matr ix rank solution[1] are able to get the independent baseline set with maximum weight. Based on the matrix rank solution, the w eight is respectively determined by the length, prec ision and relative precision of the baseline[4], then the adjustment results are analyzed.
Introduction of several Search Algorithms of Independent baseline
Ray method
The ray method is to select a reference point from n points and the independent baselines are the ones from the reference point to the remaining n-1 points. Then the inde pendent baseline set with maximum weight is obtained by comparing n kinds of independent baseline set. This search algorithm is relatively simple to get the independent baseline set with maximum weight with only the weight of ray sets derived from n reference points.
Wire method
The wire method starts from a point and select the baseline with maximum weight connected to it , then starts the other endpoint to search for the baseline with maximum weight until all the n points are connected.
Prim algorithm
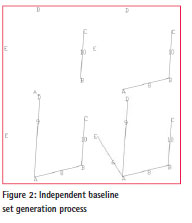
Prim algorithm is to select the side of the minimum weight with one end in the tree while the other is not in the tree and add it to the tree until n-1 sides are in the tree[5]. The realization of the process is shown in Figure 2.
Kruskal algorithm
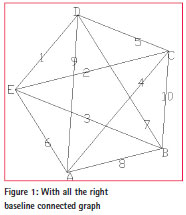
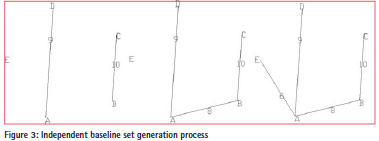
Kruskal algorithm examines each side according to the increasing order of the weight of the side. If the side and the selected ones do not constitute a loop, then reselect the baseline and repeat the process until the spanning tree appears[5]. Take Figure 1 as example, the specific process is represented by Figure 3.
Matrix rank solution
Assume there is a point set Point[n], Vector V[j] represents the directing relationship between any two points, in which j=1/2[n(n-1)]. The overall idea of the matrix rank solution is to maintain a gradually increasing optimal set of independent vectors by continuously updating the correlation matrix until the completion of the search[1].
The following method is used to construct the pth row (p=3, 4, …, n-1) of the correlation matrix:

Calculate the rank of the correlation matrix. If the rank equals to the number of independent baseline set, keep it in the set as the vector V12, if not, it will be removed from the set as V15 for it contributes to a dependent set. Repeat the above steps until the rank of the matrix becomes n-1which means all the n-1 independent vectors have been found and the search of independent vector set is finished.
Programming
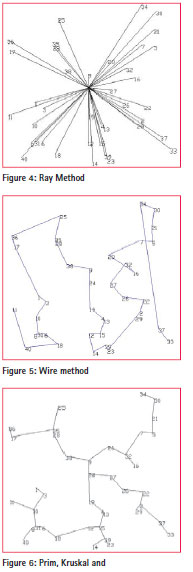
This paper introduces six kinds of algorithms and uses C + + language to program the six kinds of search algorithms, then determine the weight of the simulate GPS control network (40 sites, 780 baseline) by baseline length (the longer, the smaller) to search for the independent baseline set. Figure 4, Figure 5, Figure 6 and Table 1 is the network chart and total length of baseline with six independent baseline search methods.
Examples
Profiles of survey area
The data is the GPS observation data released by the SOPAC. The 36 observation stations lie in an area of 80km at 34W , 116W , and the observation duration is from 189(2011) to 193(2011) with 24 hours every day and data of 12 observation stations is used in each day. As follows:
The 189th day: bmhl, ldes, opbl, opcl, opcp, opcx, oprd, p598, p599, p610, p795, sdhl, total; The 190th day: bemt, bmhl, ctms, ldes, oaes, opcl, p585, p598, p599, sdhl, widc, wwmt; The 191th day: bemt, bmhl, cact, hnps, oaes, opbl, opcp, p504, p511, p607, p608, p610; The 192th day: bemt, cact, cotd, kyvw, p504, p600, p601, p607, psap, thmg, widc, wwmt;
The 193th day: cotd, p490, p491, p504, p600, p741, pin1, pin2, psap, thmg, tmap, wwmt;
Calculating
The O file calculated by GAMIT is the input file. Based on the matrix rank solution, the weight is respectively determined by the length, precision and relative precision of the baseline then search for the independent baseline set in the synchronous loop. Each synchronous loop contains 12 IGS stations and 66 baselines, 11 of which are independent ones, so in the whole 5 time durations 55 independent baselines are included. The following search results are obtained respectively by the above 3 methods of weight determination. Figure 7, Figure 8 and Figure 9 are the control net figures, red line represents the repetitive baseline.
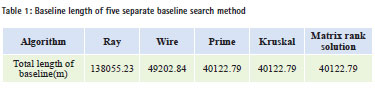
The first weight- determining method concludes 12 repetitive baselines, the second 5, the third 2. The network we get by the first method is simple and the baselines that constitute the net are very short ; the network we get by the second method is relative compact and stable; the network we get by the third method a is complicated and the baselines that constitute the net are relatively long.
Analysis of results
Analysis of external fit precision
Make adjustment of the independent baseline sets processed by the three methods with COSA. Set P504, P511, OPRD and P598 as the known points. Compare the results with the 32 IGS station coordinates published by the SOPAC. As shown in figure 10, figure 11 and figure 12.
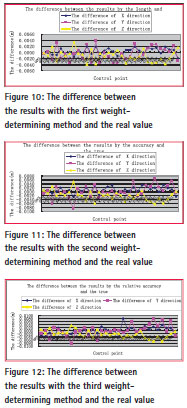
As we can see from figure 10-12, the results from the second weightdetermining method (by precision) are better than others for differences with real value are not obvious, whi ch are less than 2mm in X direction while 4mm in Y and Z direction. The results from the second The results by second weightdetermining method differs from the true value with 6mm in Y and Z direction and some points can reach 8mm, it means that the net obtained by this The results by second weight-determining method is not very stable and there exits jump at some points. The results obtained by the third The results by second weight-determining method (by relative precision) differ from the real value as much as 6mm in Y and Z direction. Analysis of internal fit precision Three control network adjustment results are shown in Figure 13, Figure 14 and Figure 15:

Taking the point precision in all directions as standard, the results of the second weight-determining method (by precision) are better than the other two.
Summaries
This chapter first introduces six search algorithms of independent baseline in detail, namely the Ray method, the Wire method, the Prim method, the Kruskal method and the matrix rank solution, then the weight is determined by length of baseline for the following program, finally we get the conclusion that the Prim, Kruskal and the Matrix rank solution can get a independent baseline set with maximum weight. By analyzing the external and internal fit precision of three methods, we can get the following conclusions: (1) Results from the three methods vary marginally, al l at the level of mm; (2) In the real situation, the results varies in different selections for the model of baseline solution is imperfect. By analyzing the external and internal fit precision of the adjustment results, the second weight-determining method (by precision) can get a relatively better independent baseline set.
Acknowledgments
This research was funded by National Natural Science Foundation of China (No. 41374012) and the 2012 undergraduate comprehensive reform and teaching research project of School of Geodesy and Geomatics, Wuhan university (201220).
References
[1] WANG Lei, LI Pan, LV Cuixian. Application of Vertex Incidence Matrix AIgorithm to Independent Baselines Search and Independent Double- Difference Ambiguity Selection[J]. Geomatics and Information Science of Wuhan University. Jun.2010,35(6):715-718;
[2] Shi Chuang. Adjustment process, analysis theory and application of GPS network in large scale and high precision[M]. Wuhan technical university of surveying and mapping.1999.
[3] Li xianyu.Research Minimum Spanning Tree Based on Prim Algorithm[J]. Computer CD Software and Applications,2010(3):94-95;
[4] Shi Chuang. On the research of process, model and software of high-precision GPS data of national GPS network[D]. Wuhan technical university of surveying and mapping.1995.
[5] Yang Zhiming. Contrasts between Prim and Dijkstra[J]. Journal of Baoshan Teachers’College. Sept.2009,28(5):73-75;













 (4 votes, average: 3.25 out of 5)
(4 votes, average: 3.25 out of 5)





Leave your response!