| Navigation | |
On geodesic based trajectories in navigation
The paper presents the current and uniform approaches to sailing calculations highlighting recent developments. Here we publish the first part of the paper. The concluding part would be published in June 11 issue |
|
 |
|
|||||
 |
|
|||||
The geometry of approximating structures implies the calculus essentially, in particular the mathematical formulae in the algorithms applied in the navigational electronic devices and systems. Thus, we place special emphasis on the geometrical base of the subject. The question we ask affects the range and point in applying the loxodrome (rhumb line) in case the ECDIS equipped with the great circle (great ellipse) approximation algorithms of given accuracy replaces the traditional nautical charts based on Mercator projection. We also cover the subject on approximating models for navigational purposes. Moreover, the navigation based on geodesic lines and connected software of the ship’s devices (electronic chart, positioning and steering systems) gives a strong argument to research and use geodesic-based methods for calculations instead of the loxodromic trajectories in general.
A common problem is finding the shortest connection across the Earth surface between two positions. Such trajectory is always a part of a geodesic (great circle, great ellipse) on the modelling globe surface. The geodesic is used by ship navigators attempting to minimize distances and the radio operators with directional antennae used to look for a bearing yielding the strongest signal. The spherical model is often used in cartographic projections creating the frame of the presented chart. The trajectory of the geodesic lines and the loxodrome looks different depending on the method of the projections given by the strict formulae. Thus, many map projections are invaluable in specialized applications. A Mercator projection is not the only one used by navigators, as the loxodrome does not usually coincides with the geodesic. More commonly applied to large-scale maps, the transverse aspect preserves every property of Mercator’s projection, but since meridians are not straight lines, it is better suited for topography than navigation. Equatorial, transverse and oblique maps offer the same distortion pattern.
THEORETICAL BASE
For curved or more complicated modelling surfaces the metric can be used to compute the distance between two points by integration. The distance generally means the shortest distance between two points. Roughly speaking, the distance between two points is the length of the path connecting them. Most often the research and calculus in navigational literature are considered on the spherical or spheroidal models of Earth because of practical reasons. The flow of geodesics on the ellipsoid of revolution (spheroid) differs from the geodesics on the sphere. There are known different geodesics on the same surface with the same metric considered. However geodesic refers to the metric what is usually not taken into consideration in the navigational lectures. And there are different flows of geodesics on the same surface when different metrics are applied. That means we can obtain geometrically different results in navigational aspect if we change the researched modelling object including its geometrical and physical features [Kopacz, 2006].
Let us focus on two essential notions creating the base for the various fields of the mathematical research: the metric and topology. A metric space is a set with a global distance function (the metric) that, for every two points in, gives the distance between them as a nonnegative real number.
Figure 1. Geometrical basis in geodesic analysis [Kopacz, 2006]
Making one step further we can generalize the metric space to the topological space.
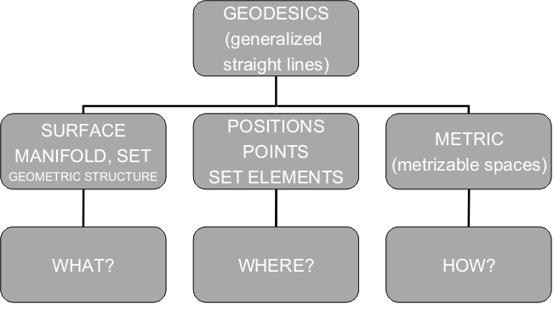
Figure 2. Flows of geodesics (distance functions) on locally modelling surfaces of differing curvatures
The mathematical formulae used in approximation of the navigational calculations are being studied and are based on spherical (spheroidal) model. However if we consider different shape of the surface the formulae change considerably. The examples of the flows of geodesics on locally modelling surfaces of differing curvature are presented graphically in Fig. 2.
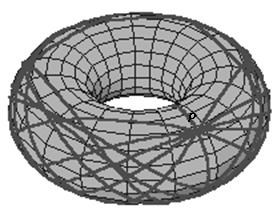
Let us imagine that the vessels do not sail on spheroidal earth but locally torus – shaped planet. In this case the flow of geodesics (Fig. 3) and mentioned rhumb line or used charts are based on other mathematical expressions due to different geometrical object considered. The torus is topologically more simple than the sphere, yet geometrically it is a very complicated manifold indeed. The round torus metric is most easily constructed via its embedding in a Euclidean space of one higher dimension.
Figure 3. The geodesics on a torus T2= S1 x S1 coming from an initial position P
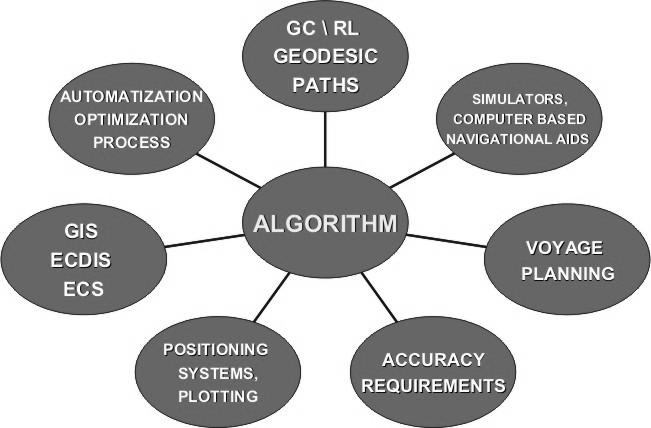
Taking into consideration the main theoretical aspects of the subject above mentioned as well as the practical ones influencing the base and components of the navigational algorithm to be applied we collect all of them together what has been shown in Fig. 4.
Figure 4. Navigational calculations’ algorithm guidelines
The notion of geodesics makes sense not only for surfaces in R3 but also for abstract surfaces and more generally (Riemannian) manifolds. We also refer to [Funar, Gadgil, 2001] where the notion of a topological geodesic in a 3-manifold have been introduced. Geodesics in Riemannian manifolds with metrics of negative sectional curvature play an essential role in geometry. It is shown there that, in the case of 3-dimensional manifolds, many crucial properties of geodesics follow from a purely topological characterization in terms of knotting as well as proved basic existence and uniqueness results for topological geodesics under suitable hypotheses on the fundamental group. For further reading we send the reader to the wide literature on Riemannian and Finsler geometry and topology, in particular the geodesic research.
PLANE MODEL
The surface of revolution as the Earth’s model – sphere S2 or the spheroid is locally approximated by the Euclidean plane tangent in a given position. Generally, we approximate locally the curved surface by the Euclidean plane. For some applications such approximation is allowed and sufficient for practical need of research. That is satisfactory if we do not exceed the required accuracy of provided calculations. Hence the boundary conditions of applying the Euclidean plane or spherical geometry ought to be strictly defined. The mathematical components of the plane Euclidean geometry applied in navigational device are widely known and there is a common Euclidean metric used in the calculus as the distance function. We emphasize that the geodesics may look different even on the plane if different metrics are considered. For the practical reasons and the ease of use there is Euclidean plane tangent to the modelled surface used in many applications, for instance in dynamic positioning (DP) software. The plane model enables the satisfactory accuracy in a local approximation. In the local terrain geodesic research the area can be considered flat if it is inside the circle of a radius of ca. 15.5 km. This corresponds to the area of spherical circle which diameter equals ca. 17’ of the great circle [Kopacz, 2010]. Practically such an approximation allows the direct geodesic measurements without considering the curvature of the modelled Earth surface and presenting the results on the plane in the appropriate scale. In the global modelling of the Earth’s surface (geodesy, cartography, navigation, astronomy) the Euclidean geometry becomes not sufficient for the geometric description and the calculus coming from it. Thus, the limits of application of the approximation methods based on the flat Euclidean geometry must be clearly determined [Kopacz, 2010].
SPHERICAL AND SPHEROIDAL MODEL
As the Earth’s global model an oblate spheroid is used providing the navigational calculations i.e. distances and angles or the sphere for the ease of use. A sphere, spheroid or a torus surface are examples of 2-dimensional manifolds. Manifolds are important objects in mathematics and physics because they allow more complicated structures to be expressed and understood in terms of the relatively well understood properties of simpler spaces. The study of manifolds combines many important areas of mathematics: it generalizes concepts such as curves and surfaces as well as ideas from linear algebra and topology. To measure distances and angles on manifolds, the manifold must be Riemannian. We recall that a Riemannian manifold is an analytic manifold in which each tangent space is equipped with an inner product in a manner which varies smoothly from point to point. This allows one to define various notions such as length, angles, areas (or volumes), curvature, gradients of functions and divergence of vector fields. More general geometric structure a Finsler manifold allows the definition of distance, but not of angle. It is an analytic manifold in which each tangent space is equipped with a norm, in a manner which varies smoothly from point to point. This norm can be extended to a metric, defining the length of a curve; but it cannot in general be used to define an inner product. Any Riemannian manifold is a Finsler manifold. Manifold theory has come to focus exclusively on these intrinsic properties (or invariants), while largely ignoring the extrinsic properties of the ambient space.
mathematically as a sphere instead of ellipsoid for maps at smaller scales. In practice, maps at scale 1:5 000 000 or smaller can use the mathematically simpler sphere without the risk of large distortions. At larger scales, the more complicated mathematics of ellipsoids are needed to prevent these distortions in the map. A sphere can be derived from the certain ellipsoid corresponding either to the semi-major or semi-minor axis, or average of both axes or can have equal volume or equal surface than the ellipsoid [Knippers, 2009].
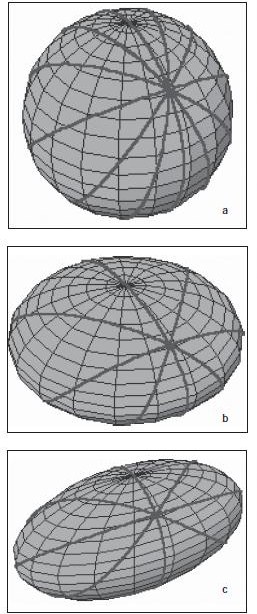
We recall the great circle is the equivalent of the Euclidean straight line, it has the finite distance and it is closed. The geodesics starting from a given position on three main modelling surfaces (2-dimensional modelling manifolds of positive curvature), i.e. sphere, spheroid and triaxial ellipsoid are presented in Fig. 5. The general question we ask affects the range and point of usage of the rhumb line in case the ECDIS systems equipped with the great circle or great ellipse approximation algorithms of given accuracy replaces the traditional paper charts based on Mercator projection.
Figure 5. Geodesics coming from an initial position P on 2-dimensional modelling manifolds of positive curvature a)sphere, b) spheroid (ellipsoid of revolution), c) triaxial ellipsoid.
Moreover, the navigation based on geodesic lines and connected software of the ship’s device (electronic chart, positioning and steering systems) gives a strong argument to use this method for calculations instead of the loxodromic one in general. Although the basic solutions for navigational purposes have already been known and widely used there are still the new approaches and efforts made to the subject. The main efforts affect the optimization and approximation methods which potentially may give the practical benefits for the navigators. As we mentioned above the shortest path between two points on a smooth surface is called a geodesic curve on the surface. Remarkably the path taken by a particle sliding without friction on a surface will always be a geodesic. This is because a defining characteristic of a geodesic is that at each point on its path, the local centre of curvature always lies in the direction of the surface normal, i.e. in the direction of any constrained force required to keep the particle on the surface. There are thus no forces in the local tangent plane of the surface to deflect the particle from its geodesic path. There is a general procedure, using the calculus of variations, to find the equation for geodesics given the metric of the surface [Williams, 1996]. Obviously the Earth is not an exact ellipsoid and deviations from this shape are continually evaluated. The geoid is the name given to the shape that the Earth would assume if it were all measured at mean sea level. This is an undulating surface that varies not more than about a hundred meters above or below a well-fitting ellipsoid, a variation far less than the ellipsoid varies from the sphere. The choice of the reference ellipsoid used for various regions of the Earth has been influenced by the local geoid, but large-scale map projections are designed to fit the reference ellipsoid, not the geoid.
To be concluded in June 2011.
My Coordinates |
EDITORIAL |
|
Mark your calendar |
MAY 2011 TO AUGUST 2011 |
|
News |
INDUSTRY | LBS | GPS | GIS | REMOTE SENSING | GALILEO UPDATE |

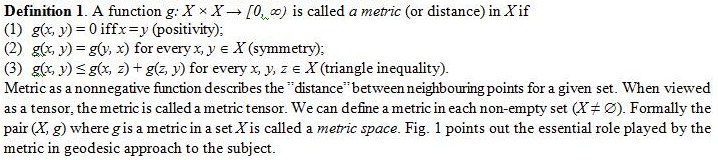













 (5 votes, average: 4.20 out of 5)
(5 votes, average: 4.20 out of 5)





Leave your response!