| Perspective | |
Humorous science: Vampires and zombies
As the world continues to struggle with the COVID-19 pandemic, this paper highlights humorous research showcasing the considerable contribution of vampires and zombies to science |
 |
|
This is the third in a series of papers celebrating some of the weird and wonderful research findings hidden amongst the scientific literature. It aims to ensure that we remember the funnier side of science and provides answers to questions we may have been too afraid to ask. This study was conducted entirely in the author’s spare time and is in no way related to his employer. Here, we explore the fascinating world of vampires and zombies, and their contribution to solving scientific problems.
Vampires
Humans have been interested in vampirology for a long time, presumably caused in part by the fear of potentially not being on top of the food chain. Representing the use of serious analysis of an imaginary topic, several papers studied the coexistence of humans and vampires based on common predatorprey interactions but as a special case because the prey is turned into predator. Hartl and Mehlmann (1982) investigated a typical problem of renewable resources, using mathematical optimisation and control theory to model a dynamic confrontation between humans and vampires. Most interestingly, this was done from the vampires’ point of view.
It was assumed that every living person who had their blood sucked by a vampire would (after their immediate death) turn into a vampire and deal with other persons in the same manner. Considering vampire attrition due to contact with sunlight, crucifixes, garlic and vampire hunters, bloodsucking strategies were mathematically derived for the asymptotically satisfied vampire, the blood maximising vampire and the unsatiable vampire. This represented a typical consumption-resource trade-off: The vampire population derives utility from consumption of human blood, and by turning each victim into a vampire the human resource is reduced while the vampire population increases. The authors basically provided operationsresearch advice to vampires, indicating how vampires could manage their human resources to keep the human race (and thus their own) in existence. The results made it obvious that humans required a defensive strategy against optimally behaving vampires.
Snower (1982) was rather shocked by these efforts and developed a macroeconomic optimal strategy for the destruction of vampires. Intuitively, vampires are like an infectious disease and should be eliminated swiftly and without mercy to avoid a world pandemic. He provided humans with a decision rule of optimally splitting their economy’s output between consumption and production of defensive weapons against vampires. However, by standard application of the maximum principle, he surprisingly concluded that it is socially undesirable to drive the vampire population to extinction.
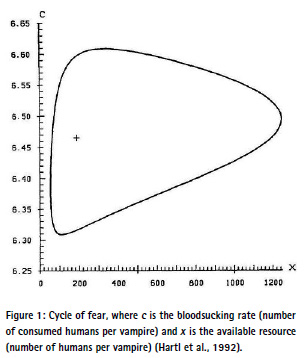
Revisiting the problem, Hartl et al. (1992) improved their model by assuming that changing bloodsucking behaviour induces costs and vampires also derive benefit from possessing humans, not only from consuming them. They mathematically showed that optimal bloodsucking rates change periodically, being modulated over time to achieve a stable tradeoff and net utility according to the so- called cycles of fear, which is more concurrent with empirical evidence in popular literature where the appearance of vampires typically follows a cyclical behaviour. Moving around the cycle of fear (Figure 1) in anti-clockwise direction, the bloodsucking rate increases with the availability of humans per vampire until the resource becomes scarce due to the increasing vampire population, causing a sudden fall in the bloodsucking rate (and the number of vampires) until the human population has recovered sufficiently to sustain an increasing vampire population again.
Using a different approach, Strielkowski et al. (2012, 2013) modelled the humanvampire problem based on popular fiction literature, comic books, movies and TV series in order to determine whether peaceful coexistence of humans and vampires would be scientifically possible.
They identified and investigated four types of scenarios:
• Stoker-King model (based on Bram Stoker’s Dracula and Stephen King’s Salem’s Lot): The vampire requires to be invited by the victim to enter the premises, unless it attacks a sleeping victim. The vampire bites the victim and drinks its blood, then returns to feed for 4-5 consecutive days, at which point the victim dies, is buried and rises to become another vampire (unless a wooden stake is put through its heart). Vampires generally need to feed every day, and there are no organised groups of vampire slayers. This model is very similar to an epidemic outbreak caused by a deadly virus.
• Rice model (based on Anne Rice’s Vampire Chronicles): Vampires act more discreetly, being able to feed on a victim but leaving it to live. Turning a human into a vampire takes time and effort (the victim needs to give permission, drink some of the vampire’s blood, and the process is painful for both). Vampires do not need to feed every day, only requiring some blood once a week or so to survive. There are no organised groups of vampire slayers.
• Harris-Meyer-Kostova model (based on Stephenie Meyer’s Twilight saga, Charlaine Harris’ Sookie Stockhouse (Southern Vampire) book series that inspired the True Blood TV series, and Elizabeth Kostova’s The Historian): Both species coexist and may be aware of each other. Vampires can tolerate the sunlight, drink animal blood to survive or buy bottled synthetic blood. Turning a human into a vampire takes time and effort. Some humans capture and kill vampires to use their blood as a hallucinogenic drug.
• Whedon model (based on the TV series Buffy the Vampire Slayer): Vampires bite the victim, quickly turning it into another vampire. Luckily for humans, there are organised groups of vampire slayers with higher effectiveness than in the Harris-Meyer- Kostova model.
Mathematical modelling showed the Stoker-King model to be highly unrealistic as vampires would need only 6 months to deplete all human resources, thereby causing their own demise. The Rice model merely delayed human extinction to almost 50 years, allowing coexistence only while the vampire population is small. Under certain conditions, the Harris-Meyer- Kostova model appeared to be plausible but very fragile, breaking down when the human population growth slows, the blood thirst of vampires accelerates or the small group of vampire slayers becomes too greedy. The Whedon model was deemed too unstable to be realistic, allowing coexistence only for a short time before vampire slayers exterminate all vampires.
Rather than basing his analysis on the attributes and decisions of representative agents to capture the important characteristics of the economy from the top down as applied in the previously mentioned studies, Farhat (2013) analysed human-vampire interaction from the bottom up. He constructed a computational model in which diverse, artificially intelligent human and vampire individuals (agents) engage in one-on-one interaction according to pre-determined behavioural rules within a virtual landscape.
This revealed that in virtual societies where vampires are highly visible, the human population suffers terribly for a short time (building up defences, which results in starvation) until the vampire population is driven to extinction. In virtual societies where vampires are observable but somewhat hidden, they may flourish provided they are easily destroyed in a confrontation. Cycles of fear then emerge. Otherwise, they increase in numbers, over-exploit the human herd and then starve. In virtual societies where vampires are unobservable, their existence persists. Whether they flourish or stagnate depends on their hunger for blood and the speed of human reproduction. If vampires live on the brink of starvation, both populations continually grow despite mild cycles of fear. If humans reproduce easily, both communities languish with extreme cycles of fear to keep both populations in check. Given our persistent population growth and vampires being rarely encountered today, the former appeared more likely.
Menuet and Villieu (2015) applied the human-vampire problem to the world of finance via a macroeconomic system based on the evolution of public debt and private capital. The debt burden acts as a vampire bite, which reduces available resources for productive public spending in the government budget constraint and lowers both the output and rate of capital accumulation. Simultaneously, the collection of income tax vanishes, generating further increases in public debt. Therefore, the public-debt vampire transforms privatecapital humans into its own kind, sucking the productive flow of public expenditure and regenerating by weakening the government’s fiscal stance. The optimal rate of depletion of non-infected capital (the consumption of goods or harvesting of humans) was then obtained from a standard optimal control problem. In agreement with Snower (1982), it was shown that the extinction of the public-debt vampire is suboptimal because this would involve fixing the tax rate at such a level that economic growth would deteriorate too much.
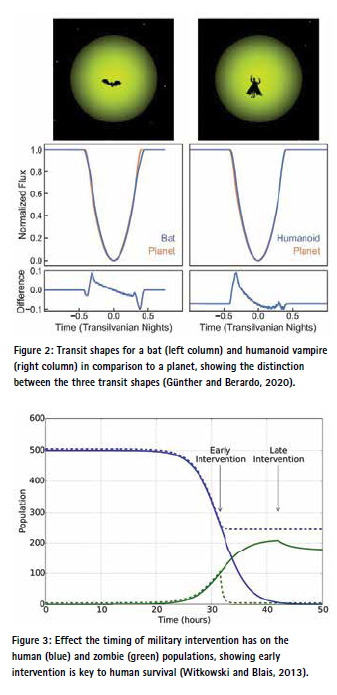
Looking further afield and moving on to astronomy, Günther and Berardo (2020) reported on the search for transit signatures of space vampires trapped in the gravitational pull of cool dwarf stars. This research supports the theory that vampires may have originated in outer space, settled down and domesticated asteroids, and then fell onto Earth through meteor crashes. The authors generated models representing two potential space vampire populations (i.e. bat shape and humanoid shape) and searched light curves from the Transiting Exo- Vampire Survey Satellite (TEVSS) using a template matching algorithm. This clearly showed the distinction between the transit shapes of bats and humanoid space vampires compared to planets void of these creatures (Figure 2).
Analysis of the TEVSS data provided a short list of between 0 and 394,400,933 potential space vampire transits. Using Bayesian evidence, they determined that two of these most likely originated from bats (or noise) and one from a humanoid shape (or noise), while the remainder could be due to either shape (or noise). Adding the information gained from TEVSS data constrained the space vampire occurrence rate to between 0% and 100%. It was noted that such precise analyses will be crucial in optimising future observing schedules for space-vampire characterisation with the James Webb Space-Vampire Telescope (JWSVT) and the Extremely-Large-Vampire Telescopes (ELVTs).
Zombies
Zombies move in small, irregular steps and show signs of physical decomposition such as rotting flesh, discoloured eyes and open wounds. Due to their inferior intelligence and sophistication, zombies may not be as attractive to the science community as vampires. However, their insatiable hunger for living human flesh and ability to turn humans into zombies by inflicting a bite is very similar to the Stoker-King vampire model and an ideal setting to investigate scenarios of an infectious disease outbreak.
Munz et al. (2009) were the first to apply mathematical modelling to the analysis of a zombie outbreak by using an epidemiological model to investigate the dynamics of a zombie apocalypse. In this case, zombies are created either by infection of a living human or resurrection of recently deceased humans. The latter was acknowledged to be an unlikely scenario if taken literally, but possible reallife applications may include allegiance to political parties or diseases with a dormant infection. Zombification can be avoided by defeating the zombie during a confrontation, e.g. by destroying its brain, decapitation or cremation.
The analysis included a latent period of zombification, whereby humans are infected but not infectious before becoming undead. It was shown that quarantine of infected and zombified individuals would only delay the inevitable doomsday scenario, i.e. the collapse of society as zombies take over the planet. A cure, allowing zombies to return to their human form but not providing immunity to repeated infection, would result in a small human population surviving the outbreak while still coexisting with zombies. Only sufficiently frequent attacks, with increasing force, would result in the eradication of zombies, assuming the available resources can be mustered in time.
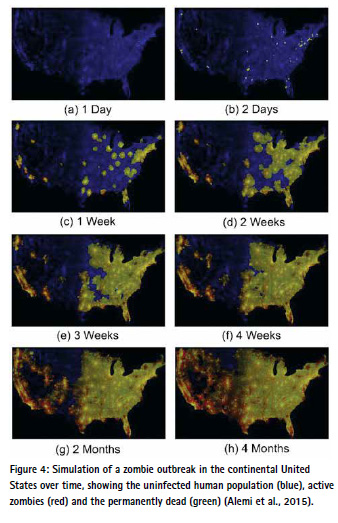
Several others extended this work. For example, Witkowski and Blais (2013) introduced tools of Bayesian statistics, removed zombification via resurrection and used quantitative data (zombie population estimates taken from depictions of zombies in popular movies) to estimate the dynamic model parameters. The same model was then applied to actual data on influenza to establish infection and recovery rates, thus making the methods more applicable to real-world disease dynamics. The popular movies Night of the Living Dead and Shaun of the Dead were analysed in detail, both including a military intervention that saves human civilisation. It was shown that the strength and timing of the attack are crucial for its success. If the intervention happens quickly, the zombie population is effectively eliminated. However, if it happens later, intervention of any magnitude may be in vain (Figure 3).
Considering several model variants and employing spatial parameters, Alemi et al. (2015) provided a full-scale stochastic dynamic simulation of a zombie outbreak in the continental United States (Figure 4). The simulation started with one in every million individuals being infected at random. By the first week, most of the population had been turned into zombies, although the map does not appear that compelling. In the early stages, the outbreak spread in roughly uniform circles, with the speed of infection tied to the local population density. Infections on the coasts (higher population density) reached further than those near the centre of the country. After several weeks, the map shows stronger diversity in the directional spread, now over larger geographical areas and influenced by large changes in population density. After 4 weeks, much of the country had been overrun, but remote areas remained zombie-free even after 4 months.
Zombie danger maps were also produced, showing the probability of being infected at a certain location and point in time during an epidemic originating from a single zombie. As expected, after 7 days, high-population metropolitan areas are most at risk because many individuals could potentially serve as patient zero and zombies rapidly spread in these areas. After 28 days, it is not the largest metropolitan areas that suffer the greatest risk of being overrun but the regions located between them.
Using a far more general approach based on elementary physics and mathematics, Efthimiou and Gandhi (2007) attempted to prove that these creatures do not exist, promptly attracting criticism regarding the simplicity of the argumentation used (Sejdinovic, 2008). However, their intent was to provoke critical thinking and encourage probability-based assessments of various claims using reason, reminding readers that pseudoscientific and paranormal ideas generally make no sense when elementary logic and science is applied and that any element of truth is usually distorted and hidden behind elaborate myths.
To this end, sudden drops in temperature when sensing a ghostly presence in an old building were explained by the draught of air through concealed doors, causing columns of cold air to emerge. Newton’s laws of motion were then used to highlight the paradox that ghosts can apparently walk around (and therefore must be material) but pass through walls and are unable to pick up objects (and therefore must be immaterial). The existence of vampires was disproved by basic calculations showing that humanity would become extinct about 2.5 years after the first vampire appears. The same argument was applied to zombies in popular literature and movies. A documented case of voodoo zombification (where zombies are created by a sorcerer’s spell) was explained by the use of a puffer fish toxin, which suspends the victim’s bodily functions and causes them to appear dead. After being buried alive, oxygen deprivation damages the brain. If the person is unburied (or manages to escape the grave) before really dying from suffocation, they appear as a soulless creature (zombie) because they have lost the thinking process of their brain.
Conclusion
These selected studies have demonstrated the flexibility of mathematical modelling and how it can respond to a wide range of challenges for different areas of science, tongue in cheek or not. They have also highlighted that modelling output is heavily reliant on the assumptions made and the input parameters chosen. Amusing examples can improve student learning of a topic and make it more accessible to an outside audience, thereby contributing to a better understanding of science in the general public.
Entertaining outreach programs can help attract potential students into Science, Technology, Engineering and Maths (STEM) and related disciplines. For example, Curtin University’s Team Zombie is a multi-disciplinary response team that investigates a zombie outbreak, models the spread and potential interventions, works towards cures or vaccines, and provides options for detection and monitoring. Engaging students from primary school through to university level, it is raising awareness of the many approaches to problem solving through models and simulations (Maxville and Sandford, 2020).
References
Alemi A.A., Bierbaum M., Myers C.R. and Sethna J.P. (2015) You can run, you can hide: The epidemiology and statistical mechanics of zombies, Physical Review E, 92(5), 052801.
Efthimiou C.J. and Gandhi S. (2007) Cinema fiction vs. physics reality: Ghosts, vampires and zombies, Skeptical Inquirer, 31(4), 27-34.
Farhat D. (2013) The economics of vampires: An agent-based perspective, Economics Discussion Papers No. 1301, University of Otago, New Zealand, 23pp.
Günther M.N. and Berardo D.A. (2020) Searching for space vampires with TEVSS, https://arxiv.org/ abs/2003.14345 (accessed Oct 2021).
Hartl R. and Mehlmann A. (1982) The Transylvanian problem of renewable resources, Operations Research, 16(4), 379-390.
Hartl R.F., Mehlmann A. and Novak A. (1992) Cycles of fear: Periodic bloodsucking rates for vampires, Journal of Optimization Theory and Applications, 75(3), 559-568.
Maxville V. and Sandford B. (2020) Computational science vs. zombies, in Krzhizhanovskaya V.V. et al. (eds.) Computational science – ICCS 2020, Lecture Notes in Computer Science, vol. 12143, Springer, Cham, 622-633.
Menuet M. and Villieu P. (2015) Is government debt a vamp? Public finance in a Transylvanian growth model, https://hal.inria.fr/ halshs-01199770/ (accessed Oct 2021).
Munz P., Hudea I., Imad J. and Smith? R.J. (2009) When zombies attack!: Mathematical modelling of an outbreak of zombie infection, in Tchuenche J.M. and Chiyaka C. (eds.) Infectious disease modelling research progress, Nova Science Publishers, Hauppauge, 133-150.
Sejdinovic D. (2008) Mathematics of the human-vampire conflict, Math Horizons, 16(2), 14-15.
Snower D.J. (1982) Macroeconomic policy and the optimal destruction of vampires, Journal of Political Economy, 90(3), 647-655.
Strielkowski W., Lisin E. and Welkins E. (2012) Intertemporal model of coexistence of two rival species: A case of vampires and humans co-habitation, Modern Economy, 3(7), 826-831.
Strielkowski W., Lisin E. and Welkins E. (2013) Mathematical models of interactions between species: Peaceful co-existence of vampires and humans based on the models derived from fiction literature and films, Applied Mathematical Sciences, 7(10), 453-470.
Witkowski C. and Blais B. (2013) Bayesian analysis of epidemics – Zombies, influenza, and other diseases, http://arxiv.org/abs/1311.6376 (accessed Oct 2021).











 (No Ratings Yet)
(No Ratings Yet)






Leave your response!