Contact | Previous Issues | Articles-by-Author

GPS based control points for mapping

Oct 2006 | Comments Off

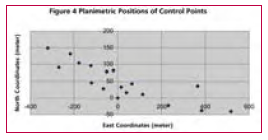
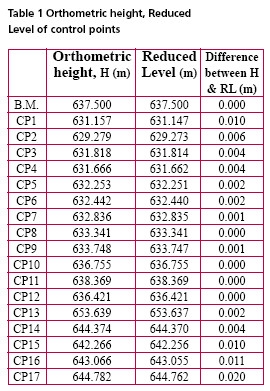
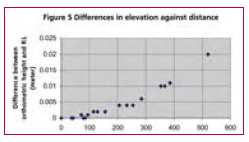
Observation and Result

The observation was taken on December 29, 2002 starting from 09hr 31min 55sec to 16hr 46min 55sec i.e., a duration of 7 hr 15 min starting from morning to evening. On next day i.e, on December 30, 2002 the observation session started at morning (08 hr 31 min 30 sec) and continued till evening (14 hr 32min 25 sec) for a duration of 6 hr 12 min 55 sec. The observed data was processed in SKI 2.3 in relative positioning mode. Dual frequency data were used in processing. Broadcast ephemerides were used to compute the position of satellite. Hopfield model was used to take into consideration the delay caused by troposphere but no model was used for ionospheric interference. After processing the data, positions of the B.M. and other control points have been found in WGS 84 coordinate system.

The global coordinates thus found are then converted to local Cartesian Coordinates (Topocentric System) with origin at B.M. using the Equation (10). The local Cartesian Coordinates of the control points are obtained considering B.M. as origin. A plot of the planimetric position of the control points is as shown in Figure 4.

To find the vertical position of the control points two types of heights i.e., orthometric height and reduced level have been found. The concept of datum transformation (Hofmann- Wellenhoff, 2001) has been used to find orthometric height. In this, first the amount of geodetic undulation at the B.M. is calculated from geodetic height (606.794 meter, found from GPS obsevation) and the orthometric height (637.5000 meter) as established field data. This has been found to be 30.706 meter (637.500- 606.794). The reduced level (R.L.) of the control points are calculated using the R.L. of the B.M (637.5000 meter) and the difference in vertical elevation (z) between the B.M. and that of considered control point [as found by the transformation equation (10) given in Table 1, the z component]. The orthometric height and the R.L. of all the control points thus obtained are as shown in Table 1.

Discussion

To minimize the inherent errors associated with in GPS observations (Leick, 1995) due precausion had been taken all throughout the campaign. Moreover, observations were taken in relative positioning mode and the area surveyed is small thus it has been assumed that the residual error, if any, is the same for all points.

The topo-centric local grid coordinates of control points are calculated from GPS observation. A transformation matrix based on geodetic coordinates of the origin (based on GPS observation in the global geodetic system) has been used and no other data is required for finding out the planimetric positions. The vertical height of points are also found from the same GPS observation. Thus, all the three components of the position of any control point are based on same set of GPS observation. This helps in minimizing the field work drastically over the traditional methods.

The elevation of points has been found by adopting two independent methods using the same set of GPS observation. First one is the method of datum transformation. In this method, the orthometric heights of points have been found. Since, the distance between origin and other points are small with respect to geodetic consideration, it has been assumed that the difference in the angle of deflection to vertical (e) between the origin and other points is negligibly small. Next, the reduced level (vertical elevation) of control points are calculated using the vertical height (found by transformation matrix) and R.L. of B.M. These heights are found to be mostly equal to that of orthometric heights. The deviations of R.L. from orthometric heights within the study area noted to be increasing with the distance from origin (Figure 5) but do not depend on the height of points above origin (figure 6). Thus, the variation in heights may be attributed to the variation in geodetic undulation with distance, as expected since the terrain is hilly.

Further, the grid coordinates thus calculated can easily be related to other local or global network as the considered directions (north, East and vertical) of axes are universal and origin (B.M.) is well established.

Conclusion

Transformation of GPS observation will help cartographers by providing a topo-centric coordinate system with B.M. as origin. This method results in very accurate positioning of control points for a small area. This method is quite simple and easier than conventional transformation methods. Moreover, this will lead to overcome the problem of non-availability of precise geodetic coordinates of control points. Determination of vertical height of points is quite simple. However, to restrict the amount of accuracy within desired limit, the variation of geodetic undulation at the site is to found before further surveying operation. The areal extent to which the undulation deviates from that of the origin within the permissible limit (depending on the desire accuracy of the campaign) first better be determined. Thus, if area to be surveyed is large and the desired accuracy is high, a number of bench marks are required to be available in the site or to be established first and subsequently, the command area for mapping using GPS observation around the bench marks are to be found.

Acknowledgement

Students of B.Tech (2002-2003) Final year (Civil) of IIT Roorkee for collecting the data. Authors also acknowledge the help rendered by Prof A.K.Mathur and Dr. M.Singh in organizing the survey campaign successfully.