| Geodesy | |
Geopotential models and their application in local geoid modelling
The objective of this article is to share the knowledge of alternative way of geoid determination with incorporating a high resolution GGM, terrain and GPS/levelling data |
 |
|
Development of GGMs
With the advent of new gravity dedicated satellite missions (CHAMP, GRACE and GOCE), the long wavelength gravity field modeling of the Earth is possible with remarkable accuracy. Numerous global geopotential models (GGMs) have been developed to date with these improved satellite gravity information, enhanced land gravity and satellite altimeter data. These GGMs can be categorized into: CHAMP-only (TEG4 (Tapley et al., 2001), , EIGEN-2 (Reigber et al., 2003)), GRACE-only (ITG-Grace03 (Mayer-Gürr etal., 2007), EGM2008 (Pavlis et al., 2012)), GOCE-only (GO_CONS_GCF_2_SPW_R2 (Migliaccio et al., 2010)), and their combinations with terrestrial gravity and altimeter data (EIGEN-6C (EIGEN-6C4 (Foerste et al. 2014), GECO (Gilardoni et al. 2016); SGG-UGM-1(Weiet al. 2018), SGG-UGM-2 (Weiet al. 2020)). All developed GGMs to date are available at http://icgem.gfz-potsdam.de/ICGEM/ICGEM.html.
High resolution GGMs and EGM2008
The EGM2008 represents the first state-of-the-art global high resolution model publicly released by the U.S. National Geospatial-Intelligence Agency (NGA) EGM Development Team in April 2008 (Pavlis et al., 2012: http://earth-info.nga.mil/GandG/wgs84/ gravitymod/egm2008/index.html).The development of this model is a major achievement in global gravity field modeling. It completes spherical harmonic degree and order 2160, and provides some additional coefficients up to degree 2190. These represent

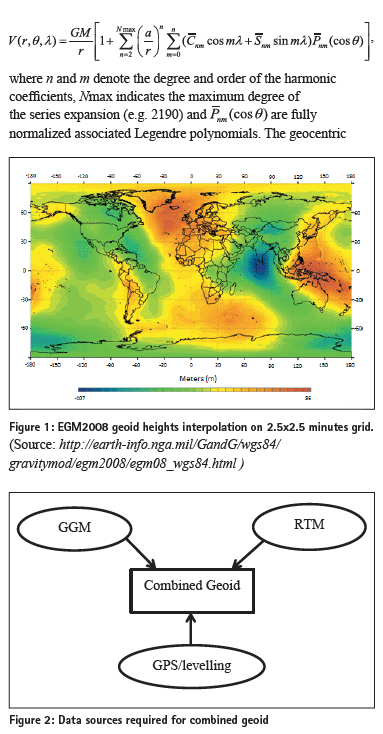
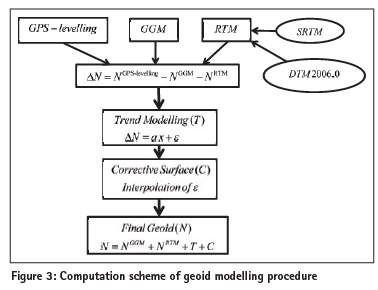

Geoid modelling using high resolution GGM and terrain data
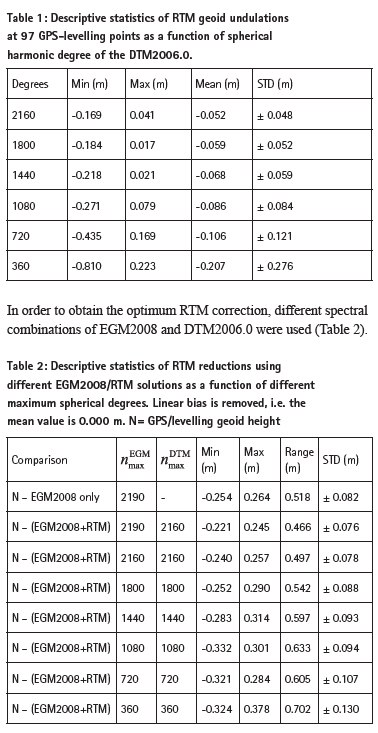
In remove-restore approach of gravimetric geoid determination, the geoid undulations due to long wavelength gravity fi eld variations are estimated by a GGM and the high frequency components are obtained through a regional topographic model. The remaining medium to short wavelength features of geoid undulations are estimated by Stokes or Molodenskybased approaches using gravity measurements. With the availability of high resolution GGM, separate estimation of medium level components became unnecessary since medium and even part of the short wavelength components are already embedded in high resolution GGM. Therefore, as an alternative methodology, combined geoid determination using heterogeneous data can be used for local geoid modelling.
The truncation of GGM model at its maximum degree and order leads to omission (truncation) errors, and can contribute to the fact that the model is unable to resolve all gravity fi eld features, from the long to the short wavelength. This error is more evident in mountainous regions where the topography is the dominant source of the short wavelength features of the gravitational field. If it is possible to estimate the effect of the omission errors on geoid heights, then the effect can be added to GGM derived geoid heights to obtain improved geoid heights, especially in mountainous areas (Hirt et al. 2010, Prasanna et al. 2021). The available GPS-levelling data can then be used to constrain long wavelength geoid errors. In practical geoid determination schemes, a GGM is used as a reference field, which includes the effect of global topography. The RTM reduction method (Forsberg 1984) accounts for the topographic irregularities relative to smooth reference surface. The advantage of RTM method is that it only accounts for the topographic effect that has not been included in the spherical harmonic model of the gravity fi eld of the Earth.
RTM geoid heights


RTM elevations can be converted to the corresponding geoid heights NRTM using the rectangular prism forward modelling method (Nagy et al. 2000).
The available GPS-levelling data can then be used to constrain long wavelength geoid errors (ΔN) that can be estimated through a low order trend function.

Numerical results
Geoid modelling in Canadian Rockies (Prasanna & Chen, 2012):

A part of the Canadian Rockies (latitude 49o-53o -N and longitude 118o-114o W, 300x450km2) was selected as the test area. It comprises rough mountains with elevation variation from 400m to 3500m and reasonable numbers of GPS-levelling points are available for computation (Figure 4).
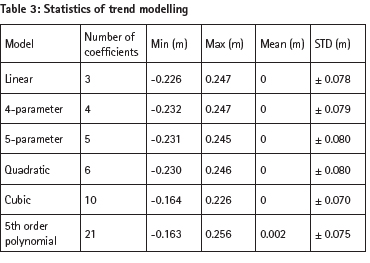
EGM2008 geoid model was used as the high resolution GGM. There are significant omission errors in EGM2008 in this mountainous area. The RTM corrections were estimated as the difference between high resolution SRTM3 and the low resolution DTM2006.0 models. As DTM2006.0 is the topography model incorporated in EGM2008, the RTM corrections represent the fine geoid features which are not included in the EGM2008 model. Table 1 shows the RTM corrections as the as a function of spherical harmonic degree of the DTM2006.0.
In order to obtain the optimum RTM correction, different spectral combinations of EGM2008 and DTM2006.0 were used (Table 2).
According to the Table 2, RTM correction with respect to the maximum spherical harmonic degree 2190 of EGM2008 and 2160 of DTM2006.0 reference surfaces seems optimum in terms of the residual range and the standard deviation.
A parametric model was used to compute the trend which comprises systematic part of ΔΝ. Table 3 shows the results after the trend modeling and the cubic function gives slightly better results.
The detrended residuals obtained from the cubic model are interpolated using various interpolation techniques. Among those techniques, the kriging and minimum curvature interpolation methods shows good results.
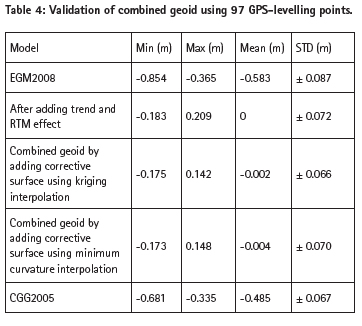
The final combined geoid is obtained by adding corrective surface, cubic trend and RTM effect to the EGM2008 geoid heights. Figure 5 shows the combined EGM2008 geoid over the test area. Table 4 shows the validation of the combined geoid and comparison with the Canadian CGG2005 geoid.
Conclusions
The objective of this article is to share the knowledge of alternative way of geoid determination with incorporating a high resolution GGM, terrain and GPS/levelling data. This method would be useful for regions with sparse GPS-levelling and gravity data networks.
The test area selected was a well surveyed area with very large elevation variations (400 to 3500 m). The omission error of EGM2008 in the region was quite large and thus suitable for testing the proposed alternative method.
References
Farr, T. G., Rosen, P. A., Caro, E., Crippen, R., Duren, R., Hensley, S., et al. (2007). The ShuttleRadarTopography mission. Revgeophys, 4, RG2004.
Foerste, C., S. L. Bruinsma, O. Abrikosov, J. Lemoine, J. Marty, F. Flechtner, G. Balmino,
F. Barthelmes, and R. Biancale. 2014. EIGEN-6C4: The latest combined global gravity
MARINE GEODESY 17 field model including GOCE data up to degree and order 2190 of GFZ Potsdam and GRGS Toulouse. GFZ Data Services.
Gilardoni, M., M. Reguzzoni, and D. Sampietro. 2016. GECO: A global gravity model by locally combining GOCE data and EGM2008. Studia Geophysica et Geodaetica 60 (2):228–47. 2016.
Hirt, C., Featherstone, W. E. and Marti, U. (2010). Combining EGM2008 and SRTM/DTM2006.0 residual terrain model data to improve quasigeoid computations in mountainous areas devoid of gravity data. Journal of Geodesy, 84(9), 557-567.
Mayer-Gürr, T. (2007). ITG-Grace03s: The latest GRACE gravity field solution computed in Bonn. Joint International GSTM and DFG SPP Symposium, 15.
Migliaccio, F., Reguzzoni, M., Sansò, F., Tscherning, C. C. and Veicherts, M. (2010). GOCE data analysis: The space-wise approach and the first space-wise gravity field model. Proceedings of the ESA Living Planet Symposium, 28.
Nagy, D., Papp, G. and Benedek, J. (2000). The gravitational potential and its derivatives for the prism. Journal of Geodesy, 74(7-8), 552–560.
Pavlis, N. K., Factor, J. K. and Holmes, S. A. (2007). Terrain-related gravimetric quantities computed for the next EGM.in: Forsberg R, kiliçoğlu A (eds). 1st International Symposium of the International Gravity Field Service, Gravity Field of the Earth, General Command of Mapping, (Special issue18), 318-323.
Pavlis, N. K., Holmes, S. A., Kenyon, S. C. and Factor, J. K. (2012). The development and evaluation of the Earth Gravitational Model 2008 (EGM2008). Journal of Geophysical Research: Solid Earth (1978–2012), 117(B4).
Prasanna, H. M. I. and Chen, W. (2012). Geoid modeling using a high resolution geopotential model and terrain data: A case study in Canadian Rockies. Journal of Applied Geodesy, 6 (2), 89-101.
Prasanna, H. M. I., Gunathilaka, M. D. E. K, & Welikanna, D. R. (2021). Development of a unified vertical reference framework for Land and Hydrographic surveying in Sri Lanka. Marine Geodesy, 1-13. DOI:10.1080/01490419.2021.1902889
Reigber, C., Schwintzer, P., Neumayer, K., Barthelmes, F., König, R., Förste, C., et al. (2003). The CHAMP-only earth gravity field model EIGEN-2. Advances in Space Research, 31(8), 1883-1888.
Tapley, B., Bettadpur, S., Chambers, D., Cheng, M., Gunter, B., Kang, Z., et al. (2001). Gravity field determination from CHAMP using GPS tracking and accelerometer data: Initial results. AGU Fall Meeting Abstracts, 1. pp. 02-36.
Wei, L. X. U., Xinyu, L. I., and Jiancheng Z. H. U. Guangbin. 2018. The determination of
an ultra-high gravity field model SGG-UGM-1 by combining EGM2008 gravity anomaly
and GOCE observation data. Acta Geodaetica et Cartographica Sinica 47 (4):425–34.











 (No Ratings Yet)
(No Ratings Yet)






Leave your response!