| Geodesy | |
Geoid modelling
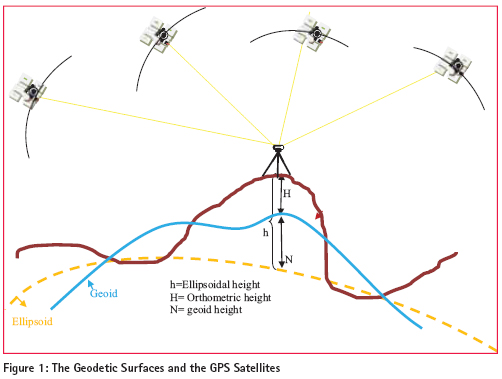
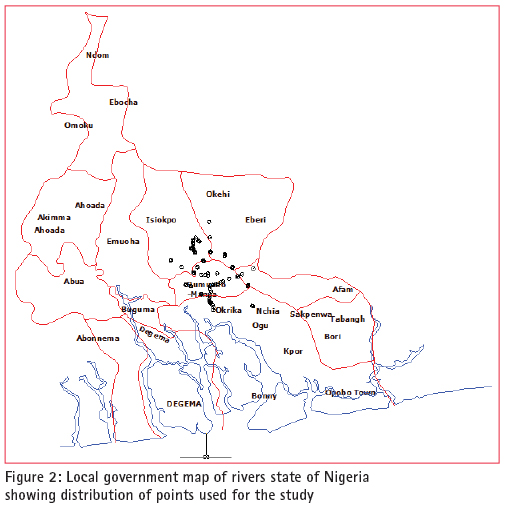
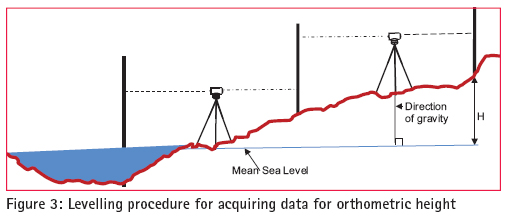
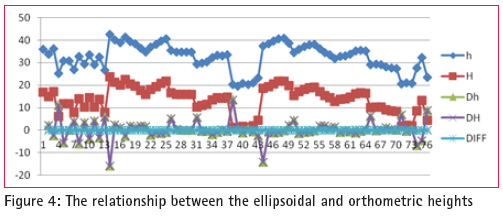
The geoid can be determined using different method such as gravimetric, astro-geodetic, GPS/ Levelling and “satlevel”. ‘Satlevel’ is a new method of geoid determination, in which the ellipsoidal height is used with orthometric height to model the geoid. Geoid modelling is a process of developing mathematical algorithms to represent the geoid. This is the reference surface for orthometric height. Geoid is one of the geodetic surfaces. Geodetic surfaces All activities in surveying are carried on three basic surfaces referred to as geodetic surfaces. These surfaces are: the topographic surface, the geoid and the ellipsoid The topographical surfaceThe Topographical Surface generally called the earth’s surface is the actual surface of the land and sea. This is where all measurements and observations are being carried out. It is an irregular surface and therefore geodetic computation cannot be carried out on this surface. The surface that is closely related to the topographical surface is the geoid. GeoidGeoid comes from the word “geo” literarily means earth-shaped. The geoid is an empirical approximation of the figure of the earth (minus topographic relief). It is corresponding to the Mean Sea Level (MSL) over the oceans. It has a defi nite physical interpretation, in the sense that it can be fi xed by measurements over the ocean with the use of Mean Sea Level. Mean Sea Level (MSL)The surface to which heights of points are referred is called a vertical datum. Traditionally, surveyors and mapmakers have tried to simplify the task by using the average (or mean) of sea level as the defi nition of zero elevation, because the sea surface is available worldwide. The surveyor in the fi eld, levels the instrument with the aid of spirit level, which aligns the plumbline perpendicular to the geoid. Therefore, it is a very good approximation to say that the spirit level is always parallel to the geoid, even if a little way above or below it. MSL can be used to approximate the geoid which can be fi tted to a more regular surface called the ellipsoid. The ellipsoidThe ellipsoid may be defi ned as a surface whose plane sections are all ellipses. One particular ellipsoid of revolution, also called the “normal earth”, is the one having the same angular velocity and the same mass as the actual earth, the potential U0 on the ellipsoid surface equal to the potential (W0) on the geoid, and the centre coincident with the centre of mass of the earth (Xiong et al, 2001. The ellipsoid serves as reference to which the coordinates of satellite systems such as the Global Navigation Satellite System are referred. One of the components of geodetic coordinates is the ellipsoidal height, i.e. the height measured with reference to the ellipsoid; while orthometric height is measured with reference to the geoid. The fastest method of obtaining ellipsoidal height is from satellite methods using Global Navigation Satellite Systems. Global Navigation Satellite System Is the general term referred to the families of satellite based positioning systems like the Global Positioning System (GPS), Glonass, Compass, Indian Regional Navigation Satellites System and Quasi-Zenith Satellite System. Surveys with all these satellites system result in 3D coordinates with reference to a range of reference ellipsoids. GPS provides coordinates using the WGS 84 reference ellipsoid. Ellipsoidal height is not always used because; it does not provide elevation above the MSL which refers to the earth gravity equipotential surface i.e. the geoid, the referenced surface for orthometric heights. There are many reasons which may be accounted for the use of orthometric height. Spirit levelling is the dominant technique for providing elevation above MSL (Orthometric height) (Bomford,1980; Fajemirokun, 1980; Featherstone, 1998; Vanicek, 2001; Fotopoulus, 2003 and Uzodinma, 2005). The equipment is inexpensive and the method is highly accurate. However, it is labour intensive over long distances and the fi eld procedures are tedious and prone to human and other errors. In some areas such as Niger Delta region of Nigeria, it is often impossible to perform spirit levelling due to weather, terrain conditions and swamps. Ellipsoidal height is simpler and easier to obtain with GPS than orthometric height. Combined, the two quantities give the geoid-ellipsoid separation as can seen in the basic equation 1.1. N = h – H (1.1) Where: N = geoid-ellipsoid separation (geoid height) h = Ellipsoidal height H = Orthometric height One of the common problems with height systems in Nigeria is the lack of a uniform reference datum. the MSL is often adopted as the basis for reckoning heights. However, defi ning the mean sea level and carrying it to the hinterland have always been problematic resulting in poor or uncoordinated height systems (Olaleye et al, 2010). Another problem is the failure of some of the existing models to accurately model the Nigerian environment because they are developed to suit a particular area or region hence there is need for a model to meet the challenges. The aim of this research is to develop an empirical geoid model for predicting the undulation values for transforming ellipsoidal heights to orthometric heights and vice versa. Using today’s available technology and techniques, ellipsoidal heights can be obtained from different systems, such as: Very Long Baseline Interferometry (VLBI), Satellite Laser Ranging (SLR), and other navigation based systems such as: Doppler Orbitography by Radio-positioning Integrated on Satellite (DORIS), GPS and GLONASS and satellite altimetry. Ellipsoidal height is one of the 3D components of GPS. Apart from ellipsoidal height, the other information required to implement equation 1.1 is the orthometric height, which has relationship with Mean Sea Level as earlier discussed. This can be practically obtained using geodetic levelling for data acquisition. Study areaThe model was tested using the data acquired in Port Harcourt area of Nigeria. The study area, Port Harcourt lies between latitude: 4°45’ and 5°02’N and between longitude: 6°52E and 7°09’E. Since sufficient data were available to implement Equation 1.1, it is possible to derive a mathematical model such that, with GPS observation, we should be able to compute the geoidal undulation using any regression method, provided it satisfi es certain statistical criteria regarding the data and determining the best fi t to the observations (Younger; 1985). In this case, the least squares approach was used to fi nd the best curve, that is, the one which is on average closest to all points, since blunders in the observations were removed. As a way of checking for arithmetic errors or blunders, the values of the coeffi cients were substituted into the original model and both equations must check. Problems were experienced with regard to the number of decimal places carried causing rounding errors. The new models combined the accuracy of orthometric height and ease of ellipsoidal height in geoid determination to develop the ‘Satlevel’ model. ‘Satlevel’ method of geoid determinationSatlevel method of geoid determination involves the use of both ellipsoidal and orthometric heights to develop a mathematical algorithm to determine the geoid. The methodology involves acquisition of data relating to ellipsoidal and orthometric heights, formulating the problems to develop the model and analysis of results. Field Operations The fi eld operations were carried out for the purposes of acquiring the ellipsoidal heights and orthometric heights for a number of well distributed points in the study area. Both spirit levelling and GPS fi eld exercises were carried out. Spirit levellingEvery survey job must be planned to attain certain accuracy. In this research, fi rst order accuracy was planned and achieved in geodetic levelling. (Davis et al, 1981; SURCON, 2003). GPS observationMethodology of Differential Global Positioning System (DGPS) as given by Trimble (2007) was adopted. DGPS observations were made at the most suitable locations along the levelling routes using a dual frequency GPS receiver (Trimble 4700). The results of the fi eld operation were processed and used for the mathematical modelling. Mathematical model Physical evidence of the views of the surface of the earth supports the hypothesis that the totality of geoidal undulation at a geographic location is composed of two parts, namely: 1) the constant part throughout the study area Nm = X0 (independent of position) and 2) the changing part Nc = f(φ, λ) which depends on changes in geographic location within the study area. N = Nm + Nc (2.1) The statistical signifi cance of these relationships is considered in developing the model. The model assumed that the geoidal undulation is a function of geographical location. The model was derived Where: x1, x2, x3 ,x4 and x5 are the unknown parameters. All other terms as earlier defi ned.The set of base functions for Equation 2.2 were determined and the unknown parameters were estimated using least squares adjustment since suffi cient observation point were available. Results and analysisResult The results of data acquisition of orthometric height (H) from geodetic levelling and that of GPS ellipsoidal heights (h) are presented as shown in figure 1. On the Y-axis are the values of undulations while X-axis contained the numbers given to each of the 76 points used for the study. Dh and DH are the ellipsoidal and orthometric heights differences between successive points respectivelly. DIFF is the height differences between Dh and DH Other terms as defi ned previously. Assessing the parametric model performance The following tests were used to assess the performance of parametric Classical empirical approachThe residuals were computed. The mean square error obtained was 0.134mm Model validationData for fi ve points were randomly selected as checks for model validation. The mean square error computed to be 0.159mm Significance test of the model parametersCoefficient of determinationA statistical measure of the goodness of the parametric model fi t for a discrete set of points is denoted by R2. The coeffi cient of determination for the model was computed as 0.982. Therefore, the variation not accounted for by the model is just 2%. ‘Orthometric Height on Fly’ The model was used to develop a computer program to compute orthometric height from GPS coordinates. ConclusionsIn this study, levelled heights were established and the benchmarks were coordinated and collocated with both GPS and geodetic levelling in the Port Harcourt Metropolis. Optimal predictive geoid models ‘Satlevel’ for deriving orthometric height from ellipsoidal heights on the WGS 84 reference ellipsoid were developed. Analyses were carried out which showed that there is no signifi cant differences between the values obtained with the derived modelled and the observed values. ‘Orthometric Height on Fly’ was developed for converting GPS ellipsoidal height to orthometric height. RecommendationsIt is also recommended that the area of the data be extended as funds become available so that improvement can be made on the models. It will be necessary to carry differential levelling to other parts of Rivers state and indeed, other parts of Nigeria to serve the need of Surveyors and Engineers. ReferencesAyeni, O. O. (2001) Statistical adjustment and analysis of data with application in surveying and Photogrammetry. Lagos, Nigeria: University of Lagos. Bomford G (1980) Geodesy (fourth edition), Clarendon press. London Featherstone, W. E. (1996) An analysis of GPS height determination in Western Australia, The Australian Surveyor, pp. 29- 34 www.cage.curtin.edu.au/~will/SSC2007 Deakin R. E. (1996) The Geoid, What’s it got to do with me? The Australian Surveyor, 41(4): 294 – 303 Fajemirokun, F. A.(1980) The Nigerian geodetic control system: An appraisal. Proceedings of the XVth Annual General Meeting of the Nigerian Institution of Surveyors held in Abeokuta. 22nd – 24th April. Moka, E. C. & Agajelu S. I. (2006) On the problems of computing orthometric heights from GPS data. Proceedings of the 1st international workshop on geodesy & geodynamics, Toro, Bauchi State, Nigeria, pp. 85 – 91. Olaleye, J. B., K. F. Aleem, J. O. Olusina and O. E. Abiodun (2010) Establishment of an . empirical geoid model for a small geographic area: A case study of Port, Harcourt, Nigeria. Surveying and Land Information, Science.70(1):39-48(10) http://www. Ingentaconnect .com/content/nsps/ salis/2010/00000070/00000001/art00006 Roberts, C. (2011) How will all the new GNSS signals help RTK surveyors?, Proceedings of the Spatial Sciences & Surveying Biennial Conference, Wellington, New Zealand, 21 – 25 Nov. Rüeger, J.M. (1998) Is levelling out of date?, Proceedings of the ACSM conference, Baltimore, Maryland, USA, Vol 1, pp 216 – 226. Trimble Navigation Ltd.(2007) GPS: The fi rst global navigation satellite system. Sunnyvale, California: Trimble Navigation Ltd. Part number 36238- 00 version 1.0 Uzodinma N. V. (2005) “VLBI, SLR and GPS data in the Nigerian primary triangulation… network – what benefi ts to future research and the national economy?, Proceeding of 1st international workshop on geodesy and geodynamics. Centre for Geodesy and Geodynamics, Toro, Nigeria. Feb 5th to 10th Xiong Li and Hans-Jürgen Götzez (2001) Ellipsoid, geoid, gravity, geodesy, and geophysics. Journal of geophysics. 66 (6): 1660-1668. Younger, M. S. (1989) A fi rst course in linear regression.(second Edition), PWS Publishers, Boston, USA.
|



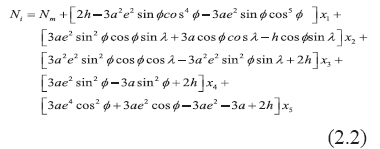












 (2 votes, average: 1.00 out of 5)
(2 votes, average: 1.00 out of 5)



Leave your response!