Choosing the best path: Global to national coordinate transformations

Joel Haasdyk GNSS Surveyor, NSW Land and Property Information, Bathurst, Australia

Dr Volker Janssen GNSS Surveyor, NSW Land and Property Information, Bathurst, Australia

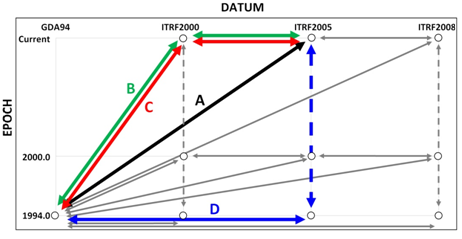
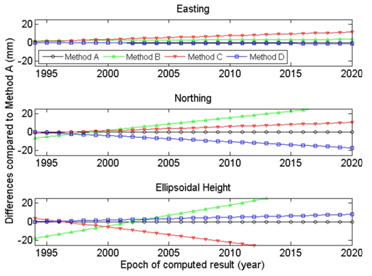
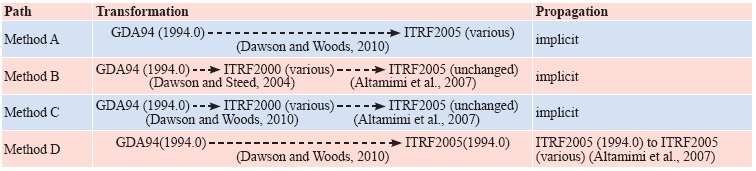
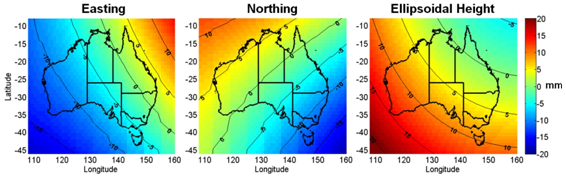
If you’ve ever had to put together a jigsaw puzzle of spatial data obtained from different jobs, by different methods, from different eras or from different organisations, then you know the importance of making sure all the jigsaw pieces come from the same box. That is, you’re working with all apples or all oranges. Stories abound of the errors that occur from mixing (i.e. ignoring) the datums in which data were observed, processed, archived or supplied to the next user. A lesser known issue of growing importance for users trying to squeeze all they can from new positioning techniques is how the transformation between datums was actually done. This applies to many users, whether they are using GNSS, LiDAR or imagery data to name just a few. Whilst national transformation parameters, endorsed software or the way you did it last time may appear the easiest and most obvious solution, there are many paths for data to travel between datums. Which one should you follow?

Now consider today’s spatial environment, with data gathering tools operating on a global scale, employing global datums. Couple that with a drive for new and improved datums that are being developed faster and faster, as more accurate tools make older datums obsolete or at least stale. There is no longer a 20-year gap between the release of improved datums, but rather a 5-year, 2-year or even faster (e.g. continuous for scientifi c users) re-defi nition. In addition, the position changes between datums are becoming smaller and are therefore harder to indentify. In the past, a 200-metre, 1-metre or 50-centimetre blunder was easy to detect. Now you’re trying to correct those last mismatches at the few-centimetre level that plague your data. Are these caused by ground movement, instrument error or simply by the ‘transformation path’ and the parameters chosen?

Obviously, before any datasets can be compared or combined, they must be brought together onto the same datum (Janssen, 2009). The practice of transforming from one datum to another is not diffi cult and the necessary parameters are available in many different software packages. However, with the increased number of datums comes an increased number of ways to transform between datums.

This paper demonstrates that differences of up to several centimetres in both horizontal and vertical coordinates can result from following different transformation paths. We suggest that some (but not all) users need to be careful of the methods employed. Additionally, the effect of the formal uncertainty in the transformation procedure on the estimated uncertainty of the output coordinates is often ignored, at the user’s own risk. If included, formal uncertainty could help solve any discrepancies right away. Using some Australian scenarios, we discuss these issues to give spatial professionals a better understanding of the effect transformations have on the quality of their data.

Datums commonly used in Australia

The current national horizontal coordinate datum in Australia is the Geocentric Datum of Australia 1994 (GDA94). Positions in GDA94 can be expressed in Cartesian coordinates (X,Y,Z), geographic coordinates (φ,λ,h), or projected (Map Grid of Australia, MGA94) coordinates as Easting, Northing and Height. Converting between coordinate systems (e.g. Cartesian to geographic) is mathematically exact and introduces no error. However, any organisation which has been gathering data for a prolonged period, or which makes use of data from other sources, will likely hold data in many different datums such as the Australian Geodetic Datum (AGD66 and AGD84), GDA94, the World Geodetic System (WGS84), various incarnations of the International Terrestrial Reference Frame (e.g. ITRF2000, ITRF2005, ITRF2008), and even historical datums superseded several decades ago.

Recall that different datums adopt different ellipsoidal coordinates for offi cial ‘datum’ stations and may be based on ellipsoids of different size, shape or orientation. In contrast to conversion, transforming between datums requires a model, which is not exact and subject to any uncertainty in the transformation parameters. Directly comparing coordinates without accounting for this change in datum can cause signifi cant errors. Similar effects can be caused by the transformation path selected and the transformation parameters chosen.

Complications arise because today’s datum of choice may well be a global (and therefore dynamic) datum such as the ITRF (Altamimi et al., 2011). In a dynamic datum, where coordinates change due to tectonic motion and/or ground distortions, it is important to note the instant in time (i.e. epoch) at which the position is valid. The latest scientifi cquality ITRF datums are not restricted to scientifi c users. Popular online GNSS processing services and commercial products commonly used in precision agriculture and GIS applications often provide positions in the latest ITRF. These positions are only valid at the epoch in which the data were gathered.

Since GDA94 was introduced in Australia, there have been several refi nements of the ITRF, each including the publication of new transformation parameters. As a result, there are many different combinations of transformation routines by which data can travel from GDA94 to a particular ITRF and vice versa. The assumption that the GDA94, ITRF and WGS84 datums are identical for most practical purposes is no longer valid. Modern positioning techniques can detect the small discrepancies between these common datums. Similarly, newer datums generally represent ‘only’ centimetre-level refi nements in datum defi nitions. However, ignoring these differences would introduce errors that may exceed the accuracy specifi cations required for a given application.

Static vs. dynamic datums

Australia (much unlike its neighbours New Zealand, Papua New Guinea and Indonesia) sits on a tectonic plate that has a high internal stability. Historically, we have therefore only employed (and enjoyed) a static datum where the coordinates of a ground mark do not change over time. As a result, the epoch at which the position or observation is determined is generally not recorded.

In a dynamic datum, the coordinates of a point continuously change as the underlying tectonic plate moves or deforms. The same ground mark will have continuously changing coordinates, but only one unique position per epoch. Therefore, both the datum and the epoch must be defi ned for all coordinates reported in a dynamic datum. The epoch should always be declared in decimal years in parentheses. For example, ITRF2005(2012.135) indicates a position in ITRF2005 valid at 12:00 UT on 19 February 2012. The decimal is calculated by day of year (50) minus one, plus time in the day (0.5 days), divided by the number of days in the year (366, remembering that 2012 is a leap year).

Transformation paths

In addition to having several valid datums to choose from, there are many different paths to take between these datums. Figure 1 illustrates the ‘landscape’ of current transformations relevant in the Australian context, showing possible paths between GDA94 (static national datum) and the three most recent realisations of ITRF (dynamic global datums). Here we only mention three distinct epochs because of their common usage, but any other epoch is equally valid. 1994.0 represents the epoch of the defi nition of GDA94. 2000.0 represents an epoch in which coordinates are often reported to allow direct comparisons at a common epoch. Finally, ‘current’ represents the date at which the data were observed.

Readily available online or downloadable tools can assist with current and historical transformations, as well as conversions between coordinate systems. However, without vigilance, it is easily possible that different software will employ different transformation paths or parameters to report the ‘same’ transformation (say,from GDA94 to ITRF2005). Current metadata records of existing data may be insuffi cient to make this distinction.

Figure 1: Landscape of current transformations available in the Australian context. Four different paths to travel from GDA94 to ITRF2005 (current) are highlighted and discussed later.

Transformation vs. propagation

Three distinct types of coordinate manipulation are demonstrated in Figure 1. In particular, the distinction is made between transformation and propagation. Transformation means coordinate values change due to a change in the datum origin, orientation and/or scale employed. Propagation means that coordinate values change over time due to some velocity (e.g. tectonic motion) of the mark within the same datum.

Moving from Left to Right (or vice versa) within Figure 1 represents a transformation, from datum to datum. Input and output coordinates are valid at the same epoch. For example, a position valid at 12:00 UT on 19 February 2012 in ITRF2005, i.e. ITRF2005(2012.135), can be transformed to one valid at 12:00 UT on 19 February 2012 in ITRF2008, i.e. ITRF2008(2012.135).

Moving from Top to Bottom (or vice versa) within Figure 1 represents the change in coordinates over time in the same dynamic datum. Here, the velocity of the mark is used to propagate the coordinates through time, within the same datum.

Diagonal movements within Figure 1 represent the special case of the transformation between a static datum (e.g. GDA94) and a dynamic datum (e.g. ITRF2005). This can be considered as transformation and propagation combined into the same set of parameters.

Transformation parameters

Transformation parameters that allow data to be transferred between datums are commonly supplied by national or international agencies. As new datums are defi ned (or refi ned) based on increased amounts of input data and improved processing techniques, new and better transformation parameters are published. However, there may be a signifi cant delay between their initial availability and eventual adoption in software via updates or patches.

The two most common transformation models are the 7- and 14-parameter similarity transformations. These are based on Cartesian coordinates (X,Y,Z). A similarity transformation retains the shape of the network during the transformation. Seven parameters define the relationship between the two datums at a certain point in time known as the reference epoch: three translations, three rotations, and one scale change. The additional seven parameters define the rate of change of these parameters. These extra parameters are required to modify the transformation parameters for use at epochs different to the reference epoch.

Comparison of transformation methods in Australia

As shown in Figure 1, there are many different paths that can be followed to transform data between GDA94 and the various realisations of ITRF. However, not all transformations have the same precision or accuracy. The most recently published transformations are assumed to be of greater quality, due to improved processing techniques and the larger number of observations used to compute the parameters.

We explored the differences between four of these potential paths (Table 1). Each one is a reasonable method to transform between GDA94 and ITRF2005, and may satisfy a contractor’s requirements for coordinates in a local datum using national parameters. Method A represents current best practice, following the most direct path using the most recently published parameters. Therefore we used Method A as ‘ground truth’. Until recently, no direct transformation was available between GDA94 and ITRF2005. Instead, a 2-step transformation was required (Method B). Method C also uses this 2-step transformation, but replaces the parameters for the GDA94-to-ITRF2000 transformation with those most recently published. Method D uses only the most recently published parameters, but shows an explicit combination of transformation and propagation.

Methods A and D use only regional transformations determined specifi cally for Australia (GDA94-to-ITRF). On the other hand, Methods B and C also use global (ITRF-to-ITRF) transformations. Transformations between global datums require generalisations (at a global scale) of complex tectonic motion and can be less certain, especially when comparing data from different epochs.

The current datums used in Australia are expected to be in operation for at least another fi ve years. So we investigated the behaviour of the four transformation paths for epochs ranging from 1994.0 (reference epoch of GDA94) to 2020.0. For a given position in Sydney, we revealed signifi cant differences for those transformations that proceed in two steps via the now outdated ITRF2000 (Methods B and C). These differences exceed 20 millimetres in height (by 2010.0) and 30 millimetres in Northing (by 2020.0). Moreover, Methods B and C diverge from each other by several centimetres in height (Figure 2). Any software not updated recently may still be using these paths.

Methods A and D represent different techniques (transformation only vs. transformation and explicit propagation). Both employ only regional transformation parameters (GDA94-to-ITRF2005), in contrast to Methods B and C which also employ global (ITRF2000-to-ITRF2005) transformation parameters. Method D yields results that are most similar to Method A with differences in all coordinate components limited to less than 20 millimetres, even up to epoch 2020.0.

Figure 2: Difference in output coordinates after transformation of a point in Sydney by several methods
(compared to Method A) from GDA94 to ITRF2005 at various epochs between 1994.0 and 2020.0.

When performing the same comparison at locations across Australia, it quickly became clear that the differences between the methods are spatially dependent. This occurs because of the complex combination of translation, rotation, scaling and tectonic plate models. As an example, Figure 3 illustrates these differences between the most similar methods (A and D) across Australia, computed on a 1-degree grid of latitude and longitude over the area shown.

Error propagation during the transformation

Obviously the quality of the input coordinates will have a major effect on the quality of the output coordinates after the transformation (rubbish-in-rubbishout principle). However, the effect of the transformation procedure itself on the estimated uncertainty of the output coordinates is often not considered, nor output and rarely archived. Although an estimate of the quality of transformation parameters is usually published, transformation software generally

Table 1: Four different paths of transformation from GDA94 to ITRF 2005. These paths are also visualised in Figure 1.

Figure 3: Easting, Northing and Ellipsoidal Height differences in millimetres

(Method D minus Method A) at epoch 2010.0 across Australia. supplies only coordinate values (and not their quality) as output. This leads to the following question: What is the contribution of the transformation on the uncertainty of the output coordinates? Assuming a perfectly known input position, we can compute an example of how much formal uncertainty is inherent in a modern transformation.

We found that the most recent GDA94- to-ITRF2005 transformation (Method A) nominally contributes about 5-10 millimetres to the uncertainty of each coordinate component for an epoch between 2010.0 and 2020.0. Understandably this contribution steadily increases when the specifi ed epoch is further away from the reference epoch (in this case 1994.0), due to the extra uncertainty of the seven rate parameters. In contrast, the transformation between GDA94 and the most recent ITRF2008 is known with more certainty (due to improvements in ITRF2008 over ITRF2005) and only contributes about 2-4 millimetres in the same time span (Haasdyk and Janssen, 2011).

Importance of transformation metadata

Data previously transformed may have metadata giving details of the datum in which the dataset was collected, and of datum(s) to which it has been transformed. However, the method or path of transformation may well be lost or disregarded. In order to clearly identify what has happened to a particular dataset and help avoid the issues outlined in this paper, metadata should include the following information in regards to transformations:
• Complete transformation path (including propagation if employed) from Datum 1 to Datum 2.
• Transformation parameters used and how they were computed, or citation of reference document.
• Epoch(s) at which the transformation parameters are valid.
• Sign convention used for the parameters (e.g. positive for anti-clockwise rotation of the coordinate axis).
• If an explicit propagation is applied, site velocities used and their source.
• If possible, quality (uncertainty) of the transformed coordinates and of the transformation parameters.

Conclusion

Recently a number of new transformation parameters have been published, allowing users to transform data between the current (static) national Australian datum (GDA94) and the latest global (dynamic) ITRF datums. This has created a problem of choice because there are many different paths of transformation by which data can travel between these datums.

We have demonstrated that differences of up to a few centimetres in each coordinate component can occur depending on the choice of the transformation method applied between GDA94 and ITRF2005. For all transformations, the expected quality of output coordinates degrades with greater time separation from the transformation’s reference epoch. These differences can be disregarded for many navigation, mapping and GIS purposes. However, users requiring coordinate qualities at the centimetre-level need to be aware of the transformation methods employed by their software. This includes the transformation paths previously followed for existing data and is particularly important when mixing data from different periods and sources.

All users need to be increasingly careful when using multiple datums and transforming between them. The highest and most consistent coordinate quality is obtained by following the most direct transformation path and applying the latest transformation parameters to the original untransformed data (i.e. Method A). Metadata for transformed data should include information on the specifi c transformation path followed with reference to the transformation parameters, their source, and the epoch(s) used in the transformation.

References

Altamimi Z, Collilieux X, Legrand J, Garayt B, Boucher C (2007) ITRF2005: A new release of the International Terrestrial Reference Frame based on time series of station positions and Earth Orientation Parameters, Journal of Geophysical Research 112: B09401, doi:10.1029/2007JB004949.
Altamimi Z, Collilieux X, Métivier L (2011) ITRF2008: An improved solution of the International Terrestrial Reference Frame, Journal of Geodesy 85(8): 457-473.
Dawson J, Steed J (2004) International Terrestrial Reference Frame (ITRF) to GDA94 coordinate transformations, http://www.ga.gov.au/image_cache/ GA3795.pdf (accessed Jan 2012).
Dawson J, Woods A (2010) ITRF to GDA94 coordinate transformations, Journal of Applied Geodesy 4(4): 189-199.
Haasdyk J, Janssen V (2011) The many paths to a common ground: A comparison of transformations between GDA94 and ITRF, Proc. IGNSS2011 Symposium, 15- 17 November, Sydney, Australia, 16pp. Janssen V (2009) Understanding coordinate reference systems, datums and transformations, International Journal of Geoinformatics 5(4): 41-53.