| Geodesy | |
C++ programming for cartography and geodesy students
The issues of development and use of a training course on C ++ programming under the conditions of teaching of students in two academic subjects of general geodesy and programming are considered. Recommendations for teaching students on the basis of the introductory course of “C++ programming for cartographers and surveyors” and ways of solving the related tasks using modern information technologies are given |
 |
|
Introduction
At the Moscow University of Geodesy and Cartography, junior students are taught C++ programming according to a new training course tailored specifically for future cartographers and surveyors. The development of this training course took over 10 years. In the process of developing the training course, specific geodetic and cartographic tasks were selected. Later to solve those tasks already developed algorithms were implemented. The tasks are required to be simple and comprehensible enough so undergraduate students could understand them. We chose real practical tasks, which any cartographer and any surveyor often deal with in the performance of his professional duties.
Based on the selected problems and algorithms to solve them, C++ programs were developed. The sequence of computer programs for study was also specified. The developed sequence of programs as far as possible corresponds to the range of issues studied in the course of general geodesy and cartography. Thus, students start programming classes being acquainted with the geodetic content of programs and having deep understanding of them, due to the fact that they have already studied those issues during the general geodesy course.
Difficulties could appear in process of linking courses of general geodesy and programming studied at once. As it is known in the course of geodesy, the study of the subject begins with such issues as: the shape and size of the Earth, coordinate systems, orientation of lines, the concepts of a map and a plan. This is followed by the theory of errors in geodetic measurements, and then issues of measuring distances and angles on the ground are considered. After that students start working with measuring instruments (level, theodolite) and performing topographic surveys. Therefore, in the same sequence, students are encouraged to work with training computer programs, and they are to develop their own versions of the programs.
On the other hand, learning C++ programming is also based on a certain order of training content presentation [1, 2]. At the beginning of the course, basic data types are considered and then control instructions (conditionals and loops) are to be studied. This is usually followed by arrays and strings, then pointers and references. The structured programming section ends with the study of functions. The C++ object-oriented programming part consists of introduction to classes, operator overloading, inheritance, and polymorphism. Currently, a fairly complete set of curricula which covers all the above sections of the C++ programming language has been developed. All computer programs contain geodetic and cartographic content and have been repeatedly tested during the educational process.
We emphasize that the analysis of training computer programs and programming tasks are offered to students after they have become acquainted with the solutions of those problems in the course of geodesy. At the beginning of the training course, students are not offered programs containing issues of usage of the geodetic instruments or features of topographic survey. Programs related to those issues are considered generally at the end of the training course. Of course, there are no hard restrictions, but changing the sequence of programs would require additional efforts from a teacher of the computer science to give students geodetic grounding of the proposed tasks.
The process of teaching students in practical usually involves running the program on a personal computer and then analyzing the instructions of the program. For this purpose, an interactive electronic board is used. Typically, the code of the program is presented on the blackboard. The students should modify the given code, correct syntax or logical errors, and then compile it and run. To check the results of the program performance, a test case is used to quickly determine whether a student has coped with the task or not. At the beginning of the course, rather simple geodetic tasks are used. For example, one needs to calculate the distance between points on the map or the height of a point, or the incline of the slope line, etc. If the obtained and control results match, the student goes to the second stage of the test. To develop C++ programming skills, students perform analysis of the program code in speech. Indeed, at the beginning the programs contain only a few lines, then the number of lines of code increases. Verbal analysis of the code means explaining each instruction in the code and answering questions in regard to the essence and functioning of each line of instruction. For all computer programs, a reference source that explains the purpose of each program instruction was developed.
During the pedagogical experiment, various methods of teaching students and their influence on the retention of training content were investigated. For this purpose, observations of the results of learning process were made. The process was centered on the task to create training programs in “two hands”, when two students were put at a personal computer. This organization of programmers’ workflow is used in Scrum flexible programming methodology [3]. It is believed that pair programming contributes to concentration, simplifies the search for errors, stimulates brainstorming and helps participants learn all the features of the program code. However, as experience in the learning process has shown, putting two students at one computer led to conflicting results. Sometimes the effectiveness of the joint work increased and an interest in achieving high results and mutual assistance was observed. Nevertheless, there were also opposite cases, when two students at one computer worked ineffectively and the results turned out to be worse than in case of their individual work. In other cases, loss of the efficiency in pair programming was not observed. Hence, it is to be concluded that we should be leery of implantation of pair programming in the educational process. The task is being completed mostly by the most active student, while his partner is just an observer. In this case, the best option is to fit students to the scheme “one student — one computer”. Then, the very fact that it is not possible to take part in programming via observing somebody’s work leads to the correct prioritization and, as a rule, ends with the timely completion of the educational task. The student, being alone with the PC, feels that at the end of the lesson he will personally report on the work done. This burden of responsibility keeps students on their toes and as a result the work is done on time.
When developing training computer programs for cartographers and surveyors, the question regarding the method of calculating values was decided. Typically, survey results are double checked. There is even such a special term as “calculation in two hands”. In other words, it is control of the performance of calculations. For example, to determine the rectangular coordinates of a point on a topographic map, it is enough to measure two distances, from the desired point to the south line of the coordinate grid and from the same point to the west line coordinate grid and perform calculations. However, for control, the distances from a point to the north and east grid lines are also measured. As a result, two coordinate values X and Y are obtained. Average values are taken for the final coordinates of the desired point.
There are many similar calculation schemes including control in geodetic and cartographic tasks. The use of detailed computational schemes adopted in geodetic manuals when developing programs is a subject to investigation. Geodetic computational schemes including control prevent arithmetic errors in calculations which the computer does not commit anyway. The question is whether it is necessary to include such schemes in the algorithms of training computer programs for processing geodetic and cartographic data. It might be easier to use a reduced algorithm without additional control and then implement this algorithm in a computer program.
The answer to the questions largely depends on the computational scheme used. If the computational scheme is aimed at carrying out additional measurements, then it is likely that such control should be taken into account when algorithmizing the problem and drawing up a program. Control measurement reduces the risk of using fallible data. On the other hand, if the calculation scheme provides only a recalculation of the desired values, and nothing more, then such a check will be unnecessary. A computer, unlike a person, does not make arithmetic errors. Unlike arithmetic errors, errors in input data occur. Therefore, if data input in the program is provided, for example, from the keyboard, it is probably necessary to protect the program from receiving the fallible data. Nevertheless, if data input into the program is not provided (since they are written in the program text as constant values) the use of a double computational check scheme is unjustified.
It could be proven by considering a more detailed algorithm for determination of the rectangular coordinates of a point. This algorithm is used when working with an old and wrinkled topographic map. To simplify the analysis, consider the calculation of only the X coordinate. The algorithm for calculating the increment of the X coordinate is presented below by formulae (1, 2, 3, 4):
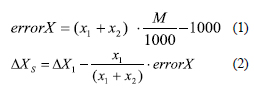
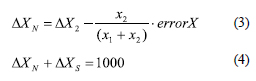
where x1 + x2 is the sum of the lengths of perpendiculars to opposite sides of the map grid square (mm), M is the denominator of the map scale; ΔX1 and ΔX2 are the increments of coordinates of a point from the south and north sides of the grid square; ΔXN and ΔXS are the total increments of coordinates of a point; errorX is the abscissa error of the required point.
In the above given algorithm, the error in the graphical determination of the abscissa is first calculated by the formula (1), if this error is acceptable, then the increments of the X coordinate from the north and south sides of the kilometer grid are calculated using formulae (2 and 3). Next, the calculations are monitored using formula (4).
Since arithmetic errors in calculating the increments of coordinates on a computer are not possible, the control of the sum of increments according to formula (4) is clearly unnecessary. Moreover, the control calculation by formula (3) in the program would not increase the accuracy of determining the coordinates of the desired point.
Therefore, elimination of this check makes the curriculum simpler and easier to read. Thus, in those cases when the data entered from the keyboard into the program are to be processed, a computational scheme with control should be used. In other cases, controlled computational schemes are above measure. To simplify the computational algorithms in a number of programs, the data were embedded in the program code. In these cases, abbreviated computational schemes were used without repeating of calculations.
Next, we consider a training computer program designed for students of geodesy and cartography who also study C++. The program demonstrates the use of the do_while loop statement. The problem of monitoring the computation results in the developed program is solved by restarting the program and re-entering the initial data. This monitoring method is also widely used in the processing of geodetic measurements and can be applied when working with a computer program. Such a monitoring scheme simplifies the program code and, as a consequence, makes it comprehensible for beginner students of programming. This is the main advantage of the scheme.
Materials and methods
To accomplish the task, the Microsoft Windows 10 operating system was used on a personal computer. The open source programming environment Code::Blocks and the GCC C++ compiler were also in use while performing the work.
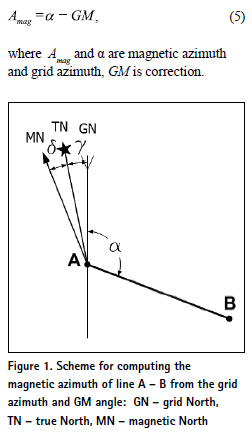
Let us dwell on the geodetic formulation of the problem. Let it be required to calculate the magnetic azimuth of the direction for a given grid azimuth of the A – B direction and the magnitude of the GM angle. As it is known [4], the following formula is used to calculate the magnetic azimuth of the А –. direction:
The GM angle is found as the difference between the declination of the magnetic needle δ and the magnitude of the convergence of the meridians γ.
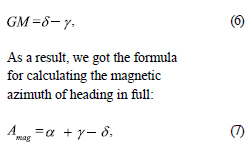
In the above given formula, both the declination of the magnetic needle and the convergence of the meridians can have a “+” sign, or a “–” sign. To use the correct signs, diagrams are often used. Please, consider an example in Figure 1. This figure corresponds to an example 1 given in table 1.

Discussion of the results
The program below performs arithmetic operations on angles without converting them to degrees with a fractional part. Therefore, there is no need to convert the values of degrees with a fractional part into degrees and minutes. To perform arithmetic operations on angles, degrees are converted to minutes, and then the program performs the calculations. Let us take a closer look at the code of the program.
This program is intended to illustrate the training content of the 5th lecture “C++ for cartographers and surveyors” [5]. In this lecture, students are introduced to programming concepts such as loops and learn to compose programs using these constructs. The lecture describes how to repeat one or more instructions a certain number of times or until a certain condition is true. The following loops: for, while and do-while are used. The operations performed during the execution of statements of the for-loop are analyzed step by step; the schemes of the loop operation with the counter increment and counter decrement are presented. The features of while and dowhile of infinite loops are considered. It must be noted that in some cases usage of such loops should be avoided, however they fit perfectly to solve particular tasks. Using specific examples from geodesy and cartography, the difference between loops are shown. Corresponded types of tasks for each type of loop are described. Making students familiar with loop instructions usually takes place at the initial stage of programming course. Acquirement of skills in usage of the loop instructions is an important milestone in mastering the basics of programming.
Each of the curricula used in the “C++ for Cartographers and Surveyors” course has explanatory text intended for students to learn what a computer program does and how it works. The following is an explanatory reference for the program under study.
In lines 07 – 08, variables are declared. The integer variables degrees and minutes are used many times, first to define the bearing grid angle, then for the convergence of the meridians, and finally for the declination of the magnetic needle. The main program instructions are in the body of the do_while loop in lines 11 – 39. In line 13, the value of the grid azimuth of the A – B direction is input from the keyboard. The received data are converted into arc minutes. Further, in line 17, the value of the convergence of meridians and the value of declination of the magnetic needle in line 21 are also input.
In the program, when it comes to negative angular values, for example, the value of the convergence angle of meridians or the value of declination of the magnetic needle, the “minus” sign is to be entered twice: first for degrees and then for minutes. If the declination of the magnetic needle is –8° 30′, this value is entered as –8 followed by a space and –30. In line 25, the G-M angle value is calculated according to the formula (6), in line 27, the magnetic bearing of heading according to the formula (5). In the English-language geodetic literature, to define the grid-magnetic angle the G-M angle notation. The magnetic azimuth of the A – B direction is also expressed in arc minutes. After computing the magnetic azimuth of the heading in lines 29 and 30, it is to be checked if the obtained magnetic azimuth lies in the range of 0° to 360° (angular values are in minutes).
Line 29 uses the abbreviated form of the if statement and checks whether the resulting azimuth is greater than 360°. If the expression magneticAzimuth > = 360 * 60′ is true, then the value of the magnetic azimuth decreases by 360 * 60′. It uses the “compound assignment operator with subtraction”: magneticAzimuth –= 360 * 60′. Line 30 uses the abbreviated form of the if-statement and checks whether the resulting azimuth is less than 0°. If the expression magneticAzimuth < 0 is true, then the value of the magnetic azimuth increases by 360 * 60′. It uses the “compound assignment operator with addition”: magneticAzimuth + = 360 * 60′.
In lines 32 – 33, a whole fraction of degrees and minutes are calculated using the value of the magnetic azimuth. The results are displayed on the screen. The screen output of degrees and minutes is performed in the format accepted in geodesy, for example, an angle equal to 45° 6′ will be written as 45° 06′. To do this, line 34 uses the setw (2) and setw (2) output modifiers, and line 10 uses the cout.fill (‘0’) placeholder. Then the program displays the question “Do you want to proceed?” If the letters “Y” or “y” (short for “Yes”) are input, the do_while loop keeps working. The user can compute the next magnetic azimuth for the new initial data. If any other letter is input by the user, the do_while loop stops its work. This is where the program stops.
Let us make a final remark. Using angular minutes instead of degrees with a fractional part allows performing arithmetic operations (such as division or modulus division) using the “/” or “%” operators and not lose 1′ while performing the computations. If degrees with a fractional part are used, then when converting degrees to minutes in reverse, a minute could be lost. The standard math function round was not used deliberately in the program, as it is studied in the Functions section.
Testing of the program
Let us test the program. After compiling and running the program, enter the initial values from the first three columns of Table 1. The results of the program calculation are presented in the column “Magnetic bearing”.
Conclusions
At the Moscow University of Geodesy and Cartography, a new training course “C++ for cartographers and surveyors” is used to educate students. The issues of the development and use of a training course under the conditions of teaching of students in two academic subjects of general geodesy and programming are considered. Recommendations for teaching students on the basis of the course of “C++ programming for cartographers and surveyors” and ways of solving the related tasks using modern information technologies are given. A computer training program to be used as a training content in lectures, seminars and for homework has been developed. The program computes the magnetic azimuth of heading using the grid azimuth of the direction, the Gaussian convergence of the meridians and the magnetic declination. The program can be used as a training content at a programming course to illustrate loop instructions. An example of reference information for self-study, which describes in detail the program code and explains the purpose of the instructions used, is presented.
References
1. Podbelskiy V.V. (2003) C++ language. Finance and Statistics. Moscow, Russia.
2. Siddhartha Rao (2012) SAMS Teach Yourself C++ in one hour a day. SAMS, USA.
3. Stellman A., Greene J. (2017) Head First Agile. O’Reilly, USA.
4. Poklad G.G., Gridnev S.P. ( 2007 ) Geodesy: a textbook for universities. Academic Project. Moscow, Russia.
5. Zablotskii V.R., (2017) Teaching C++ programming language at Moscow State University of Geodesy and Cartography through the geodesic problems and programs. Proc. 17th Geoconference, SGEM-2017, Bulgaria. https://doi.org/10.5593/ sgem2017/21/S07.082.













 (1 votes, average: 4.00 out of 5)
(1 votes, average: 4.00 out of 5)





Leave your response!