| GNSS | |
Assessment of GNSS real time kinematic relative positioning accuracy based on NTRIP data transmitted by the Brazilian CORS Network (RBMC-IP)
This work aims to assess real time kinematic relative positioning accuracy based on the Brazilian CORS Network (RBMC-IP). For this, RTKLIB free software was used with an unconventional technique to obtain the observations |
 |
|
 |
|
In the past decades, Global Navigation Satellite Systems (GNSS) have revolutionized positioning and navigation activities. Currently, in addition to GPS and GLONASS, developed respectively by the US and Russia (formerly USSR) are fully operational, Galileo, being implemented by the European Union, and BeiDou, by China, expect to reach full operational capabilities around 2020 (FORTES, 2016).
GNSS positioning encompasses several types of users ranging from the average user to professionals and scientists who require a higher level of positioning accuracy, whether static or kinematic. The demand for better precision in real time motivated the development of the relative positioning techniques Real Time Kinematic (RTK) and Differential GNSS (DGNSS), for which there is a need for real-time transmission of observations or corrections to these observations from a known base station to the remote station, whose coordinates are to be determined. Initially, this transmission between the two stations (base and remote) was predominantly established via radio. Other implementations, especially those provided by companies that use networked solutions based on more than one reference station, use communication satellite data transmission, which substantially increases the solution cost.
Due to the possibility of data transmission via the Internet, existing reach restrictions when using radio link have been overcome, allowing a greater efficiency in surveys where this technique is used. The user can access the Internet using a smartphone and obtain data from one or more base stations provided by a NTRIP Caster server, for example (MONICO, 2008). With the permanent expansion and modernization of the Brazilian Network for Continuous Monitoring of GNSS (RBMC), implemented in Brazil by the Brazilian Institute of Geography and Statistics (IBGE) in partnership with several institutions in the country, data collected at a rate of 1 second in 104 out of 144 stations that currently compose the network are transmitted in real time over the Internet using the Networked Transport of RTCM via Internet Protocol (NTRIP – BKG, 2017a). These 104 stations constitute what is known as the RBMC-IP network (IBGE, 2018).
Data transmission is performed as follows: a GNSS receiver from a reference station continuously sends messages in the RTCM format to a NTRIP Caster server located at IBGE headquarters. A user with a client application, such as BNC (BKG NTRIP Client – BKG, 2017b) or RTKLIB (TAKASU, 2013), and with an Internet connection connects to the IBGE server and selects RBMC-IP station (s) whose data or differential corrections he/ she wishes to receive. These are received by a computer connected to the user’s receiver through a serial or USB port and by this way the corrected positions are obtained (IBGE, 2018). Thus, any user in Brazil with Internet access at a remote station can receive real time data from the nearest RBMC station and perform an RTK positioning, using carrier phase observations, or DGNSS, using pseudoranges. The use of the RBMC-IP infrastructure allows the user to reduce costs, as there is no need to have a pair of receivers to occupy both base and remote stations, besides allowing the establishment of baselines longer than those obtained previously with radios.
DGPS and DGNSS
The DGPS (Differential GPS) technique was developed with the objective of reducing the effects of selective availability imposed on GPS (MONICO, 2008). As this effect greatly depreciated the quality of the coordinates of the satellites and/or the stability of their clocks, compromising the precision of the coordinates obtained, it was necessary to develop a way to increase the accuracy of the determination.
The method is based on the use of a receiver set up at a known coordinate station, tracking the visible satellites, while another receiver occupies the places of interest. The concept is all based on the pseudorange corrections calculated at the reference station and transmitted to the rover station.
This method can provide accuracy in the order of 0.5 to 3m (depending on the length of the baseline), having the ability to perform real-time positioning, although it is also possible to perform post-processing (MONICO, 2008). As with relative positioning techniques, the DGPS technique is directly affected by the baseline length, degrading its accuracy as it increases (FORTES, 2016).
The emergence of other GNSS systems besides GPS improved the quality of the positioning, due to the fact that more constellations of satellites are available for tracking, providing more observations, which contributes to the improvement of the geometry of the solution (FERREIRA and FORTES, 2016). Thus the DGNSS technique is based on the same concept of the DGPS technique, but using other constellations besides GPS to perform the positioning.
Real-time kinematic (RTK) relative positioning
The real-time kinematic (RTK) relative positioning technique is based on the use of carrier phase – and code (pseudorange) – observations measured from the signals transmitted by GNSS satellites. Analogously to DGNSS, it is also based on the transmission of data collected at a reference station (base) to the rover station through a link that can employ modem using radio waves, or through GSM technology or any other system of communication (MONICO, 2008). The receiver of the rover station must usually have appropriate software for performing the data processing in real time. The purpose of the RTK technique is to obtain coordinates with good accuracy (i.e., centimeter) instantly, without the need for post-processing of data.
According to Seeber (2003), RTK technology is based on the following characteristics:
• Real-time transmission of carrier phase and pseudorange data from the base station to the rover station or corrections thereto;
• Resolution of the ambiguities as integers almost in real time (on the way or on the fly), allowing the accuracy to reach the centimetric level;
• Reliable determination of the baseline vector in real time or near real time.
The RTK technique has great advantages over conventional topography techniques because it has good real-time precision and is highly productive. However, there are limitations when using the more traditional methodology of VHF/UHF radio waves for communication between receivers. These limitations occur in heavily obstructed environments (vegetation and buildings), which reduces the reach of the radio link that transmits differential corrections.
On the other hand, the significant technological advance in the last decades, especially in the use of the Internet in mobile systems, made possible a great transformation in RTK applications. Due to the possibility of data transmission via the Internet, the restrictions that exist when using the radio link are overcome, making possible a greater efficiency in the surveys where this technique is used. The user can access the Internet using a smartphone and obtain data from a NTRIP Caster server, for example (MONICO, 2008).
Because of its real-time capabilities, this technique has a variety of applications, among which it is worth mentioning: precision agriculture, mining, construction, topography, navigation, among others. Therefore, this technique is widely used, being one of the most advanced in the current state of the art of GNSS positioning.
Ambiguity vector solution
When discussing relative positioning, one issue that is extremely important is the solution of the vector of ambiguities. For real-time kinematic applications, it is of fundamental importance to quickly resolve the ambiguities, allowing the estimation of the whole numbers of cycles.
The effects of ionospheric and tropospheric refraction, multipath and other unmodeled errors, as well as the geometry and number of satellites, affect the solution of ambiguities. Another important aspect is the duration of the observation session. The contribution of carrier phase observations in this process is a function of time, being directly correlated to the satellites movement (MONICO, 2008).
In general, the solution of the vector of ambiguities is classified into two types: floating solution (Float) and fixed solution (Fixed). In the first one the ambiguities are determined in the least squares adjustment or in the Kalman Filter as Real numbers (л). The fixed solution is obtained by determining the ambiguities of the satellites as integer values, obtaining, in this way, high precision (FORTES, 2016).
Study area
This project was carried out using RBMC-IP stations described in Table 1.
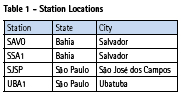
The two baselines have the following lengths: 10 km for SAVO-SSA1 and 82 km for SJSP-UBA1.
Equipment and programs used
The equipment used in RTK and DGNSS techniques generally comes complete in terms of hardware and software for this purpose. In this work, however, the conventional configuration used in this method was not used, where the rover receiver receives the data from the reference station by means of radio or other form of communication and the positioning solution is usually generated at that station.
All the surveys were carried out in this work using data streams transmitted by the those four RBMC-IP stations and received via the Internet by the RTKLIB software. Version 2.4.2_p12 of this software was installed and operated on a notebook with Windows operating system with broadband Internet connection, through which all kinematic processing was performed in real time, reproducing the type of survey that is performed in a conventional manner.
RTKLIB
RTKLIB software is a free, open source software package for real-time or postprocessed GNSS positioning developed by Tomoji Takasu. This package consists of several programs and a library that can be used in the development of programs for processing GNSS data (TAKASU, 2013). For this research, the RTKNAVI program, the RTKLIB software package component responsible for real-time processing, was used.
Methodology
As previously indicated, in this work two stations of the RBMC-IP were considered, one as a rover station and the other as a base station, both transmitting over the Internet the data streams that were received and processed in the kinematic mode by RTKNAVI. By this way it was possible to compare the coordinates obtained for the station considered rover and those of reference, allowing the determination of the positioning accuracy.
In RTKNAVI, it was necessary to select the stations data streams, frequency and the positioning technique to be used. For other options, such as a priori errors of phase and code observations, etc., the default values were not changed to evaluate the quality of the results that would be obtained by the beginning user.
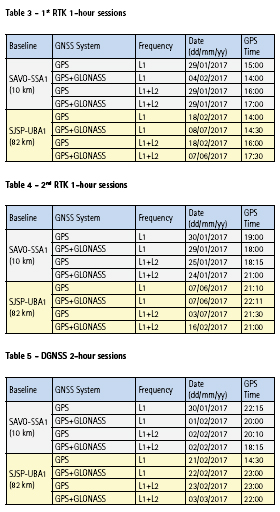
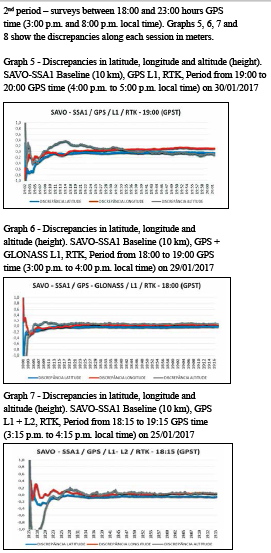
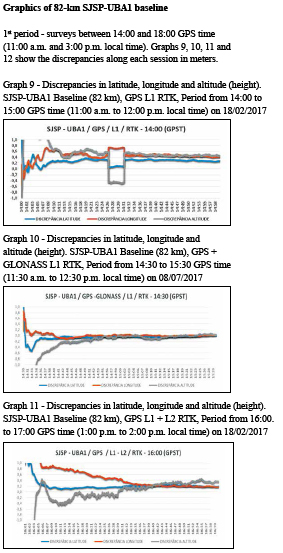
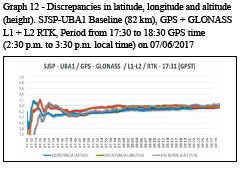
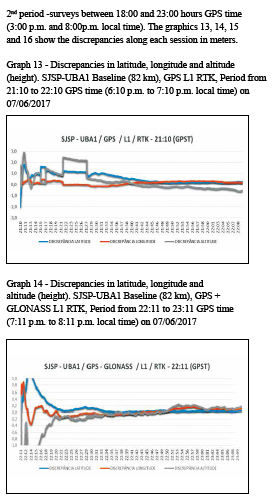
In this research, the two baselines used were processed totalizing 24 observation sessions, divided as follows: two RTK surveys in two observation periods, with sessions between 14:00 and 18:00 (11:00 a.m. 15:00) and between 18:00 and 23:00 (15:00 and 20:00) hours, GPS time (local time), with an hour each, to evaluate the quality of the positioning under various ionospheric conditions; additionally, a DGNSS survey with a twohour duration between 14:00 and 01:00 (11:00 and 22:00) hours, GPS time (local time). All solutions were obtained in kinematic mode.
For each baseline, the variations of GNSS systems and frequencies were used for both RTK and the DGNSS techniques, as shown in table 2.
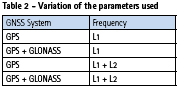
Figure 1 shows the set up used in this the work. Using two RBMC-IP stations simultaneously transmitting real-time data streams processed by RTKLIB RTKNAVI program, 16 RTK solutions and 8 DGNSS solutions were obtained in total for the two baselines, using the options listed in table 2.
In addition to the parameters mentioned above, the following input data were also provided to RTKNAVI: the antenna height and type for both the rover and the reference stations; reference coordinates of the base station; and the the phase center variation values of satellite and receiver antennas obtained from IGS, for their correction in the processing.
For dual-frequency positioning, the “IONO-FREE” option was used to eliminate the first order effects caused by the ionosphere; and for all processing options the “SAASTAMOINEN” option was used for the tropospheric corrections. The RTCM3EPH broadcast ephemeris stream made available by IBGE Caster was also used, as the stations were not transmitting the RTCM messages with this type of information.
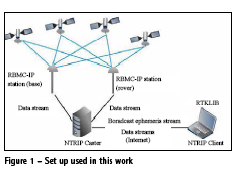
After the configuration of RTKNAVI, the RTK or DGNSS positioning processing was started in real time. The program interface, shown in figure 2, provides some information to the user, such as three-dimensional coordinates of the rover station, the time difference between rover and base stations in seconds (age) and ratio of the sum of the square of the solution residuals using the second best integer ambiguity vector and the best vector (ratio), with the latter arameter, also configurable in RTKNAVI, used as a criterion for accepting the integer ambiguities solution (usually, when greater than 3) (FORTES, 2016). In this type of processing, RTKNAVI may calculate one of the following types of solution: SINGLE (single point positioning), FLOAT (RTK without fixing integer ambiguities), FIX (RTK with ambiguities fixed to integers) and DGPS (DGNSS).
The program saves the coordinates of the rover station at each observation epoch (in this case, every 1 second) in a text file, thus allowing calculations and analysis of the quality of the results.
Calculations
In order to perform the calculations, the parameters of the GRS80 ellipsoid were adopted, with a equatorial radius (a)=6378137 meters and flattening (f)=1/298.257222101.
From these parameters were calculated the square of the first eccentricity (e2) (equation 1), radii of curvature in the prime vertical (N) (equation 2) and in the meridian (M) (equation 3):


where:
RMS is Root mean square of each solution.
n is number of epochs in each solution obtained in kinematic mode.
Results
The graphs of the coordinate discrepancies, convergence time and RMS obtained in each positioning solutions using RTKNAVI are presented in the following section.
Graphics
In this section the graphs containing the discrepancies between the coordinates of the rover station determined by RTKNAVI and the known coordinates of that station for each session listed in tables 3, 4 and 5 are shown.
RTK graphics
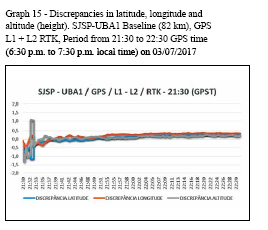
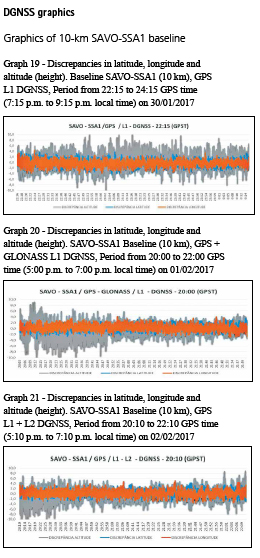
As described earlier, the RTK sessions were performed in two periods of one hour each.
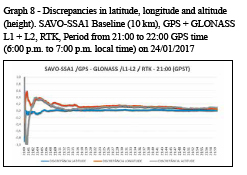
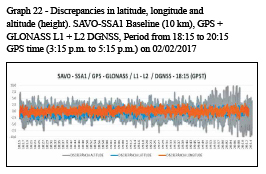
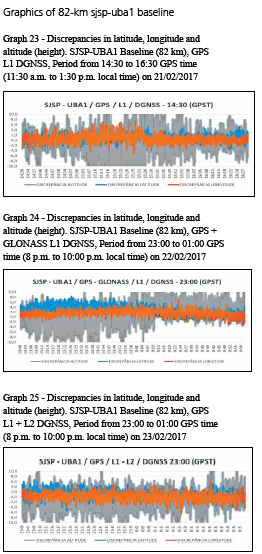
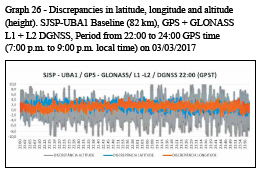
All discrepancies are expressed in meters and time is referred to GPS time (GPST), which is requivalent to local time +3h.
All surveys were performed in kinematic mode and are referenced to SIRGAS2000 at 2000.4 reference epoch.
Graphics of 10-km SAVO-SSA1 baseline
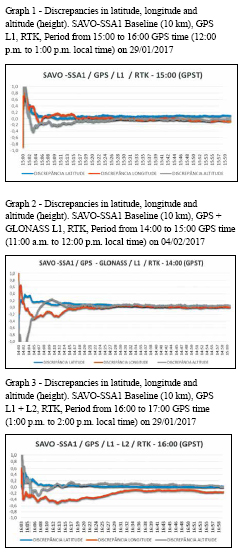
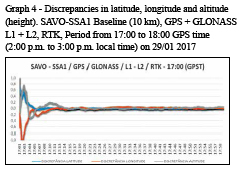
1st period – surveys between 14:00 and 18:00 hours GPS time (11:00 a.m. and 3:00 p.m. local time). Graphs 1, 2, 3 and 4 show the discrepancies along each session in meters.
Estimated convergence time
The approximate convergence time of the ambiguities and, consequently, of the coordinates, was extracted in each RTK solution from the visual analysis of the graphs of discrepancies shown previously, considering the epochs in which the discrepancies approached zero.
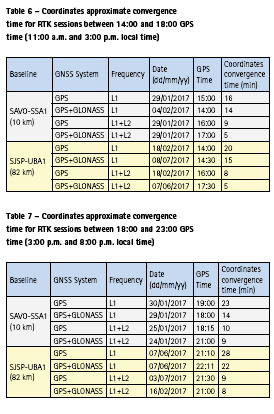
In Tables 6 and 7, it can be seen that the approximate convergence time of the ambiguities varies from 5 to 28 minutes.
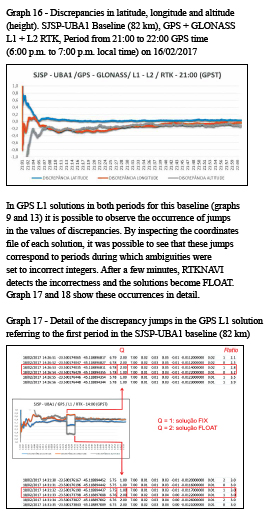
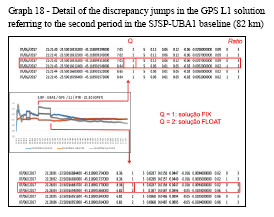
The convergence time was of fundamental importance for the calculation of the RMS values that are shown in section 9.3, since its calculation took into account only the epochs after the convergence time of the ambiguities. In addition, the periods corresponding to the discrepancy jumps in graphs 17 and 18 were excluded so that they did not contaminate the RMS values.
Obviously there is no calculation of convergence time for DGNSS surveys, since pseudorange observations are not ambiguous.
Root Mean Square (RMS) values
According to MACHADO (2008), RMS indicates the absolute accuracy because it does not use the average in its calculation, resulting in the absolute error in relation to the reference value. In this section, RMS values are presented through bar graphs to clearly expose the accuracy comparisons between each positioning solution.
Figures 3, 4, 5 show the calculated RMS values (in meters) for latitude, longitude and altitude (height), respectively, for RTK sessions from 14:00 to 18:00 GPS time (11:00 a.m. to 3 p.m. local time).
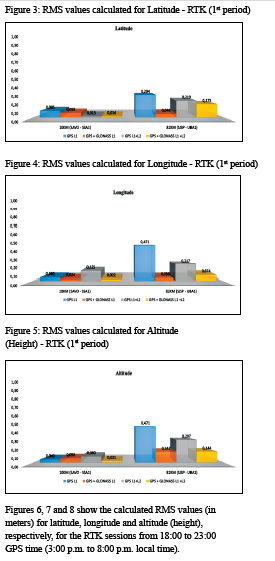
Conclusions
In this work, an unconventional real-time relative positioning technique was applied, using only data streams transmitted by RBMC-IP stations to evaluate the quality of RTK and DGNSS positioning based on data transmitted over the Internet. Therefore, this is a less favorable case than that which can be implemented in practice, using the data stream of an RBMCIP station as a reference for the positioning of a GNSS antenna whose receiver is connected by cable to a computer. The fact that all data used in the experiments (i.e., observations collected by both stations defining each baseline, in addition to the broadcast ephemeris) were accessed in real time through the Internet possibly introduced additional difficulties associated with connection stability that are not present in the real context.
With the exceptions mentioned in the previous paragraph, it should be noted that, in a general way, the performed surveys reached the expected quality, both in RTK and DGNSS positioning.
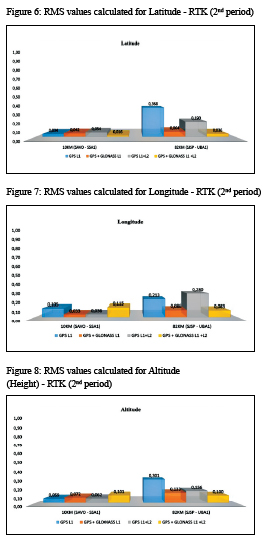
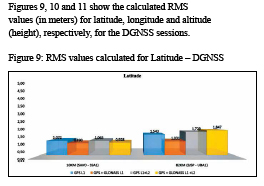
The RTK results indicated coordinates RMS values with centimeter level in the case of the 10-km baseline (SAVOSSA1), whereas RMS values with decimetric level were obtained for the 82-km baseline (SJSP-UBA1), with any processing option. It was observed that the use of L1 + L2 data improved the result of the SJSP-UBA1 baseline, as expected, being indifferent in the case of the shorter baseline, due to the more significant reduction of ionospheric refraction errors when differentiating observations in the latter case.
The use of combined GPS + GLONASS data decreased the RMS values of RTK coordinates when compared to those obtained with the use of GPS data only, probably due to the improvement of satellite geometry and the increase in the degrees of freedom in the processing. In addition, in most cases, the best RTK solutions corresponded to the GPS + GLONASS L1 + L2 option, as expected. Some GPS + GLONASS L1 results presented better RMS values than those obtained with GPS L1 + L2 in the 82-km baseline, indicating that possibly the use of more L1 observations was more beneficial than the use of dual frequency in this work, where the observations were carried out in 2017, thus in a period of solar activity close to the minimum (Figure 12).
In terms of coordinates (ambiguities) convergence time in RTK solutions, its reduction is clearly observed when using more than one GNSS system, due to the increased number of satellites (observations), and also when using two frequencies, as the first order effects of the ionosphere are eliminated in these cases.
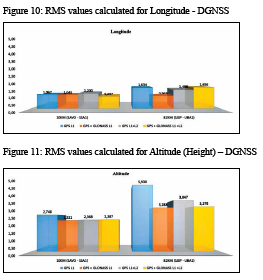
The DGNSS results reached metric quality in any processing option, since this determination is contaminated by noise and multipath errors in the pseudorange observations. Nevertheless, the RMS values obtained corresponded to only about 30% of the nominal navigation accuracy with GPS (9 m, horizontal, and 15 m, vertical, 95% of the time – US DoD, 2008), indicating a gain of quality when using this technique compared to single point positioning.
Under the specific conditions of this work, the attempt to fix ambiguities at the longest baseline using only GPS L1 observations led to the determination of incorrect integers, which indicates that, under these circumstances, the option for the FLOAT solution throughout the observation session would be more reliable.
References
BUNDESAMT FÜR KARTOGRAPHIE UND GEODÄSIE (BKG). Ntrip – Networked Transport of RTCM via Internet Protocol. Available in <https://igs.bkg.bund.de/ntrip/about>. Accessed on August 20, 2017(a).
BUNDESAMT FÜR KARTOGRAPHIE UND GEODÄSIE (BKG). BKG Ntrip Client (BNC). Available in <https://igs.bkg.bund.de/ntrip/bnc>. Acessed on August 20, 2017(b).
FERREIRA, S. C. N. E FORTES, L. P. S. Análise preliminar dos impactos do uso de mais de um sistema GNSS no posicionamento preciso. Revista Cartográfica do IPGH, Number 92, January-June 2016, pp. 31-51.
FORTES, L. P. S. Notas de aula, Posicionamento Geodésico por satélites artificiais. Rio de Janeiro, 2016.
INSTITUTO BRASILEIRO DE GEOGRAFIA E ESTATÍSTICA (IBGE). RBMC-IP – Rede Brasileira de Monitoramento Contínuo dos Sistemas GNSS em tempo real. Avaliable in https://ww2.ibge.gov. br/home/geociencias/geodesia/rbmc/ ntrip/. Acessed on March 28, 2018.
MACHADO, T. M. Avaliação de desempenho de receptores de GPS em modo estático e cinemático, 38p Thesis (Master in Agronomy) – Escola Superior de Agricultura Luiz de Queiroz, Piracicaba, 2008.
MONICO, J F.M.; PÓZ, A.P.D.; GALO, M.; SANTOS, M.C.; OLIVEIRA, L.C. Acurácia e Precisão: Revendo os conceitos de forma acurada. Bol. Ciênc. Geod., sec. Comunicações, Curitiba, vol. 15, number 3, p.469-483, jul-sept, 2009.
MONICO, J. F. G. Posicionamento pelo GNSS: Descrição, fundamentos e aplicações. 2. ed. São Paulo: Editora Unesp, 2008.
SEEBER, G. Satellite Geodesy: foundations, methods, and applications. Berlin/New York: Walter de Gruyter, 336p, 2003.
TAKASU, T. RTKLIB ver. 2.4.2 Manual, April 29, 2013. Avaliable in http://www.rtklib. com/prog/manual_2.4.2.pdf.
US DoD. GPS Standard Positioning Service (SPS) Performance Standard. 4th Edition, U.S. Department of Defense, September 2008. Avaliable in http://www.gps.gov/technical/ps/2008- SPS-performance-standard.pdf.











 (No Ratings Yet)
(No Ratings Yet)






Leave your response!