| Navigation | |
An Alternative Low Cost MEMS IMU/GPS Integration Scheme
|
||||||||||||||||||||
|
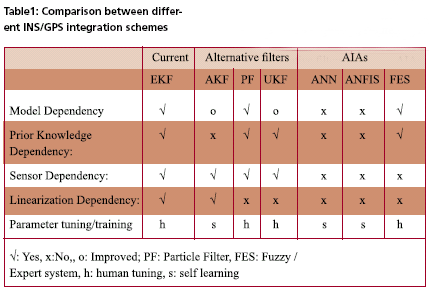
This article investigates the use of artificial neural networks for developing an alternative integration scheme of low cost Microelectromechanical System (MEMS) Inertial Navigation System (INS) and Global Positioning System (GPS) for vehicular navigation applications. The primary objective is to overcome the limitations of current INS/GPS integration scheme and improve the positioning accuracy during GPS signal blockages. The results presented in this article indicated that the proposed technique was able to provide 47% and 78% improvement in terms of positioning accuracy during GPS signal blockages. IntroductionWith the evolution of modern computer technology in hardware and software, the fi eld of artificial intelligence has been receiving more attention in the development of new generation technology. Artificial intelligence (AI), also known as machine intelligence, is defi ned as the intelligence exhibited by anything manufactured (i.e. artificial) by humans or other sentient beings or systems (should such things ever exist on Earth or elsewhere) [Cawsey, 1999]. It is usually hypothetically applied to general-purpose computers. The term is also used to refer to the field of scientific investigation into the plausibility of and approaches to creating such systems. Artificial intelligence has been verified as a successful and effective tool for providing solutions to certain engineering and science problems that can not be solved properly using conventional techniques [Cawsey, 1998]. The goal of applying artificial intelligent technologies is to provide intelligence and robustness in the complex and uncertain systems similar to those seen in natural biological species [Honavar and Uhr, 1994]. According to Russell and Norvig [2002], the techniques and the related research fi elds of artificial intelligence (AI) are given in Figure (1). It is well known that Kalman filter approach has been widely applied as the core algorithm for INS/ GPS scheme for many navigation applications. Although it represents one of the best solutions for INS/ GPS integration applications, it has limitations in terms of model dependency, prior knowledge dependency, sensor dependency, and linearization dependency for general INS/GPS integrated navigation applications [Chiang, 2004]. Consequently, in order to overcome or reduce the impact of these limitations, several research works have been conducted to investigate possible alternative algorithms for INS/GPS integration scheme [see for example, Chiang, 2004]. The incorporation of Artificial Intelligence Algorithms (AIAs) for developing alternative INS/GPS integration scheme is fueled by the need for intelligent systems and the limitations with the current INS/GPS integration scheme. Among artifi cial intelligent methodologies shown in the Figure (1), ANNs have been extensively studied with the aim of achieving human-like performance, especially in the field of pattern recognition and robot control and navigation [Mandic and Chambers, 2001]. ANNs are composed of a number of nonlinear computation elements which operate in parallel and are arranged in a manner reminiscent of biological neural interconnections. In addition, ANNs are designed to mimic the human brain and duplicate its intelligence by utilizing adaptive models that can learn from the existing data and then generalize what it has learnt [Ham and Kostanic, 2001]. Therefore, this article attempts to evaluate an alternative INS/GPS integration schemes developed by the authors for general land vehicular navigation and positioning applications using low cost MEMS INS. Problem statementAccording to Chiang [2004], the limiting factors of Kalman filter based INS/GPS integration are given in brief as follow; Model dependencyGenerally speaking, the development a model to be used in the Kalman fi lter starts with the construction of a full scaled “true-error model”, whose order is then reduced based on the prior knowledge and the insight gained into the physics of the problem, covariance analysis, and simulation [Salychev et al, 2000]. Typically, the dynamics model is based on an error model for three position errors, three velocity errors, and three attitude errors in an INS (the system error states). These errors are also augmented by some sensor error states such as accelerometer biases and gyroscope drifts, which are modeled as stochastic processes (i.e., 1st Gauss Markov process or random walk) [Rogers,2003]. In fact, there are several random errors associated with each inertial sensor. Therefore, it is usually diffi cult to set a certain stochastic model for each inertial sensor that works efficiently at all environments and reflects the long term behavior of the sensor errors. Hence a model-less navigation algorithm that can perform the self-following of the vehicle under all-conditions is required. Prior knowledge dependencyAs mentioned previously, some initial knowledge is required to start a Kalman fi lter, such as the state transition matrix (Fk,k-1), the measurements design matrix (Hk), the noise coefficient matrix (Gk-1 ), the system noise covariance matrix (Q) and the measurements noise covariance matrix (R). Among them, the Q and R matrices are the most important factors for the quality of the Kalman filter estimation for an INS/ GPS integrated system. Theoretically, the optimal Q and R matrices can guarantee the optimality of the estimation; however, tuning the Q and R matrices can be time consuming and it requires experience and background in both systems. Consequently, the requirement of human intervention for Q/R tuning is very high. In other words, the tuning process can be regarded as a special form of learning as it is usually done by an expert and needs time to obtain the optimal solution. Consequently, a new navigation algorithm that can reduce the level of human intervention and is capable of learning by itself to adapt the latest dynamic model is preferred. Sensor dependencyThe need to re-design algorithms based on the Kalman filter (i.e., states) to operate adequately and efficiently on every new platform (application) or different systems (e.g. switch from navigation grade IMU to tactical grade IMUs) can be very costly. In addition, the Q and R matrices tuning is heavily system dependent [Vanicek and Omerbasic, 1999]. As a result, a new navigation algorithm that is adaptable and can reduce the level of sensor dependency is highly desirable. Linearization dependencyINS/GPS integration for land vehicular navigation is composed of non-linear dynamic in nature. However, since the principle of Kalman fi ltering is to estimate a linear dynamical model using a recursive algorithm along with certain stochastic information, the linearization of INS or GPS dynamics model is required [Brown and Huang, 1992]. However, the linearization process is usually a 1st order approximation process that results in deviations between the assumed “true error model” and the real “true error model”. As a result, a new navigation algorithm that is nonlinear in nature and can reduce the impact of linearization is preferred. ObjectivesThe objectives of this article are to: (1) provide a brief review about the latest development of alternative INS/GPS integration scheme and (2) evaluate an alternative INS/GPS integration scheme developed by the authors for the use of a low cost MEMS INS/GPS integrated system. Recent development of alternative INS/GPS Integration chemesThe primary objective of developing alternative INS/GPS integration scheme is to reduce the impact of remaining limiting factors and improve the positioning accuracy during GPS signal outages. The recent research activities involved with developing alternative schemes for general navigation applications fall into two categories: Alternative fi ltersXu [1996] suggested a new selflearning navigation fi lter associated with probability space and non- Newtonian dynamics. This new filter relied basically on the information contained in measurements on the vehicle: position fixes, velocities and their error statistics. Mohamed [1999] suggested Adaptive Kalman filter (AKF) based INS/GPS integration architecture. Fredrik et al., [2002] proposed a framework for positioning, navigation and tracking problems using particle fi lters (sequential Monte Carlo methods). It consisted of a class of motion models and a general non-linear measurement equation in position. Frykman [2003] suggested particle filters based aircraft integrated navigation with the utilization of INS and GPS. Shin and El-Sheimy [2004] suggested an UKF based INS/GPS integration scheme. AIAsMeng and Kak [1993] suggested a neural network-based navigation algorithm for a mobile robot. Townsend et al., [1994] proposed a Radial Basis Function (RBF) Networks approach for mobile robot positioning. Dumville and Tsakiri [1994] utilized a neural network to integrate DR and GPS for land vehicle navigation. Chansarkar [1999] utilized RBF networks for GPS positioning and navigation. Forrest et al., [2000] suggested an inertial navigation data fusion system employing an unsupervised neural network as the data integrator to estimate INS errors. Ojeda and Borenstein [2002] proposed a fuzzy logic rule-based position estimation algorithm for mobile robots as one of the prototypes of marsian rovers. As for INS/GPS integration, Chiang and El-Sheimy[2002] and Chiang et al., [2003] first suggested an INS/ GPS integration architecture utilizing Multi-Layer Feed-Forward Neural Networks (MFNNs) for fusing data from DGPS and either navigation grade IMUs or tactical grade IMUs. Chiang [2003] proposed an MFNN based INS/GPS architecture for integrating IMUs with Single Point Positioning (SPP). Chiang [2004] proposed an optimal GPS/ MEMS integration architecture for land vehicle navigation utilizing neural network. Chiang and El- Sheimy [2004] proposed the idea The common characteristic of those research works is to reduce the impact of those limiting factors mentioned above. According to the results and conclusions given by Mohamed [1999], Frykman [2003], Ojeda and Borenstein [2002], Shin and El-Sheimy [2004], Chiang [2004] and El-Sheimy and Abdel- Hamid [2004], a comparison between different INS/GPS integration schemes is given in Table 1. As indicated in Table 1, the AIAs are able to provide more advantages for implementing alternative INS/ GPS integration schemes. Due to the limited scope of this article, only ANN based INS/GPS integration scheme developed by the authors will be discussed as an example to demonstrate the benefits of incorporating of incorporating AIAs as the core component for alternative INS/GPS integration schemes. ReferencesBrown, R. G. and Hwang, P. Y. C. (1992): Introduction to random signals and applied Kalman filtering. John Wiley & Sons, Inc. New York. Cawsey, A. (1998): The Essence of Artifi cial Intelligence, Prentice Hall PTR. Chansarkar, M. (1999): GPS Navigation using Neural Networks, Proceeding of ION GPS-99, Nashville, TN. Chiang, K.W. and El-Sheimy, N. (2002): INS/GPS Integration using Neural Networks for Land Vehicle Navigation Applications, Proceedings of the US Institute of Navigation (ION) GPS’2002 meeting, September 24-27, 2002 – Oregon Convention Center, Portland, Oregon, USA (CD). Chiang, K.W., Noureldin, A., and El-Sheimy, N.(2003): Multi-sensors Integration using Neuron Computing for Land Vehicle Navigation, GPS Solutions.,Vol. 6, No. 3, pp. 209-218. Chiang, K.W.(2003): The Utilization of Single Point Positioning and a Multi-Layers Feed-forward Network for INS/GPS Integration, Institute of Navigation (ION) GPS’2003 meeting, September 9-12, 2003 – Oregon Convention Center, Portland, Oregon, USA (Best Student Paper Award)(CD). Chiang, K.W.(2004): Development of an Optimal GPS/MEMS Integration Architecture for Land Vehicle Navigation Utilizing Neural Network. Journal of Global Position System and CPGPS student paper competition (Best Student Paper Award). Chiang, K.W. and El-Sheimy, N. (2004): Artificial Neural Networks in Direct Georeferencing, Photogrammetric Engineering and Remote Sensing, July, 2004 (Invited column paper). Dumville, M. and Tsakiri, M. (1994): An Adaptive Filter for Land Navigation using Neural Computing., In: Proc. of the 7th International Technical Meeting of the Satellite Division of the Institute of Navigation, ION GPS-94, Salt Lake City, USA. Forrest, M., Spracklen, T., and Ryan, N. (2000): An inertial Navigation data fusion system employing an artificial neural network as the data integrator. In: Proc. of the ION NTM 2000 Anaheim, CA. January 26-28, 2000 (CD). Frykman, P. (2003): Applied Particle Filters in Integrated Aircraft Navigation System, (M.sc, Thesis), Department of Electrical Engineering, The university of LinkÄoping, Sweden. Fredrik, G., Niclas B., Urban, F., Jonas, J., Rickard, K., and Per- Johan, N. (2002): Particle filters for positioning, navigation and tracking. IEEE Transactions on Signal Processing, Vol. 50, No. 2, 2002. Ham, F.M. and Kostanic, I. (2001): Principles of Neurocomputing for Science and Engineering. McGraw-Hill. Honavar, V. and Uhr L. (1994): Artificial Intelligence and Neural Networks: Steps Toward Principled Integration, Boston: Academic Press. Mandic, D.P. and Chambers, J.A. (2001): Recurrent Neural Networks for Prediction: Architectures, Learning Algorithms and Stability. John Wiley & Sons Meng, M. and Kak, A.C.(1993): Mobile robot navigation using neural networks and nonmetrical environment models, IEEE Control Systems, pp. 30-39, October 1993. Mohamed, A. H. (1999): Optimizing the Estimation Procedure in INS/ GPS Integration for Kinematic Application. UCGE Reports Number 20127, Department of Geomatics Engineering, The University of Calgary. El-Sheimy, N. and Abdel-Hamid, W. (2004): An Adaptive Neuro- Fuzzy Model to Bridge GPS Outages in MEMS-INS/GPS Land Vehicle Navigation. GNSS 2004, ION, September 21-24, 2004 – Long Beach, California, USA. Ojeda, L. and Borenstein, J. ( 2002): FLEXnav: Fuzzy Logic Expert Rule-based Position Estimation for Mobile Robots on Rugged Terrain., Proceedings of the 2002 IEEE International Conference on Robotics and Automation, Washington DC, USA, 11 – 15 May 2002, pp. 317-322. Rogers, R.M. (2003): Applied Mathematics in Integrated Navigation Systems, Second Edition. American Institute of Aeronautics and Astonautics, Inc. Russell, S.J. and Norvig, J (2000): Artifi cial Intelligence: A Modern Approach ,Prentice Hall; 2nd edition , December 20, 2002 Salychev, O.S., Voronov, V.V., Cannon, M.E., Nayak, N., and Lachapelle, G. (2000): Low Cost INS/GPS Integration: Concepts and testing. In Proceedings of the ION National Technical Meeting, pages 98–105, Anaheim, CA Shin, E. H. and El-Sheimy, N. (2004): An Unscented Kalman Filter for In-Motion Alignment of Low Cost IMUs. Proceeding of IEEE PLANS 2004, Monterey, California, USA. Townsend, N.W., Brownlow, M., and Tarassenko L.(1994): Radial Basis Function Networks for Mobile Robot Localisation, Proceedings of the 1994 INNS World Conference On Neural Networks, Vol.2, pp. 9-14. Vanícek, P. and Omerbasic M. (1999): Does a navigational algorithm have to use Kalman fi lter? Canadian Aeronautical and Space Institute Xu, B. (1996): A New Navigation Filter. PhD Thesis, Technical Report No. 182, The Department of Geodesy and Geomatics Engineering, University of New Brunswick, Fredericton, NB Canada. |
||||||||||||||||||||
|
||||||||||||||||||||
|













 (No Ratings Yet)
(No Ratings Yet)





