| Geodesy | |
Datum transformations using exclusively geodetic curvilinear coordinates without height information
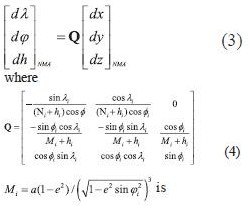
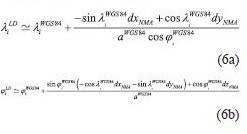
WGS84 is a widely used reference system for navigation purposes, especially using GNSS technologies (Hoffman-Wellenchoff et al. 1997). Furthermore, navigation tools like Google Earth, uses WGS84 coordinates for point acquisition. A main problem is the fact that the major part of national mapping infrastructure (for each country), usually referred to a local (old type) geodetic datum. National Mapping Agencies (NMA’s) in many cases provide 3 translation parameters in order to transform in approximation (e.g with 5-10 meters accuracy) the WGS84 geocentric coordinates to a local datum, using the following formula (pointwise): radius of prime vertical, a, e2 are the major semi-axis and the squared eccentricity of a particular spheroid respectively The methodNevertheless, when the geodetic coordinates are introduced, the height information could be either neglected (e.g for vehicle navigation), or even the introduced height information is derived from different source. E.g Google Earth height information uses global DEM models, which are not consistent with the geodetic heights. An efficient way to overcome this problem is to express the Cartesian system translations to curvilinear coordinate differences respectively. This could be done using the relation between them, given by (e.g Okkeke 1998, Ampatzidis 2006, Kotsakis 2007): point’s radius of the meridian Hence, we can express now the curvilinear differences between the WGS84 and the local datum, as follows(angular units must be in radians): Taking account (5), the transformation between WGS84 and GGRS87 is: It can be implied that in the curvilinear coordinate transformation is a function of Cartesian system translations, initial reference frame latitude, longitude and spheroid’s associated quantities (major semi-axis and eccentricity). The whole procedure is more complicated than the case of Cartesian coordinates, reflecting the fact that the transformation referred now to a non-Euclidean surface (spheroid). The transformation of local datum to WGS84 curvilinear coordinatesIn the case of the need of transformation from the local datum to WGS84 curvilinear coordinates, the method could also stand for this purpose. The only modification is the introduction of the translation parameters with different sign. Eq. (6) takes now the following form: Eq. (9) gives the advantage of the direct transformation between the local datum and the WGS84 without introducing any geodetic height information, which is quite problematic in old type of datums. The major semi axis refers to the local datum spheroid. Hence, from any map (old or new) the transformation could be implemented with a straightforward procedure. ConclusionsIn the present paper is presented a method of transforming curvilinear coordinates from WGS84 to local datum and vice versa. The basic idea of the method lies on the connection between the translations of a Cartesian system and curvilinear differences on a particular spheroid. The strategy could be useful in the cases of either neglecting or having inconsistencies on height information for one (or both) geodetic system(s). ReferencesAmpatzidis, D. (2006), Study and data processing for the implementation of differential 3-D transformation on the Greek area. Diploma Thesis submitted to the Department of Geodesy and Surveying, Aristotle University of Thessaloniki (in Greek). Okkeke, F. I. (1998), The curvilinear datum transformation model. Deutsche Geodatische Kommission, Reihe C, Heft Nr. 481, Munchen. Hellenic Cadastral and Cartographic Organization-HCCO (1987), The Greek Geodetic Reference System 1987. Report published from the HCCO. Hoffman-Wellenhof B., H. Lichtenegger and J. Collins (1997), Global Positioning System. Theory and Practice. Fourth revised edition. Springer. Kotsakis C. (2007), Transforming ellipsoidal heights and geoid undulations between different geodetic reference frames, Journal of Geodesy, vol. 82, pp. 249-260. Vanicek, P. and E.J. Krakiwsky (1982), Geodesy: The Concepts, North-Holland Publishing Company, New York
|





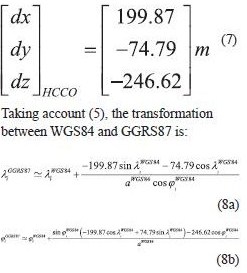
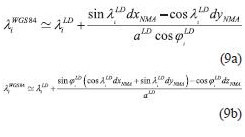











 (18 votes, average: 4.11 out of 5)
(18 votes, average: 4.11 out of 5)




Leave your response!