Comparing Global Geoids

EL Hassan EL BRIRCHI Mathematics Computing and Geomatics Department Ecole Hassania des Travaux Publics, Casablanca, Morocco

Pr Driss EL AZZAB Geo resources and Environment Laboratory, Technical Science Faculty, Sidi Mohamed Ben Abdellah University, Morocco

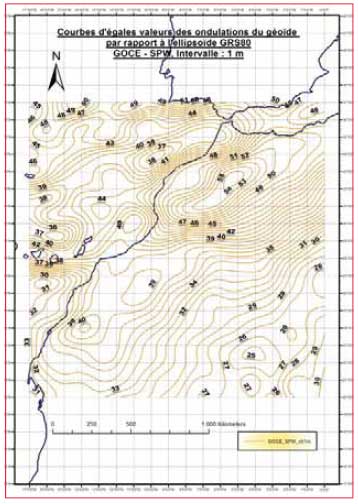
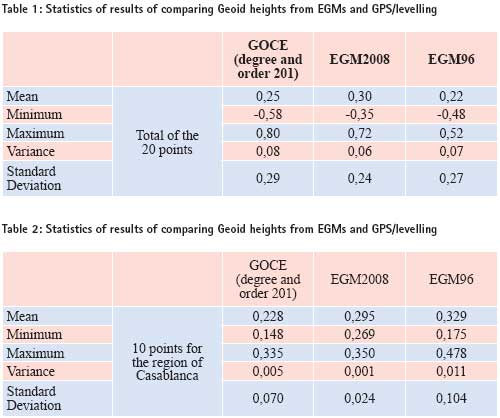
Rather than classical instruments and methods for collecting spatial data, GNSS facilitate and enhance collecting time and range.
GNSS 2D positioning accuracy is well defined. According to the receiver model, the software, the positioning Mode, the available corrections used, the 2D positioning accuracy vary from few meters to mm. However the altimetry positioning with GNSS is less accurate than 2D one.
Without an accurate Geoid reference earth surface, the levelling survey by GNSS couldn’t be done with sufficient accuracy needed for several fields of survey like construction or water management projects.
As a step in the way of computing a precise geoid surface over Morocco, the aim of this paper is to compare global geoid models especially regarding the improvement shown in the spatial determination of the gravity field during the last few years.

Geoid Determination

Methods for computing geoid models

Geoid as physical earth reference surface is defined as an equipotential surface of the gravity field of the earth g. It is also approximated by the mean sea level to get a point with altitude 0 in order to fix altimetry datum and enable classical levelling.

The determination of geoid is meant as the compute of geoid heights from the reference ellipsoid. This is done by several methods:

– Computing geoid heights using global models of spherical harmonics coefficients. This method allows the determination of long or medium wavelength part of geoid according to the maximum degree and order of the model.

– In order to take into account the short wavelength part of the geoid we use gravimetric models which are based on transformation of residual gravity anomaly into geoid heights by the Stokes integral. The terrain effect is also computed especially in regions with rough topography

– Comparing ellipsoidal height measured by GNSS and physical height measured by classical levelling allow the determination of geoid height.

More details on these methods could be found in (Hofmann- Wellenhof and Moritz 2005)

Geoid determination over Morocco

Two gravimetric geoids are computed over the north of Morocco. The first one is MGG97 (Benaim et al 1997). It is based on OSU91A (Rapp et al 1991) as global geopotential model and a set of land measured free air anomaly points.
The second one is MORGEO05 (Corchette et al 2007). Improvement is due to the use of EIGEN CG01C (Reigber et al 2006) as global geopotential model for the estimation of long and medium wavelength. SRTM 90M as global digital terrain model is also used to take into account terrain correction in the determination of MORGEO05.

Global geopoteantial model

Spatial gravity missions

During the last decade three spatial gravity missions are launched in order to improve the knowledge of the gravity field. These three missions are:

– CHAllenging Minisatellite Payload (CHAMP) (Reigber et al. 1996)

– Gravity Recovery And Climate Experiment (GRACE) (GRACE 1998)

– Gravity field and steady-state Ocean Circulation Explorer (GOCE) (ESA 1999)

The last one is launched by Europeen Spatial Agency (ESA) in March 2009 and proposes the determination of geoid until the wavelength of 200 km (resolution of 100 km). An improvement of accuracy is also proposed by GOCE: 1 cm for geoid height accuracy and 1 mgal for gravity anomaly accuracy.

Earth Geopotential Model

Several Earth Geopotential Models have been computed according to the spherical harmonic development of the gravity potential. Due to the limitation of the spatial methods some EGM included information from land measured gravity data in addition to the spatial data. A list of these models could be found in the International Centre for Global Earth Models (ICGEM).

Figure 1: Contour Map for geoid height above GRS80 computed from GOCE Geopotential Model (Interval 1 m) (Source: EL BRIRCHI & EL AZZAB 2011)

Used Data

In this work we compare some EGMs to Geoid heights computed from GPS/levelling data. We use 20 GPS/ Levelling points over the study area. The EGMs evaluated are:
– GOCE geopotential models provided by the European Space Agency.
– EGM96 (Lemoine et al 1998) developed until 360 maximum of degree and order
– EGM2008 (Pavlis et al 2008) developed until 2160 maximum of degree and order

Results

Figure 1 shows the contour map of geoid height computed above GRS 80 ellipsoid using GOCE geopotential model. This result represent wavelength of geoid until 100 km resolution.

After computing differences between geoid heights from GOCE, EGM2008 and EGM96 and from GPS/levelling determinations for the 20 control points we summarize statistics of the results in table 1.

We also limit the test for the region of Casablanca using only 10 GPS/ levelling points. Results are in table 2.

We note that EGM96 used in this paper is corrected by a term of – 0.53 m to fit better WGS84 ellipsoid. From table 1 and table 2 we could conclude that EGM2008 is better than GOCE and the corrected EGM 96 on the criterion of small standard deviation. The choice of better global geoid for all the area of Morocco couldn’t be done unless we use GPS/ levelling points over all the study area.

Results obtained for the region of Casablanca show that EGM2008 could be used for levelling by GPS. It is also possible because of smooth topography in this region.

Conclusion

New EGMs enhance considerably the determination of long and medium wavelength over Morocco. More tests are necessary to confirm the choice of EGM2008 especially in mountainous regions in Morocco where terrain effects should be taken into account.

References

Benaim E.H., Swassi A.M. & Sevilla M.J. (1997). The First Northern Moroccan Gravimetric Geoid. Journal of Physics and Chemestry Of the Earth, Vol. 23, No 1, pp 65-70. Ed Pergamon.

Corchete V., Chourak M., Khattach D. & Benaim E.H. (2007). The highresolution gravimetric geoid of Morocco: MORGEO. Journal of African Earth Sciences, 48, pp 267-272.

EL Brirchi E.H. & EL Azzab D. (2011). Calcul d’un nouveau Géoïde au Maroc à partir des données de la mission de gravimétrie spatiale GOCE et utilisation des SIG pour sa validation par GPS et Nivellement. Geo Observateur Journal N° 19, CRTS, Rabat (IN PRESS)

ESA. (1999). Gravity field and steadystate ocean circulation mission. Rapport Spécial, ESA publication division, ESA SP-1233 (1), c/o ESTEC, Noordwijk, Netherland.

GRACE. (1998). Gravity Recovery and Climate Experiment : Science & Mission Requirements Document, Revision A, JPLD-15928, NASA’s Earth System Science Pathfinder Program.

Hofmann-Wellenhof B. et Moritz H. (2005). Physical Geodesy. SpringerWienNewYork, Autriche.

Lemoine, F.G., Kenyon, S.C., Factor, J.K., Trimmer, R.G., Pavlis, N.K., Chinn, D.S., Cox, C.M., Klosko, S.M., Luthcke, S.B., Torrence, M.H., Wang, Y.M., Williamson, R.G., Pavlis, E.C., Rapp, R.H., Olson, T.R. (1998). The Development of the Joint NASA GSFC and the National IMagery and Mapping Agency (NIMA) Geopotential Model EGM96; NASA Technical Paper NASA/TP1998206861, Goddard Space Flight Center, Greenbelt, USA.

Pavlis, N.K., Holmes S.A., Kenyon S.C., Factor J.K. (2008). An Earth Gravitational Model to Degree 2160: EGM2008; presented at the 2008 General Assembly of the European Geosciences Union, Vienna, Austria, April 13-18.

Rapp, R.H., Wang, Y.M., Pavlis, N.K. (1991). The Ohio State 1991 Geopotential and Sea Surface Topography Harmonic Coefficient Models; The Ohio State University, Department of Geodetic Science, Report No. 410, Columbus/Ohio.

Reigber C., Bock R., Förste Ch., Grunwaldt L., Jakowski N., Lühr H., Schwintzer P. et Tilgner C. (1996). CHAMP Phase B-Executive Summary. G.F.Z., STR96/13.

Reigber, C., Schwintzer, P., Stubenvoll,R., Schmidt,R., Flechtner, F., Meyer, U., König, R., Neumayer, H., Förste, C., Barthelmes, F., Zhu, S.Y., Balmino, G., Biancale, R., Lemoine, J.-M., Meixner, H., Raimondo, J.C. (2006). A High Resolution Global Gravity Field Model Combining CHAMP and GRACE Satellite Mission and Surface Data: EIGEN-CG01C; Scientific Technical Report STR06/07, GeoForschungsZentrum Potsdam