| Geodesy | |
Determination of geoid in Saudi Arabia using global gravity model and GPS/benchmark data
The results may indicate that refinement of undulation of Global Gravity Field Model with GPS/Benchmark data have given the preliminary values of geoid undulations acceptable for practice purposes for the Kingdom |
 |
|
 |
|
Existing national geodetic vertical network of Saudi Arabia
The current National Geodetic Vertical Network (NGVN) in the Saudi Arabia is based mainly upon a series of leveling runs carried out during 1966 – 1970. About 54 levelling circuits were carried out over a distance of 1,952 km of first order leveling and 13,002 km of second order levelling and around 2,500 benchmark established at an average of 6 km. These benchmarks are generally along the major routes and 50-100 m off the road.
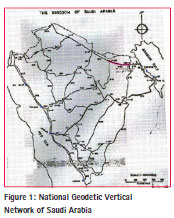
The accuracy was specified as first, second and third order leveling criteria of classification of leveling network. Around 809 benchmarks of the 2,500 ground markers were spirit levelled. The rest were heighted by reciprocal vertical angles. The vertical datum based on six recording tidal observatories have data from April 1969 to March 1970. These observatories are located in Jeddah, Yanbu, Al-Wajh, Gizan, Manifah and Ras Tanurah, as shown with a blue colored square in Figure 1. (Nakiboglu, S.M.et all, (1994).
Concrete monuments were installed in all non-rocky and non-sandy locations. In rocky locations where excavation proved difficult, a shortened central tube was used. In sandy locations liable to erosion, the three m pipe marker was installed with witness posts.
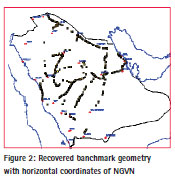
A comprehensive field reconnaissance has been carried out based on the existing benchmarks. Height data was collected, classified and evaluated for GPS surveys. Many of the benchmarks of NGVN have subsequently been destroyed and/or lost during development work, and that only as few as 20% has been recovered in some areas (see Figure 2).
Additional benchmarks established through out the projects by municipalities and other agencies have been included in the process. (See Figure 3)
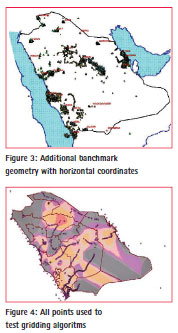
By examining the existing benchmarks, it was decided that spirit leveling would be carried out in mostly those areas where existing benchmarks were inadequate and the geoid, steep. In this context, we selected South-West and South of Saudi Arabia for spirit leveling. The total distance of monumented lines of spirit leveling works was around 2,000 km, where benchmarks were constructed at 5 km intervals and named in a way to be consistent with the existing leveling network. As a result, the total number of benchmarks used to refine The Earth Geo-potential Model EGM96 is about 3,800 points. (see Figure 4)
Vertical control analysis showed that the existing leveling network was adjusted to a mean sea level value derived from the tidal observation at Jeddah, Yanbu, Al Wajh, Jizan, Manifah and Ras Tanurah. But, unfortunately, the uncertainties of benchmarks elevations are not available. The only estimation regarding the reliability of benchmarks may be deduced from the difference in elevation obtained from opposite runs that shall not be greater than first and second order leveling criteria of classification of leveling network. Therefore, this concept has been followed during the work.
Relations between orthometric heights and geoid
The GPS measured heights are measured from the ellipsoid; therefore, they need to be converted into an orthometric height system. The current methods of converting GPS elevations to orthometric elevations (Martin, Daniel J. ( 2001)) are:
– To incorporate a priori geoid undulation data in three-dimensional (3D) adjustment, which holding the benchmark elevations fixed for stations with known values, have to be determined by spirit leveling. The minimum number of benchmarks should be four and well distributed throughout the region.
– Determination of orthometric heights from GPS vector baseline data involves performing 3D adjustment without using geoid undulation data. In this method, the benchmarks elevations are held fixed while using zero values for geoid undulations in a 3D adjustment. This interpolates the geoid undulation values for the remaining stations in the region. Here also, a minimum of four known benchmarks are needed and preferably more than four well distributed benchmarks to achieve valid results.
– The best method is to compute the actual geoid undulation difference details from gravitational anomalies for the desired stations, wherever centimeter accuracies are derived.
The ultimate aim for the vertical network is to determine a geoid surface across the region, in such a way that GPS observations can be corrected so that they agree with the orthometric height datum.
An initial assessment of problems associated with the geoid was made using the observed WGS-84 coordinates with GPS points across the region. From the differences between GPS and orthometric height, the initial values for the geoid separation, NMSL (see Figure 5) was determined.

This figure was then compared with the value given by the NEGM96 global Earth model. The statistical results are shown in Table 1.
RMS of residuals variations is 0.749 m. However, considering the known accuracy of EGM96, the type of terrain and the area covered, these variations are far greater than would be expected.
Global gravity field model, EGM96
The global Earth Gravity Model for 1996 (EGM96) is the result of a collaboration between the National Imagery and Mapping Agency, NASA Goddard Space Flight Centre, and the Ohio State University. The collaboration was for covering the Earth gravity field up to degree and order 360. This corresponds to a spatial resolution of up to 55 km and models the geoid within an accuracy of about 40 cm (global average).
For a further refinement of the EGM96 in the Saudi Arabia, surface point information has to be introduced. A point separation of less than 30 km is needed to cover the short wave length part of the harmonic development of the Earth gravity field (degree 361 . . . 10000, 0.5 m . . . 0.01 m geoid undulation, point separation 30 km . . . 1 km (grid wise)).
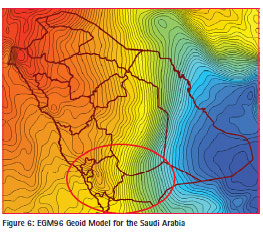
Figure 6 shows the part of the EGM96 model that covers the Saudi Arabia. Proceeding along the 19-degree latitude, circle from west to east (from Baha to Sharurah, marked with the circle in red), a steep increase of the geoidal height of about 5 m (from 3 m to -2 m) occurs over a short distance of less than 100 km.
Determination of geoid throughout the Kingdom
In order to determine the geoid throughout the Kingdom, recovered benchmarks (BM) from existing vertical network, selected constraining points on water surfaces around The Kingdom and newly-established benchmarks (GPS-BM) where the geoid steep and benchmark established through projects by different agencies, have been used. The orthometric heights of all the points on ground are known from leveling activities. With ellipsoidal heights coming from global navigation satellite system (GNSS), we have the geoid heights for all these points from the famous relation (1).
Furthermore, the points on water surfaces have known orthometric heights of zero. Since these points are used exclusively for constraining purposes, it is thought to be sufficient to take their geoid heights from EGM96. This gives us enough data to estimate the ellipsoidal height at these points, if needed.
Both sides of Equation (1) may be arrived at by separate means. EGM96 model can give one estimate of geoid height (NEGM96) and removing the orthometric height from an ellipsoidal height (NMSL, geoid as derived from actual survey data) will yield another. The residual difference between these two estimates and NMSL was processed to develop a model of the correlated signal according to:
![]()
where:
H: is the orthometric
height; h: is the ellipsoidal height;
N: is the geoid height.
This process involved determining a conversion surface that approximated the correlated signal existing in GNSSBM residuals ( NEGM-MSL) and NMSL. In this context we tested the following algorithms with the powerful software packages ’Golden Surfer 8’ and homemade software for the determination of the analytical geoid and residual geoid surface (Golden Software, Inc, Briggs, I. C. (1974), Nakagawa, H. et al (2003), Ghilani, Charles D. et all. (2002), Journel, A. G. et all. (1978), Kitanidis, P. K. (1997), Martensson, S. (2002)).
– Bi-Cubic Spline;
– Inverse Distance to a Power;
– Kriging; – Least Squares Collocation;
– Modified Shepard’s;
– Moving Average;
– Polynomial Regression;
– Trigonometric Function; and
– Thin-Plate Smoothing Spline based on Collocation Matrix
Initial tests revealed better results of two algorithms when compared to others, for GNSS-BM residuals ( NEGMMSL) and NMSL. These were: Kriging and Thin-Plate. Thus, we continue herein with these algorithms only.
Each algorithm was used to fit a surface to the available points in hand. Then that surface was used to interpolate for the heights at the same points (base points) and at the points that are not used to fit a surface (rover points) we have on land. This interpolation was done using Biharmonic Spline algorithm (Sandwell, D. T. (1987).
Since we already know the heights of these points, and since we are using unified interpolation algorithm, we could then judge which of the two gridding techniques give better results for our specific test case.
All this was done twice – once with the geoid (NMSL) heights of the points themselves, and once with the differences between these heights and those acquired from the global Earth Gravity Model for the year 1996 (EGM96_N), as shown in Figure 6 for Saudi Arabia. The second methodology allows us to get rid of the trend and benefit of the precision of EGM96.
Thin Plate Surface Fitting using Least Squares Collocation Matrix Algorithm
This mathematical algorithm can be efficiently applied to geostatistical problems, where a thin-plate smoothing spline (f) is implemented such that it is the unique minimizer of the weighted sum:
P*E(f) +(1-P)*R(f) (3)
with E(f) the error measure
E(f) = sum_j { | Y(:,j) – f(X(:,j)) |^2 : j=1,…,n } (4)
and R(f) the roughness measure
R(f) = integral (D_1 D_1 f)^2 + 2(D_1 D_2 f)^2 + (D_2 D_2 f)^2 (5)
Here, the integral is taken over the entire 2-space, and (D_i) denotes differentiation with respect to the (i-th) argument. Hence, the integral involves the second derivatives of (f). The smoothing parameter (P) is chosen (ad hoc fashion) according to dependence on the sites X.
In other words, thin-plate spline approximations (f) can be created such that they satisfy, approximately or exactly, the equation for given data values (z) for z = f(x,y), at given scattered data sites (x, y) in the plane. The associated collocation matrix is provided implicitly. The spline created is in st form, as are its first-order derivatives.
Within the calculations, thin-plate smoothing spline builds and uses collocation matrix for scattered data, implicitly. This makes this algorithm powerful (Golden Software, Inc).
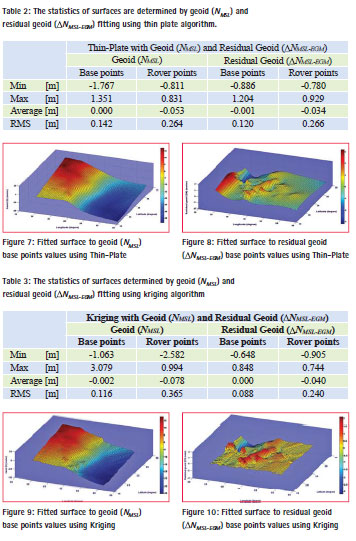
Thin Plate algorithm was used to fit a surface to the geoid (NMSL) and residual geoid ( NMSL-EGM) in hand separately. Then those surfaces were used to interpolate for the geoid heights (NINTP), residual geoid heights ( NINTP) at the same base points and at the rover points, we had on land.
The RMS of differences between geoid height and interpolated geoid height of base and rover points, residual geoid height and interpolated residual geoid height of base and rover points, has been found 0.142 m, 0.264 m, 0.120 m, and 0.266 m respectively; see Table 2. The fitted surfaces are shown in Figures 7 and 8.
This geometrical elevation grid is used in computing the residuals of the geoid heights computed from the EGM96, and adding appropriate corrections to the geoid heights of EGM96, according to the relationship shown in (2).
Surface Fitting based on Kriging Algorithm
This geostatistical algorithm has been used worldwide in various similar cases. Kriging is a technique that provides the Best Linear Unbiased Estimator of the unknown fields. It is a local estimator that can provide the interpolation and extrapolation of the originally sparsely sampled data that are assumed to be reasonably characterized by the Intrinsic Statistical Model (ISM). An ISM does not require the quantity of interest to be stationary, i.e., its mean and standard deviation are independent of position, but rather its covariance function depends on the separation of two data points only (Golden Software, Inc), Kitanidis, P. K. (1997), i.e.
E [(z(x) – m)(z(x’) – m)] = C(h) (6)
where m is the mean of z(x) and C(h) is the covariance function with lag h, with h being the distance between two samples x and x’:
![]()
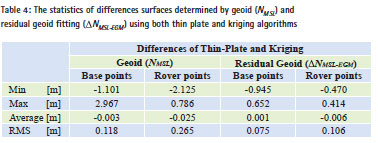
While the RMS of differences between geoid height and interpolated geoid height of base and rover points, residual geoid height and interpolated residual geoid height of base and rover points, has been found 0.116 m, 0.365 m, 0.088 m, and 0.240 m respectively see Table 3. The fitted surfaces are shown in Figures 9 and 10.
Results and discussions
All these analytical surfaces can be considered to compute the residual geoid heights with respect to the EGM96 surface throughout Saudi Arabia. Then, these corrections can be added to the corresponding EGM96 geoid heights to obtain improved geoid heights at these points.
In order to estimate the accuracy, comparisons have been made for both cases of geoid and residual geoid using two algorithms mentioned above. The statistical results are seen in Table 2, Table 3 and Table 4 for geoid and residual geoid fitting for both algorithms respectively. It is reasonable to interpret the results as geoid precision. These discrepancies are due to error sources from GPS and leveling surveys, mathematical model used as well as from the EGM96 itself.
The results in Table 3 indicate that Kriging has yielded the best fitting analytical surface for residual geoid fitting. Therefore, this algorithm was used for the computation of conversion surface of Saudi Arabia.
The geoid conversion surface is estimated to yield decimeter level precision geoid height throughout the Kingdom. Of course, the precision varies depending on the proximity to GPS leveled benchmarks. It is higher in the vicinity of such points and gets lower as the distance gets higher.
It is to be pointed out that the geoid conversion surface of Saudi Arabia input data is not error free. It can be concluded that both ellipsoidal heights determined by GPS techniques and orthometric heights determined by geometric leveling have precision in centimeter level.
The RMS of differences between residual geoid height and interpolated residual geoid height of base points and the RMS of differences of two algorithms have been found 0.088 m and 0.075 m respectively. This result may indicate that refinement of spherical harmonic geopotential model for the year 1996 with GPS/ benchmark data gave preliminary values of geoid undulations that are acceptable for practice purposes.
On the other hand, much of the current vertical control was lost due to the destruction or disruption. Because the network was not dense enough to support the use of GPS to get elevations, a precise geoid model should be determined based on a combination of gravity with GPS/ leveling.
References
Nakiboglu, S.M., Eren, K. Shedayed, A.M. (1994), Analysis of distortions in the National Geodetic Network of Saudi Arabia, Bulletin Geodesique 68, 220-229.
Martin, Daniel J. ( 2001). Implementing NGS Draft Guidelines for GPSderived Orthometric Heights. ACSM 2001 spring conference paper. Golden Software,Inc, „Surfer software version 8.02“ Briggs, I. C. (1974), Machine Contouring Using Minimum Curvature, Geophysics, 39, 39- 48.
Nakagawa, H., Wada, K., Kikkawa, T., Shimo, H., Andou, H., Kuroishi, Y., Hatanaka, Y., Shigematsu, H., Tanaka, K., and Fukuda, Y. (2003), Development of a new Japanese Geoid Model, ” GSIGEO2000”, Bulletin of the Geographical Survey Institute, Vol. 49, March.
Ghilani, Charles D., and Paul R. Wolf, (2002), Elementary Surveying an Introduction to Geomatics, 10th edition Prentice Hall, New Jersey Journel, A. G. and Huijbregts, C. J. (1978), Mining Geostatistics, Academic Press, New York, 600 p. Kitanidis, P. K. (1997), Introduction to Geostatistics, Applications in hydrogeology, Cambridge University Press, 249 p.
Martensson, S. (2002), Height Determination by GPS – Accuracy with Respect to Different Geoid Models in Sweden, FIG XXII International Congress, Washington, D. C., April 19- 26.
Sandwell, D. T. (1987), Biharmonic Spline Interpolation of GEOS- 3 and SEASAT Altimeter Data, Geophysical Research Letters, 2, 139- 142.
The paper was presented at FIG Congress 2014, Kuala Lumpur, Malaysia, 16 – 21 June 2014













 (6 votes, average: 2.50 out of 5)
(6 votes, average: 2.50 out of 5)





Leave your response!