When ellipsoidal heights will do the job, then why not use them!

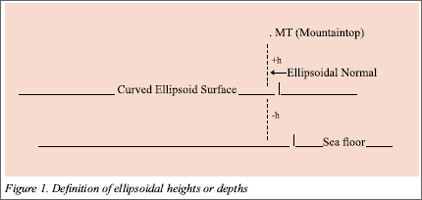
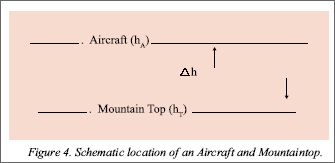
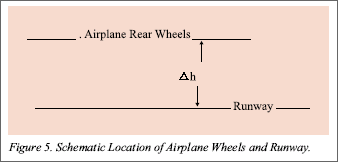
In Today’s world, with GPS, we can survey ellipsoidal heights (h) with 5-10 cm accuracy for geodetic control points on land and differential heights (?h) between well defi ned topographic features with relative accuracy of 1: 1Million or better. In few specific cases, this type of accuracy may require specially designed GPS surveys. In navigational mode, an instantaneous positional accuracy of about ± 5 m is easily possible. As these heights are the direct product of the GPS survey(s) and thus defi ned with respect to the ellipsoid, which is a time-invariant zero reference surface, they can be used without any reference to the geoid or Mean Sea Level (MSL). If we recall, in the classical surveys, e.g., triangulations and/or traverses, the vertical angles used to provide the “?h” and thus there will not be any need to convert them to orthometric heights.

Direct use of ellipsoidal heights will eliminate the need for leveling control to support topographical mapping and other non-engineering projects. This would be a major saving of time and resources.

This paper explains how ellipsoidal heights and/or depths can be used in many applications e.g., for contouring Earth’s topographic relief on maps over the entire Earth, navigating safely in open ocean, shallow waters, and in harbors avoiding grounding and overhead structures. Furthermore, the use of these heights will help to fl y clear of mountains tops and vertical obstructions with full confi dence and land on runways without bumps. Algorithm(s) or procedural steps to get the best results using “h or ?h” are also included.

Ellipsoidal Heights

Many misconceptions and confusing definitions about heights are still floating around with many users. Some of them are even taught in schools. To clarify a few important examples, the following factual statements about them are:

a. Orthometric heights, “true” and “Normal”, are not the same. Thus, treating them under “elevations” can mix up the different data sets.

b. Geoidal heights are neither elevations nor orthometric heights.

c. Mean Sea Level (MSL) is a non-equipotential surface and not equivalent or identical to the gravimetric geoid.

d. Ellipsoid is NOT the zero reference surface for either elevations or orthometric heights.

e. All the associated ellipsoids with the local and regional geodetic datums, except for the North American Datum (NAD 83) are not geocentric.

Here, it is also felt necessary to include the defi nition of the ellipsoidal heights (Figure 1).

Topographic Maps

A. Geodetic Control and Spot Heights –

Using the high accuracy global, continental, regional, and national 3-D eodetic systems, viz., WGS 84, SIRGAS 00, KGS 95, and other 3-D geocentric datums, viz., NAD 83, differential GPS surveys can easily provide the required heights at 1-2 m accuracy for topographical mapping.

B. Contouring –

Figure 2 shows a topographic scenario, which includes a hilltop “H”, building “B”, a shore point on an inland sea “I”, e.g., Caspian, a lake “L”, road crossing “R”, and stream junction “S” on a map, which is directly drawn on Earth’s ellipsoidal surface without projection. There will be no seam and discontinuity of geodetic coordinates between any two maps, adjoining or far apart. In addition, these maps will retain the true North orientation and have no practical distortion in scale and/or shape (Kumar, 2004) 1.

On the real Earth surface, a GPS survey will directly provide the ellipsoidal heights (h) of the topographic features and the differential heights (?h) between them (Figure 2). Thus, we can contour Earth’s real topographic relief with these ellipsoidal heights. There is no need to establish MSL and/or model the geoid as zero reference and compute orthometric heights. This approach will eliminate gravity survey requirement(s) towards production of topographic maps.

It is to be noted that we will not have a height anomaly for the Caspian or Dead Sea to show that they are below the sea level (?). Also, there will be no need to have a separate lake datum, e.g., the Great Lake Datum, to over come the “reality” of having different heights for any two-shore points.

Monitoring vertical movement

Just like the horizontal case, we can monitor vertical crustal movement. For land areas, ellipsoidal height changes at Benchmarks (BMs) and for the sea level at Tidal Benchmarks (TBMs), can be measured with specially designed GPS surveys. Here, a geodetic “caution” is that there should be no defi nition change in the World Geodetic System (WGS) 1984, the coordinate system used in GPS surveys. In addition, there should be no change in the position processing software during the project.

Nautical charts

A nautical chart “KChart”, like a topographical KMap, compiled and drawn with the KMap system will provide seamless coverage. Computerized digital charts can also be combined into a mosaic, which will be unfolding the real ocean underneath, to guide the ship’s captain for safe navigation along any route.

On a KChart, using the timeinvariant ellipsoidal depths of the sea floor (Refer Section on Marine Navigation below), depth contours can also be depicted. Here, the time-variant ellipsoidal heights of the sea surface, like an instant sea floor “state”, will enable the captain to monitor the clearance of the keel especially inside harbors.

Use of ellipsoidal depths for ocean areas will also ensure continuity with the land areas.

Marine Navigation

For safe marine navigation, a very important requirement is to know the exact “location” of the sea floor or its depth with respect to a zero reference surface. Time-invariant ellipsoidal depths or heights (h) of the sea floor surveyed with GPS provide such locations and when stored in a bathymetric database, they will be available for future use. Figure 3 is a schematic scenario showing the locations of overhead structure, highest mast, pilothouse, sea surface, keel, seafl oor, and the ellipsoid.

In Figure 3, the different measurements are:
DC = Ellipsoidal Height of sea floor (+h)
AC = Ellipsoidal Height of sea surface (+h)
BC = Ellipsoid Height of ship’s Keel (+h)
CE = Ellipsoidal Height of the Pilothouse (+h)
CF = Ellipsoid Height of Ship’s Mainmast (+h)
CG = Ellipsoid Height of the Overhead Structure (+h)
BD = Depth of Sea Floor from keel as measured by acoustic sounding.

During the GPS surveying, the distance BD between the ship’s keel and sea floor will be measured with presently used acoustic sounding techniques. Then, the ellipsoid height of the sea fl oor DC will be

DC = BC – BD = [CF – BF] – BD

In this configuration, the distances CF, BF, and BD are measured during GPS surveys without any reference to the stage of the tide or any tidal surface. This is the decided advantage over the time-variant bathymetric depths, determined with respect to “fluctuating” tidal surfaces. While underway,
using a mainmast-mounted GPS antenna and the ship’s general arrangement drawings, the captain of any ship can determine at any time the ellipsoid depth or height of the ship’s keel and mainmast. Combining this information with the ellipsoid depth of the sea floor, the shipboard computer can calculate the keel clearance for safe navigation independent of the tides. Similarly, knowing the ellipsoid height of overhead obstructions, vertical clearance of the mainmast can also be easily determined (Kumar and Maul, 2004).

Air navigation

A. Aeronautical Charts

Aeronautical charts, like topographic maps, can also be compiled and drawn using the no-projection mapping system (Kumar, 2004). All height information for aerodromes and vertical obstruction will be surveyed using GPS as ellipsoid height (h) in WGS 84.

B. Vertical Clearance while Navigating

Obtaining the plane’s ellipsoid height (hA) from the onboard GPS receiver and combining it with vertical obstruction height data, the pilot will be able to compute the vertical clearance “?h”. Figure 4 shows a scenario for an aircraft flying over a mountaintop. While flying over buildings and towers in cities and near aerodromes, the accuracy of “?h” can be improved with DGPS surveys. Recalling that the vertical angle surveys of the past provide “?h”, the ellipsoidal height “h” for the mountain peaks can be easily computed from the existing survey data.

C. While Landing

When descending near the aerodrome and approaching for landing, the pilot can routinely obtain with DGPS surveys the separation “?h” with accuracy of ± 5-10 cm between the plane’s rear wheels and runway for smooth landing (Figure 5).

D. Computing Shortest Distance between Aerodromes

Aerodromes are not located on the ellipsoid and thus, the geodesic will never provide the shortest distance between them. In an actual flying, a plane starts from an aerodrome “A” at height “hA”, climbs to an altitude “h”, which may vary during the flight for various reasons, then descends towards the aerodrome “B” at height “hB” and lands there. No pilot will ever be able to adhere to any mathematically computed route.

Thus, what is needed a good approximation of the shortest separation (or distance) between the starting and landing aerodromes to plan a route for saving fuel and flying time. A practical estimate for distance between two aerodromes will be the great elliptic line “GLE” (Bowring, 1984), which can be computed using the semimajor axis (a’) as under (van Gelder, 1998):

a’ = 6378137 + (hA + hB)/2

where “6378137 m” is the semi-major axis (a) of the WGS 84 Ellipsoid.

Summary

In topographic mapping, charting, navigation, vertical crustal movement monitoring, and other non-engineering applications, direct use of GPS surveyed accurate ellipsoidal heights will provide a practical, cost effective, and time saving approach. In case of vertical movement monitoring, any change in definition or the software can contaminate the data integrity.

References

Bowring, B. R., “The Direct and Inverse Solutions for the Great Elliptic Line on the Reference Ellipsoid”, Bull. Geod., 58, 1984.

Kumar, Muneendra, “A Geodetic Approach: Universal No- Projection Seamless Mapping (UNSM) System”, ACSM Journal SaLIS, Vol. 64, No. 3,
September 2004.

Kumar, Muneendra and Maul, George A., “GPS Surveyed Time- Invariant Sea Floor Depths for Safe Navigation”, GPS World (In print). van Gelder, Boudewijn H. W., 1998, Personal communication..