| Geodesy | |
Tracking satellite footprints on Earth’s surface
A coordinate transformation method to compute ECEF coordinate of a satellite revolving in Keplerian orbit in TEME coordinate |
 |
|
 |
|
Reference systems are used in Geodesy, Astronomy and Spatial information science extensively. In addition to well established systems like ICRF, MOD, TOD, and WGS84, various other systems are available that arise from intermediate or approximate transformations [6]. Computing the footprint of a revolving satellite or space object in terms of ECEF (Earth Centred Earth Fixed) coordinate on the Earth’s surface is an interesting problem. This problem has been solved by Vallado D. A. [1], and macros for equivalent transform are in MATLAB.
A key objective of this work is to develop a coordinate transformation method to compute terrestrial coordinate in a geocentric reference frame given its corresponding celestial coordinate. This is also an instance of coordinate transformation from ‘inertial’ frame of reference to a coordinate in ‘Earth Centered Earth Fixed’ frame of reference. The two line element dataset hosted by NORAD (North American Aerospace Defense Command) of all the satellites and space debris is the source of obtaining the inertial coordinate of a satellite. The ephemeris of a celestial object in TEME (True Equator Mean Equinox) coordinate system is obtained after processing TLE data. TEME is an inertial coordinate system conceptualized in space for location of satellites with respect to earth’s frame of reference. An exact operational definition of TEME coordinate system is very difficult to find in literature, but conceptually, its primary direction is related to the ‘uniform equinox’ (Seidelmann, 1992:116, and Atkinson and Sadler, 1951). The direction of the uniform equinox resides along the true equator ‘between’ the origin of the intermediate PEF (Pseudo Earth Fixed) and TOD (True of Date) frames [4].
In this paper we have proposed an algorithm which transforms TEME coordinate of celestial objects obtained from the NORAD TLE to a well defined ECEF (Earth Centered Earth Fixed) coordinate system.
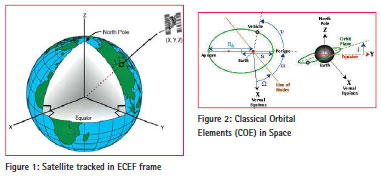
The solution obtained through this algorithm is required in many different applications such as controlling the satellite from Earth station, acquisition of remotely sensed data of a predesignated location on Earth surface, etc. The usefulness of this proposed method is very high when we want to visualize the footprint of a celestial object on a digital map in GIS environment as depicted in Figure [1].
The NORAD TLE which is maintained in the website ‘www.celestrak.com/ NORAD/elements’ mentions the classical orbital parameters of celestial objects, like satellites and debris revolving in Keplerian orbit. The orbital parameters which define the instantaneous position of the celestial objects are known as Classical Orbital Elements (COE). The COE describes the orbit in the form of these parameters given by

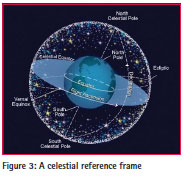
TEME coordinate system lies in celestial and inertial frame of reference Figure [3] and is based on mean equinox. TEME is not fixed to earth surface and hence does not rotate along with rotation of Earth. If we want to see the location of any celestial object on a digital map in 2D or in the surface of a digital globe in 3D, there is a coordinate system required which is fixed with Earth rotation. Therefore to visualize the footprints of a revolving celestial object around the Earth, whose instantaneous position can be specified through the TEME coordinate obtained from NORAD TLE, a coordinate transformation is required which can transform the TEME coordinate of the satellite to the ECEF coordinate of the earth. Hence the basis of this computational problem is to develop a coordinate transformation which will transform the TEME Coordinate to ECEF coordinate of the celestial object. In the next section, the explanation of TEME and ECEF coordinate is given followed by the transformation algorithm later.
The TEME coordinate system
There are two consideration of visualizing TEME (True Equator Mean Equinox) coordinate system: i) TEME of Date
ii) TEME of Epoch
i) TEME of Date: The TEMED system is a less common reference system that is aligned with the true equator and the mean equinox at the time of consideration. Its z-axis is parallel to the instantaneous rotation axis of the Earth (i.e., z-axis along the true rotation axis of the Orbit Epoch), but the x-axis points into the direction of the mean vernal equinox at the concerned time. The TEMED system arises implicitly in an orbit determination program, when true sidereal time is substituted by mean sidereal time in the transformation of measurements from the Earth- fixed frame to inertial frame. The difference between mean and true sidereal time (or likewise the difference between the mean and true equinox) amounts to roughly 15”=1s at maximum, and varies with the longitude of the Moon’s ascending node on the ecliptic. The TEMED system is for, e.g., applied in the generation of NORAD elements.[6] In this, epoch of the TEME frame is always the same as the epoch of the associated ephemeris generation time. [4]
ii) TEME of Epoch: In this system, the Z points along the true rotation axis of the Coordinate Epoch, [5] and X points toward the mean vernal equinox. The epoch of the TEME frame is held constant. [4] TEME can use both Cartesian and COE elements for representation of coordinate. [5] In COE, position and velocity can be defined by six Keplerien elements as depicted in Figure [2]

The ECEF coordinate system
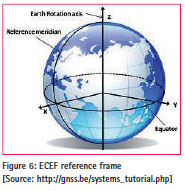
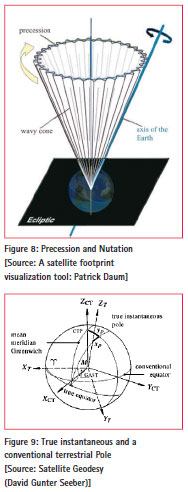
ECEF (Earth-Centered Earth-Fixed) is a Cartesian coordinate system, and is sometimes known as a ‘conventional terrestrial reference frame’ system. The origin (0, 0, 0) is defined as the center of mass of the Earth, hence the name Earth- Centered. Its axes are aligned with the International Reference Pole (IRP) and International Reference Meridian (IRM) that are fixed with respect to the surface of the Earth, hence the name Earth-Fixed.
The z-axis points towards the north but it does not coincide exactly with the instantaneous Earth rotational axis. The slight ‘wobbling’ of the rotational axis is known as polar motion. The x-axis intersects the sphere of the Earth at 0° latitude (Equator) and 0° longitude (Greenwich) Figure [6]. This means ECEF rotates with the earth and therefore, coordinates of a point fixed on the surface of the earth do not change. [7]
ECEF uses only Cartesian element for representation of position and vector [5]:

Relation between TEME and ECEF coordinate System
In defining a coordinate system, in general, we choose two quantities: the direction of one of the axes and the orientation of the other two axes in the plane perpendicular to this direction. The latter orientation is often specified by requiring one of the two remaining axes to be perpendicular to some direction. In the case of TEME and ECEF the same is followed. For transformation of ECEF from TEME, first we need to transform TEME to PEF (Pseudo Earth Fixed) Coordinate system. We will see all the coordinate systems which fall in between TEME and ECEF in a single frame shown in Figure [7]:
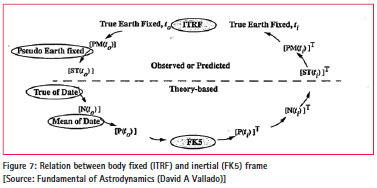
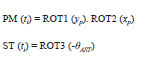
This figure depicts the transformation of a state vector in the body fixed to inertial frame. PEF (Pseudo Earth Fixed), ToD (True of Date), MoD (Mean of Date) are intermediate frames. FK5 defines the Celestial Reference Frame and ITRF defines Terrestrial Reference Frame. If we go through the FK5 to ITRF ellipse depicted in Figure [7], we will find the transformation frame through which we can solve our objective. Although in our case of TEME to ECEF we will not follow exactly what is mentioned in the Figure [7]. But it is very close.

The same relation will be used when we will process the transformation between TEME and ECEF. Because ECEF is a body fixed and TEME is a celestial coordinate system.
Solution approach
The transition from Space Fixed Inertial System (CIS) to Conventional terrestrial System (CTS) is realized through a sequence of rotation that account for:
– Precession
– Nutation
– Earth rotation including polar motion
These can be described with the matrix operations. For a point on a sphere, described through a position vector r, the equation is:

Precession and Nutation
Earth axis of rotation and its equatorial plane are not fixed in space, but rotate with respect to an inertial system. This results in some gravitational attraction of the Moon and the Sun on the equatorial bulge of the Earth. The total motion is composed of a mean secular component (Precession) and a periodic component (Nutation).[3] Corrections to the Nutation parameters ![]() supplied as Earth Orientation Parameters (EOP) from the IERS are simply added to the result. These corrections also include effects from Free Core Nutation (FCN) that correct errors in the IAU-76 precession and IAU- 80 nutation. However for TEME, these corrections do not appear to be used. [4]
supplied as Earth Orientation Parameters (EOP) from the IERS are simply added to the result. These corrections also include effects from Free Core Nutation (FCN) that correct errors in the IAU-76 precession and IAU- 80 nutation. However for TEME, these corrections do not appear to be used. [4]
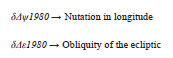
Sidereal Time
It is a measure of time defined by Earth’s diurnal rotation with respect to the vernal equinox. [8] This is responsible for most of time dependency of the vector components. This process is usually coupled with Polar Motion. It transforms the non rotating frame to a rotating coordinate system. It addresses the variability in sidereal time and requires the Greenwich Apparent Sidereal Time (GAST), because the rotating frame references the Earth’s actual equator of date, which is the true equator. GAST is measured on the true equator relative to the true equinox. And Greenwich Mean Sidereal Time is measured along the true equator relative to the mean equinox. The difference between two times is called equation of equinox. [1]
The rotation matrix is then:

Earth Rotation and Polar Motion
For the transition from an instantaneous space-fixed equatorial system to a conventional terrestrial system, we need two further parameters. They are called Earth Rotation Parameters (ERP) and Earth Orientation Parameters (EOP), namely
![]()
Unlike precession and Nutation, Earth rotation parameters cannot be described through theory but must be determined through actual observations by an international time and latitude service. The Earth Orientation Parameters (EOP) describe the irregularities of the Earth rotation with respect to a non-rotating reference frame.[9] The IERS (International Earth Rotation Services) has been maintaining these parameters from 1988.
The Earth Fixed system is realized through the conventional orientation of a cartesian (x, y, z)CT system. The zCT axis is directed towards the conventional terrestrial pole CTP, and xCT axis towards the mean Greenwich meridian. The relative position of the instantaneous true pole with respect to the conventional terrestrial pole CTP is usually described through pole coordinates xp, yp. xp, yp and describes the polar motion with respect to the crust.[9]
The polar transformation matrix is:
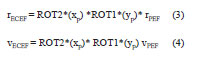
The multiplications of transformation matrix of pole coordinate xp and transformation matrix of pole coordinate
. ![]()
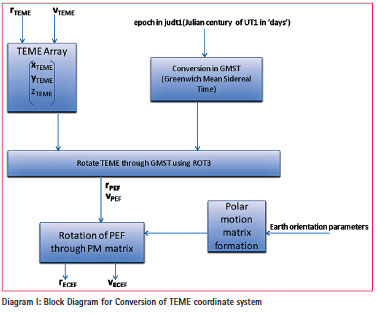
Block Diagram and Algorithm for TEME to ECEF conversion
Diagram 1 explains the process flow of coordinate transformation:
Algorithm






Step 6. Return (ECEF); // This function
is returning the ECEF ephemeris.
Step 7. [FUNCTION END].
This test is done after producing
NORAD element data set and
obtaining TEME ephemeris.
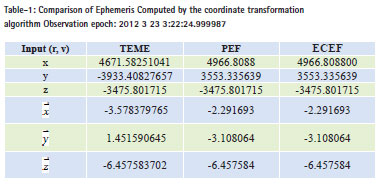
The TEME coordinates were the input in our proposed system and tabulated the observation in PEF and ECEF coordinate system.
Application & future works
The main reason behind this conversion is to visualize the moving object on a 2D map. NORAD element set was able to generate x, y, z but in unknown coordinate system, i.e. – TEME. So, we developed this conversion system which is able to convert TEME into ECEF coordinate system. This coordinate conversion will be proven very beneficial for entire GIS community, especially while working with celestial object. As far as future work is concerned, it can be further converted into geographic coordinate system (i.e., – Lat., Long., and Alt.).
Conclusion
In this paper, a method of conversion of an inertial frame to non-inertial frame has been discussed. In this case we have taken a coordinate system TEME, for which no proper definition is available. We have opted first to transform TEME to PEF coordinate system using GMST, and then transform PEF to ECEF using polar motion coefficient. In this, time conversion method has been used and polar motion parameters have been taken from the http://www.celestrak.com/SpaceData.
Acknowledgement:
A Sincere thanks due to Sir David A. Vallado, for his valuable suggestion, while working on this problem. The success of this algorithm was possible because of his insightful instructions.
References
[1] Vallado D. A., McClain Wayne D., “Fundamental of Astrodynamics and Application”, 2nd Edition, Microcosm Press: USA and Kluwer Academic Pubishers: The Netherlands, 2001.
[2] AIAA Astrodynamics Standard: Propagation Specifications, Test Cases, and Recommended Practices, American Institute of Aeronautics and Astronautics.
[3] G. Seeber, “Satellite Geodesy”, 2nd Edition, Walter de Gruyter: Germany, 2003.
[4] Vallado D. A, Crawford Paul, Hujsak Richard, Kelso T. S., “Revisiting Spacetrack Report #3”, AIAA 2006-6753.
[5] Gorman Shaun, “A Brief Introduction to Astrodynamics”, www. public.iastate.edu/~fchavez/.
[6] Montenbruck, E. Gill, Th. Terzibaschian., “Note on the BIRD ACS Reference Frames”, DLR-GSOC TN 00-01.
[7] http://en.wikipedia.org/wiki/ECEF
[8] Vallado D. A, Seago john h., “The coordinate frames of the US space object catalogs”.
[9] Bizouard Christian, Gambis Daniel, “The combined solution C04 for Earth Orientation Parameters consistent with International Terrestrial Reference Frame 2008”, Observatoire de Paris, SYRTE, 61 av. de l’Observatoire, Paris, France.














 (4 votes, average: 4.50 out of 5)
(4 votes, average: 4.50 out of 5)



Leave your response!