Towards hazards prediction

Many of the world’s volcanoes that erupt, experience significant preeruption surface deformation. Internal magma pressure makes the surface bulge upwards and outwards. Thus, precise monitoring of surface deformation has the potential to contribute significantly to the realisation of a predictive capability of volcanic eruption. In particular, eruption source depth and evolution time can be estimated from surface deformation. The scale of this deformation is typically centimetric to decimetric over tens of square kilometres and over periods of weeks. Horizontal displacements show typically a radial pattern of movement of up to 10 cm with the displacement of the vertical components in the range of 4 to 6 cm per year (Wadge et al., 2005). Furthermore, Wadge demonstrated that SAR interferometry images could be used to detect displacements of 70 to 90 mm uplift. However, data rates of typically 35 days are too slow for an early warning system.

In addition to the use of precise positioning and timing information to facilitate direct monitoring of deformation, the positioning function is vital for spatio-temporal referencing of the relevant multiple and complementary data types for volcano monitoring (e.g., seismicity, ground surface deformation, geothermal, gravity, and geomagnetic). This approach is particularly useful for enhanced risk assessment and early warning of volcanic eruptions. In architectural terms the monitoring network is an array of distributed intelligent nodes (sensor motes), consisting of low-cost, commercially available, and off-the-shelf components (as far as possible) with built-in local memory and intelligence, with self-configuration, communication, interaction and cooperative networking capabilities. The nodes should be able to identify the type, intensity, and location of the parameters being measured, and collaborate in an inter-nodal manner with each other to perform distributed sensing for event confirmation and significance. Janssen (2002) has shown that geodynamic applications such as volcano deformation monitoring, require a dense spatial coverage of sensor stations.

Although the requirement for centimetre level accuracy points to the need for GNSS carrier phase measurements, the need to keep costs down (both in terms of technical complexity and power consumption), precludes the exclusive need to build expensive carrier phase GNSS chips into all nodes (Drescher et al. 2008). Hence, a compromise scenario is to have both types of nodes, some equipped with RF (Radio Frequency) as well as carrier phase GNSS chips that are used for absolute coordinate and time referencing but the majority of nodes equipped only with RF technology for communication and inter-nodal range measurements. The limited GNSS aiding proposed here should enable RF positioning to deliver centimetre level positioning (and high accuracy timing) both in terms of error calibration and temporal synchronisation.

In this case the sensors equipped with GNSS chips calculate their positions in a higher reference frame with high accuracy, and serve as anchor (= control or reference) points for the monitoring network. The communication function of the network should enable the exchange of the data required for positioning within the monitoring network. This includes communication between the sensors, and between the RF nodes and GNSS reference stations. This should enable GNSS aiding to take place but accommodate the flexibility of allowing the RF nodes to position themselves exploiting internode distance measurements. With a high density of RF nodes, the inter-node distances between volcanic activity sensors are expected to be short thereby enhancing positioning accuracy.Such a monitoring system requires multiple key features including construction of the hardware that fulfil the requirements in terms of size, battery life and robustness, the extraction of ranges (distances) between sensor nodes, appropriate supporting network communications, protocol development, optimal routing and positioning. Currently various research activities are underway globally to study the feasibility of smart sensing for environmental applications. This study addresses specifically the position function and characterises the performance of a novel high positioning algorithm using simulated range measurements at the Sakurajima volcano in Japan.

Positioning strategy

RF positioning

Radio Frequency (RF) includes rates of oscillation within the range of about 3 Hz to 300 GHz. Recent advances in lowpower computing platforms and wireless technologies, such as personal area networks (IEEE 802.15.4) have enabled the creation of sensor platforms that are capable of operating for extended periods while using wireless communications to relay sensor data. The radio technology used in a wireless sensor is usually short range (< 50 m) and low bandwidth to maximise the operating lifetime of the wireless node once deployed. A fundamental issue in positioning using RF signals is the determination of the distance between the wireless nodes.

Those methods that estimate the distances by exploiting the RSSI (Received Signal Strength Indicator) or cell-ID are not used for deformation monitoring due to their unreliability and inaccuracy. Here, the Time of Arrival (TOA) or Time Difference of Arrival (TDOA) methods are preferred, where the time delay is used to derive the distances between nodes if there is a direct line of sight. To date there has not been a practical demonstration of the capability of any of the current approaches to deliver centimetre level positioning in a continuous and reliable manner as required for monitoring of deformation associated with volcanoes. However, research has shown that there is not much likelihood that this will be the case in the near future.

For an unmodified WLAN (Wireless Local Area Network, IEEE 802.11) the ranging techniques TOA or TDOA can hardly be used due to the lag of time synchronisation (Müller 2004). Currently, only a metreaccuracy can be achieved by using time delay measurements (Uthansakul and Uthansakul 2008). Therefore, alternative signals for the extraction of ranges between two devices should be considered. Ultra Wide Band (UWB) technology uses a pulsed, very low transmit power radio signal that provides very wide bandwidth.

UWB is defined as signal with a fractional bandwidth greater than 25% or, above 2 GHz, any signal with a bandwidth > 500 MHz. One of the key advantages of UWB, which makes it interesting for positioning applications, is the fine time resolution that can be achieved, due to its wide bandwidth. This enables very accurate measurements of time of flight, leading to highly accurate positioning (Gezici et al, 2005). It also enables resolution and elimination of the closely spaced multipath propagation. An assessment of UWB has been made by Meier and Mühlebach (2005). Ubisense offers currently a 3D positioning system stating an accuracy of 15 cm. However, the technology has the potential to deliver sub-decimetre level positioning by timeof- flight measurements. Due to these advantages, the UWB signal technique can also be considered for network positioning.

Brodin et al. (2005), use the time of flight between two Bluetooth transceivers to derive inter-node ranges. A two-way ranging technique is used to cancel the clock bias and obtain accurate range between two devices. Certain short range ultrasound based positioning systems can reach cm-level accuracy (Priyantha, 2005). However, in hazardous outdoor environments with relatively large areas and temperature ranges to cover, such methods are not practical.

A significant part of a high accuracy positioning system to support deformation monitoring is the determination of 3D coordinate positions from the estimated ranges. This paper is based on a novel positioning algorithm (explained briefly in this section) for use with high quality range measurements. The algorithm allows for the determination of network sensor node coordinates based on a set of range measurements under certain circumstances and is independent of the type of signal used.

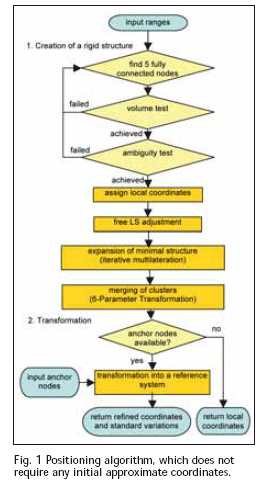
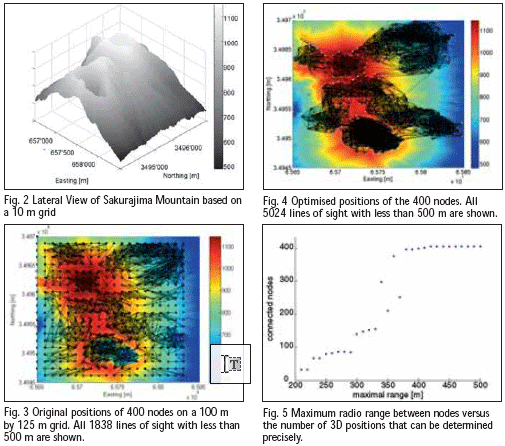
Positioning algorithm

The local 3D positioning algorithm presented in this paper takes into account the weaknesses of current wireless ad-hoc positioning methods and algorithms, including the absence of quality and integrity indicators for the positioning results and performs well even in the presence of high variances in range measurements.

The positioning strategy can be broken down into two phases: 1. Creation of a rigid structure: The key issue for anchor free positioning is to find a globally rigid graph, or in other words, a structure of nodes and ranges which has only one unique embedding, but still can be rotated, translated and reflected. In 3D, the smallest graph consists of five fully connected nodes in general position.

If such an initial cluster passes statistical tests, additional vertices are added consecutively using a verified multilateration technique. These tests include a “folding-ambiguity test” that prevents the algorithm to create false rigid structures. If, for example four nodes are in one plane, the height of that tetrahedron can not be determined well. A “volume test” eliminates those cases.

2. Transformation of the cluster(s) into a reference coordinate system: If the local cluster contains at least four vertices that are also anchor nodes in a reference system, then the cluster is eligible for a transformation into that particular coordinate system. The process flow of the overall positioning strategy is illustrated in Figure1. A more elaborate discussion of the positioning algorithm and details of the mathematical background are presented in Mautz et al. (2007).

Optimised network set up for volcano Sakurajima Sakurajima is an active volcano and a former island (now connected to the mainland) of the same name in Kagoshima Prefecture in Kyushu, Japan. It is a composite volcano with the summit split into three peaks; its highest peak rises to 1’117 metres above sea level.

The volcano is extremely active erupting almost constantly. Thousands of small explosions occur each year, throwing ash to heights of up to a few kilometres above the mountain. Monitoring of the volcano for predictions of large eruptions is particularly important due to its location in a densely populated area, with the city of Kagoshima’s 600,000 residents just a few kilometres from the volcano. Several institutions are involved in monitoring Sakurajima, including the Sakurajima Volcano Observatory (where data are captured by levelling, EDM and GPS) and Kagoshima University (which uses EDM and GPS). Additionally Landsat 7 images are analysed. However, a dense network of location aware nodes is still to be deployed. This section uses a Digital Surface Model (DSM) to simulate such a network and assesses the performance that could be achieved.

The Digital surface model The network positioning analysis is based on a 10 m by 10 m reference DSM of the central parts of volcano Sakurajima comprising an area of 2 km by 2.5 km. A 3D view of the data is shown in Figure 2. In order to establish a useful network of sensors with positional awareness for Mount Sakurajima, several scenarios were simulated and assessed. The main driver for successful positioning in a sensor network is the geometry of the network, i.e. the locations of the nodes.

Other key factors are the total number of nodes, number of anchors (i.e. reference) nodes, maximum range length and the mean error of the range measurements. Based on the positioning algorithm described in section 2, the performance of such a network can be quantified.

Such a study supports a future real network implementation in general – not in particular for Mount Sakurajima. Various simulation scenarios In a first scenario 400 nodes were deployed on a 100 m grid. The assumption was made that the radio links are restricted to a maximum of 500 m assuming the usage of omnidirectional antennas and direct line of sight for RF signals in the chosen frequency band. Since the precise TOA ranging method requires direct line of sight, all observations with obstructed views were not considered.

As a result, the network according to Figure 3 did not have the required density for positioning. In a second attempt the locations of the nodes were optimised for a maximum of line-of-sights using a heuristic global optimisation scheme, see Figure 4. The inter-nodal connectivity (i.e. the density of the network) is 3 times higher with 5024 ranges. In this case it was possible to compute the coordinates of all nodes in the network. In another experiment the radio range, i.e. the maximal range observation

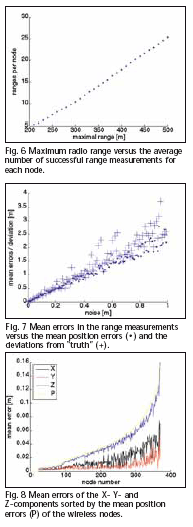
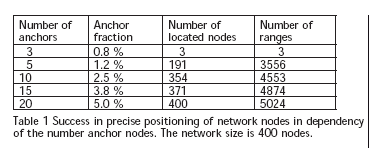
between nodes was varied in a series between 200 m and 500 m. Figure 5 shows that the critical bound is at 350 m. The number of ranges to neighbours that the average node is able to observe is directly proportional to the maximal ranging distance, see Figure 6. Another important parameter for a network configuration is the fraction of anchor nodes, i.e. the number of GPS reference stations. Results show that the minimum number for a 3D Helmert transformation of 3 reference points is not sufficient. Even the minimum number for our positioning algorithm of 5 reference stations does not mean that all nodes participate in the cluster with the anchor nodes. Deploying 5 anchors, not all nodes become part of the main cluster, see Table 1. In order to solve that problem, the number of anchors must be increased. Alternatively, the inter node connectivity can be enlarged. The most problematic parameter in wireless positioning is the ranging accuracy, since the technology of precise ranging has not yet reached the level that most applications would need. According to Figure 7, the mean error (white noise) of the range observations was varied between 0 m and 1 m. Typically, the positional errors can be expected in the size of the range errors. Other factors, such as the network density, geometry, etc. also have an influence on the position errors. Since this is a simulation, we have the opportunity to compare the results with the true positions for a network with perfect ranges. At high noise levels, the estimated errors tend to be smaller than the true deviations – this effect is caused by undetected cases of folding errors, because a wrong embedding is not sensitive to error propagation. One last observation – but nevertheless important – is that the errors of the height component are 2-3 times higher than the horizontal components, see Figure 8. This is a result of all nodes being deployed on the surface causing an unfavourable geometry for height determination.

Conclusions

This paper has shown that the implementation of a wireless deformation monitoring system is feasible if the current problem of extracting precise ranging is solved. The requirement to have direct line of sights between stations can be solved by locating the nodes for optimal directs sights. The number of required nodes depends on the transmission range. The required fraction of GNSS enabled reference nodes will be around 10%, depending on the network density.

References

Brodin, G., Cooper, J., Kemp, A., Le, T.S., Walsh, D., Ochieng, W.Y., Mautz, R. (2005): A High Accuracy Bluetooth Ranging and Positioning System, Proceedings of National Navigation Conference NAV05, The Royal Institute of Navigation, 1–3 November 2005, London.

Drescher, R., Leinen, S., Becker, M. (2008): Volcano monitoring by a GPS based hybrid sensor system, Schriftenreihe der Fachrichtung Geodäsie, TU Darmstadt, No. 28, p. 23 – 36. Gezici, S., Sahinoglu, Z., Molisch, A.F., Kobayashi, H., Poor, H.V. (2005): A Two-Step Time of Arrival Estmation Algorithm for Impulse Radio Ultra Wideband Systems. European Signal Processing Conference (EUSIPCO).

Janssen, V., Roberts, C., Rizos, C., Abidin, H.Z. (2002): Low-Cost GPS-Based Volcano Deformation Monitoring at Mt. Papandayan, Indonesia. Journal of Volcanology and Geothermal Research, 115(1-2), pp. 139–151. URL: http://www.gmat.unsw.edu.au/snap/publications/janssen_etal2002c.pdf Mautz, R., Ochieng, W.Y., Brodin, G., Kemp, A. (2007): 3D Wireless Network Localization from Inconsistent Distance Observations, Ad Hoc & Sensor Wireless Networks, Vol. 3, No. 2–3, pp. 141–170.

Meier, C., Mühlebach, M. (2005): Indoor / Outdoor Positioning with UWB, Diploma Thesis, Fachhochschule Nordwestschweiz FHA, 53 p.

Moore, D., Leonard, J., Rus, D., Teller, S. (2004): Robust distributed network localization with noisy range measurements, Proceedings of the ACM Symposium on Networked Embedded Systems.

Müller, S. (2004): Positionierung im WLAN, in: Project Work Locationbased Services for Wireless Devices, University Paderborn. Priyantha N. B. (2005): The Cricket Indoor Location System, PhD Thesis, Massachusetts Institute of Technology, 199 p.

Savvides, A., Han, C., Strivastava, M. (2001): Dynamic Fine- Grained Localization in Ad-hoc Networks of Sensors, Proceedings of ACM SIGMOBILE 2001, Italy, July 2001.

Uthansakul, P., Uthansakul, M. (2008): A Novel WLAN Positioning Technique Employing Time Delay of Successful Transmission. In: Proceedings of the 2008 the Second international Conference on Next Generation Mobile Applications, Services, and Technologies, NGMAST. IEEE Computer Society, Washington, DC, pp. 105–110.

Wadge, G., Achache, J., Ferretti, A., Francis, P.W., Morley, J., Muller, J-P., Murray, J.B., Prati, C., Rocca, F., Stevens, N.F., Upton, M. Williams, C.A. (1997): Volcano monitoring using interferometric SAR, Earthnet Online, ESA, URL: http://earth.esa.int/workshops/ers97/papers/wadge/ (accessed 3 Aug. 2009).

Acknowledgement

The authors would like to thank Kokusai Kogyo Co. Ltd., Japan for providing the reference DSM of the volcano Sakurajima.