Signal design criteria and parametric analysis

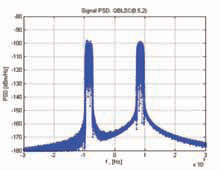
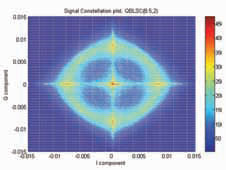
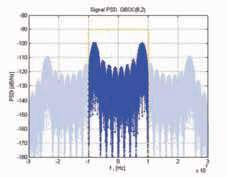
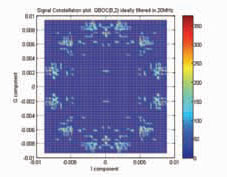
Current global navigation satellite systems (GNSSs) [1] are based on signals lying within the L-band of the radio-navigation satellite service (RNSS) spectrum. Since the need for more systems and signals is emerging, new alternative frequency resources are needed. In particular, the C-band frequency portion is envisioned as an option for future GNSSs.

Recent studies [2], focusing on comparing C-Band navigation performance with L-Band performance for global Earth coverage, have shown that C-band signals might be an interesting option in combination with L-band signals, considering forthcoming technology development. Focusing on the C-band reserved for Galileo, this is partitioned into the uplink service band (5000-5010 MHz) and the RNSS band (5010 and 5030 MHz), the latter currently unoccupied.

In addition, new aeronautical mobile (R) service (AM(R)S) are being proposed in the 5000-5010 MHz and 5010-5030 MHz bands. The analysis of compatibility issues of such AM(R)S and RNSS services calls for more specifi c defi nition of system parameters of a potential GNSS System in C-Band, especially considering the upcoming technology development in space, ground and on the receiver market envisaging in the next 10 to 15 years.

In the current phase of defi ning new navigation signals for the C-band case, it is fundamental to identify trade-off criteria and issues to deal with in the new allocated band, and then to span the possible signal options that can be adopted to exploit the available bandwidth.

With respect to signal design, in the recent past, several signal options have been introduced, ranging from new chip waveforms [3]-[5], to combining existing signals, like multiplexed binary offset carrier (MBOC) [6]. These solutions resulted in general in an improvement of the performance of the L-band services and could be used as a starting point for the defi nition of a C-Band signal.

The objective of this study is thus to compare some possible signal options on the basis of identifi ed criteria responding not just to performance improvement but also taking into account generation and emission constraints.

This paper is not meant to contain a complete and exhaustive analysis of the identifi ed options, rather it intends to anticipate possible issues to be further analysed, and/or to establish criteria to guide the selection.

In particular, it will be shown that the existing regulatory constraints of 20- Mhz band-limitation, limits considerably the possibility to improve positioning accuracy, namely, maximization of meansquared bandwidth (Gabor bandwidth, GB) of the radio signal. The idea of band-limited signals is also taken into consideration, given the strong Out of Band emission constraint in the adjacent Radio Astronomy band. As an example, in [2] a simple raised cosine (RC) pulse shape is compared with those of timelimited signals under similar conditions.

Figure 1: Signal PSD. Case QBLSC (8.5, 2).

Figure 2: Constellation plot. Case QBLSC (8.5, 2).

C-band constraints and comparison criteria for signal design

When designing signals for satellite positioning, user positioning accuracy is the main driving factor, that is directly related to time delay estimation (TDE). By using conventional parameter estimation techniques [7], such as the Cramér- Rao bound (CRB), the key factor for optimizing signals in an additive white Gaussian noise (AWGN) channel has been identifi ed in the maximization of the GB [6]. That is, the more the signal PSD is concentrated at the edge of the band, the more the accuracy is enhanced. Nevertheless, several works [1]–[6], have also shown that multipath (MP) is one of the dominant sources to the error budget, due to its random nature. As a consequence, MP mitigation has become another relevant design driver for new signal-in-space (SIS) formats. Recent studies [5] have shown that maximizing the GB bandwidth with a constraint on the autocorrelation sidelobe levels represents an effective optimization criterion for designing spreading signals with higher robustness against MP. It follows that, generally speaking, the two main issues in signal design are fulfi lled by the maximization of the GB.

When focusing on the C-band portion, a certain number of specifi c issues arises and they need to be taken into account. First of all, an intrinsic constraint is the strict allocated bandwidth (20 MHz), less than half the bandwidth available for the Galileo L-band E5 signal, that automatically limits the achievable accuracy. Moreover, differently from

the L-band portion, a new impairment becomes relevant: the level of the emissions in the adjacent band portions. To this regard, ITU [8] specifi es the maximum tolerable absolute values of power fl ux density (PFD) in the out of band regions. The requirement for the microwave landing system interference (5030-5150 MHz) allows a maximum PFD of –124,5dBW/m2 in a band of 150 kHz, while the requirement for the radioastronomy interference (4990-5000 MHz), choosing a worst case of 10 interfering satellites, allows a maximum PFD of –196.5 dBW/m2 in a bandwidth of 10 MHz. It follows that, while the requirement in the upper bandwidth is not so strict, the one in the radio-astronomy band is so stringent that the need for low out of band emissions (OOB) becomes a driving factor in defi ning new SIS for Cband. It is worth to be noticed that, to the best of our knowledge, the requirement for the C-band uplink region has not been fixed yet, but we believe it should represent a driving criterion as well.

Finally, we prefi gure that the impact of non-linearities will be another important trade-off criterion. In fact, a C-band signal needs to be transmitted at an increased power than an equivalent Lband signal due to the increased signal attenuation in the C-band region. In order to be conservative, we envision the use of a travelling wave tube amplifi ers (TWTA) that guarantees a larger gain. The drawback is the enhanced effect of non-linearities, that needs to be taken into account from the very beginning of the signal design process.

Concluding, the identifi ed criteria lead to a trade-off between two different trends in SIS design: on one hand, it would be desirable a signal with a power concentrated at the edge of the band (following the GB principle it can better perform in terms of TDE accuracy and MP robustness) and, on the other hand, it is requested a signal that has its power concentrated at the center of the band (it guarantees lower out of band emissions). This could be achieved either with bandlimited or time-limited signals, examples of which are analysed in the following.

Figure 3: Signal PSD. Case QBOC (8, 2).

Figure 4: Constellation plot. Case QBLSC (8.5, 2).

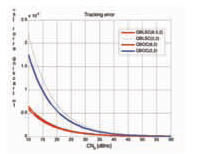
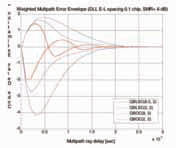
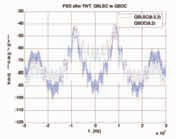
Signal definition

CQuadrature Band-Limited signals with SubCarriers (QBLSC) The band-limited signals we propose are a class of square root-raised cosine (SRRC) signals with chiprate fc and with

Fig. 5. Tracking error.

Fig. 6. Weighted multipath error envelope.

Fig. 7. PSD after TWT. QBOC(8,2) vs QBLSC(8.5,2).

sinusoidal subcarriers . This represents a simple example of bandlimitation with a high GB when is suffi ciently large. We will call this SIS, quadrature bandlimited signal with sub-carrier (QBLSC). In the following, they will be referred to hence as QBLSC(n,m), with the two parameters n and m such that

The complex envelope is of the form:

where and are two band-limited modulated waveforms

defined as

wherecosine, s = sine) are two orthogonal binary code sequences with length L; andis the band-limited SRRC pulse shape with roll-off factor and bandwidth

For the moment, no assumptions on the services and the type of spreading of navigation data are made, but we focus only on a pilot signal of the form:

Once the code sequences are defi ned, the pilot is a deterministic signal, given by the periodic repetition of the elementary signal

with period equal to

The power spectral density (PSD) of is of course discrete with line amplitudes also depending on the Fourier transform of the auto- and cross- correlation functions of the sequences

In particular if the (deterministic) crosscorrelation of the two sequences is non zero, the PSD is asymmetric w.r.t. the centre of the transmission band [9], as in Fig. 1. Here, the spectrum is given by two main lobes located at with a bandwidth of 2.4 MHz when

The periodic signal has line spectra at the multiples of the fundamental frequency

Using the standard two long sequences of Galileo E5 signals (L=10230),

Similar considerations can be properly done for each couple thus parameterizing the performance w.r.t. the spectral occupancy of the signal within the given C-bandwidth. Figure 2 describes the I/Q “constellation” plot of the QBLSC signal for a high ratio. The constellation is symmetric and presents fi ve “high density” spots, as can be easily derived from the signal in the time domain. The fi ve “high density” spots are dipped in a crown of “medium density” points that corresponds to the slow signal transitions. Each transmitted symbol is determined by the order the spots are covered during one

Filtered Quadrature Binary Offset Carrier (QBOC)

In order to make a fair analysis, we compare the QBLSC signals with a binary offset carrier (BOC) signals with similar spectral occupancy within the 20 MHz C-Band and comparable envelope construction. We address this as quadrature BOC (QBOC) signals.

The QBOC(m,n) signal is of the type:

where

The are given by the modulation of the BOCx (c = cosine, s = sine) signals, respectively, and of the two binary code sequences used for the QBLSC signals. The BOCx(m,n) are the usual square-wave subcarriers defi ned as in [6], with reference frequency fref = 1 MHz. To meet the C-band constraint, we also adopt a low-pass fi ltering of the QBLSC signal, as in Fig. 3. Figure 4 depicts the constellation plot of the (ideally fi ltered) QBOC signal for a high fsc/fc ratio. The constellation is asymmetric w.r.t. real and imaginary components. 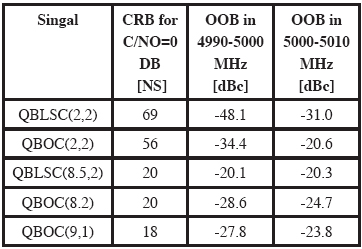The C-band fi lter cuts off differently the spectral components

Table I: Summary of out-of-band emission and tracking error.

of the two I/Q components of the QBOC signal: the BOCs has more energy between the two main lobes than the BOCc, so its spectral components are better preserved.

Numerical results

A comparison between different QBLSCs and QBOCs has been performed with respect to the identifi ed trade-off criteria. A mix of theoretical analysis and simulation was used to derive our performance results.

In terms of tracking performance and robustness against MP, we can observe from Figs. 5-6 that both the classes of signals follow the GB principle, as expected. Figure 5 represents the tracking error as a function of the signal to noise ratio, whereas Fig. 6 plots the weighted MP error envelope [10] on the benchmark two-ray channel. In the weighted MP error envelope, the classical MP error envelope is scaled according to a typical exponential distribution of the path delay of the second ray. From the GB principle it follows that, as the power spectrum of the signal concentrates to the edges of the band, the CRB decreases and the robustness against MP increases. When comparing the two classes of signals for the same configurations, performance are equivalent as long as the occupied bandwidth is equivalent. It is worth noticing that the bandwidth (BW) for the analysed QBOC is always limited to BW=20 MHz, whereas the QBLSC is intrinsically limited by the choice of the fsc, therefore for confi gurations with small / BW the QBOC allows more energy to be put at the edge of the band.

All the signals above are amplifi ed by an highly non-linear high power amplifier (HPA) at a radio frequency. The regrowth of the sidelobes of the spectrum thus become an issue. . In terms of the effect of non-linearities and out of band emissions, the performance has been analysed assuming a Travelling Wave Tube Amplifi er (TWTA) working at saturation, and measuring the level of power over the band with respect to the carrier (dBc)

The out of band emission between 4990 and 5000 MHz band are mostly defi ned by the non linear characteristics of the TWT curve, so the band-limiting is not really an advantage because of the inevitable re-growth, as depicted in Table I.

Conclusions

Some important conclusion can be drawn. Without strong output filtering it is impossible to limit the emissions for any signal to the required level between 4990 and 5000 MHz. Feasibility/complexity analysis of the needed output fi ltering will be a key point to be examined during the payload design. Depending upon the absolute value of satellite EIRP required to achieve a given C/N0 threshold, the outof- band emissions in the Radio Astronomy Band may cause levels of power fl ux density on-ground in excess of ITU limits. Proper output fi ltering shall then be made to protect such band. Other more complex generation schemes could be used to limit the emissions in the case of the QBLSC (spectrum asymmetry, non binary codes etc.). More diffi cult will be for the QBOC to accommodate these type of changes. Band limiting could be an advantage for the adjacent band emissions, spectrum which is currently allocated to the uplink for which the requirement will come from the spacecraft design. Depending on how much these emissions prove to be a constraint in the link budget, it will be diffi cult to fi lter and to generate unwanted spurious peaks in these bands. Spurious could be limited by using a linearised version of the TWT (LTWT), solution that has shown to produce reduction of 5 dB in average of emissions w.r.t. the TWT at the same input power.

Table I summarises the results for different signal confi gurations. As expected, performance is mostly driven by the position of the main lobes in the dedicated band. The actual generation mode of the signal (intrinsic or a-posteriori bandlimitation) appears to have a secondary impact on performance although SRRC baseband shaping is much more hardware friendly than generating square pulses followed by a brick-wall analogue filter.

Acknowledgements

The authors acknowledge the many fruitful discussions on the topic of the paper with R. De Gaudenzi and J.L. Gerner from the European Space Agency.

References

[1] B. W. Parkinson, J. J. Spilker, Global positioning system: Theory and applications. Washington DC, USA: American Inst. Aeronautics, 1996.

[2] G.W. Hein et al., “Envisioning a Future GNSS System of Systems – part 3,” Inside GNSS, pp. 64-73, June 2007.

[3] L. Giugno and M. Luise, “Optimum pulse shaping for delay estimation in satellite positioning,” in Proc. European Signal Processing

Conference (EUSIPCO), Antalya, Turkey, 2005.

[4] F. Antreich and J. A. Nossek,“Minimization of the tracking error in a GNSS receiver,” in Proc. ESA Workshop on Satellite Navigation User Equipment Technologies (NAVITEC), Noordwijk, The Netherlands, 2006.

[5] F. Zanier, G. Bacci, M. Luise, “Nonbinary spread spectrum signals with good delaytracking features for satellite positioning,” in Proc. Int. Waveform Diversity and Design Conference (WDD), Pisa, Italy, 2007.

[6] G. W. Hein et al., “MBOC: The new optimized spreading modulation

recommended for GALILEO L1 OS and GPS L1C,” in Proc. IEEE Positioning, Location and Navigation Symposium (PLANS), San Diego, CA, USA, 2006.

[7] S. M. Kay, Fundamentals of statistical signal processing: Estimation theory, Prentice- Hall, Englewood Cliffs, NJ, USA, 1993.

[8] ITU Radio Regulations ITU RR, Art.5, http://www.itu.int/pub/R-REG-RR/en

[9] F.Zanier, M.Crisci, “Input to the Cband study. Contribution to the signal defi nition,” ESA internal report, TEC-ETN, Sep. 2007.

[10] M. Irsigler et al., “Criteria for GNSS multipath performance assessment,” in Proc. Int. Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS), Long Beach, CA, USA, 2005.