| GNSS | |
Robust Signal Processing for GNSS
Robust statistical approaches can signifi cantly improve the performance of GNSS receivers in the
|
 |
|
Digital signal processing plays a fundamental role in any Global Navigation Satellite System (GNSS) receiver: the presence of GNSS signals is detected and the signal parameters are estimated by the acquisition and tracking blocks, the main signal processing stages of a GNSS receiver. Standard acquisition and tracking algorithms are designed under the hypothesis that the noise affecting the input samples provided by the receiver front-end is Gaussian. This assumption leads to a non-linear Least Squares (LS) problem where GNSS signal parameters are estimated by minimizing a quadratic cost function.
GNSS signal reception can however be affected by several impairments such as multipath and interference. Under such circumstances, the Gaussian assumption may fail. Jamming is a special type of interference where powerful signals are broadcast in the GNSS frequency bands with the ultimate goal of preventing GNSS signal reception. A common approach to mitigate the impact of interference is to apply the Interference Cancellation (IC) principle: the interfering signal is at first estimated and then removed from the received samples. However, a model for the interfering signal is required and imprecise a-priori information can significantly degrade the performance of IC mitigation approaches.
During the last decades, significant interest has been devoted to robust statistical approaches and robust signal processing schemes. In this context, a technique is considered robust if it is able to effectively deal with model uncertainties and model mismatches.
Several approaches exist to design robust processing schemes where the assumption of Gaussian input noise is relaxed and the LS principle is replaced by less sensitive criteria, such as the minmax approach where the worst-case scenario is considered.
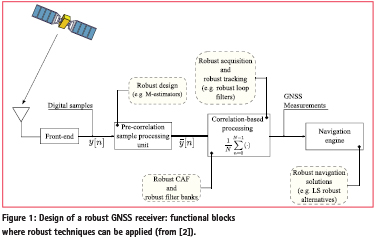
Robust signal processing techniques have the potential to significantly improve the performance of GNSS receivers in the presence of non-Gaussian phenomena and can be implemented at almost every stage of a GNSS receiver. This fact is illustrated in Figure 1 that briefly reviews the different receiver stages that can benefit from robust approaches. Despite their wide applicability to GNSS receiver design, the usage of robust approaches has been quite limited. Robust techniques have been recently considered for the computation of the user position from raw GNSS observables [1]. These approaches [1] provide significant performance improvements in the presence of multipath errors and outliers in the pseudo-range measurements.
Robust signal processing at the sample level can provide significant resilience to interference and improve receiver performance. We review and discuss two general approaches recently proposed for the design of robust acquisition and tracking schemes [2]. We show that robust techniques can provide an effective alternative to traditional IC approaches without requiring a good knowledge of the interfering term. The validity of the approaches proposed is demonstrated using the data collected during the Slovenian experiment described in a previous issue of Coordinates [3].
Classical GNSS signal processing
Standard GNSS signal processing is based on the assumption that the samples provided by the receiver front-end are affected by Additive White Gaussian Noise (AWGN). The Gaussian (or Normal) hypothesis naturally leads to a LS problem. In particular, one of the main goals of acquisition and tracking is to estimate the


is the Cross-Ambiguity Function (CAF), which is usually evaluated using a bank of correlators. Note that ( 2 ) does not depend on the signal amplitude, A, which will be independently estimated, for example, for the evaluation of the Carrier-to-Noise spectral density power ratio (C/N0), one of the main GNSS signal quality indicators.
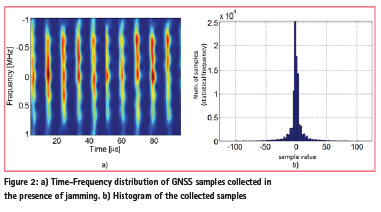
The processing described here is optimal when the model assumptions are fulfilled, i.e., when the input samples are affected by Gaussian noise. This type of processing, however, fails in the presence of model mismatches as those described in Figure 2. The figure provides the Time-Frequency distribution and the histogram of the GNSS samples collected during the Slovenian test campaign described in [3]. The input samples are corrupted by a jamming signal that periodically enters and exits the receiver input bandwidth. The presence of pulsed jamming alters the distribution of the input samples and the Gaussian assumption is no longer valid: under these circumstances, standard receivers are unable to operate.
Robust statistics and GNSS
Robust statistical methods have been developed to deal with situations where deviations from the design model may occur and render classical approaches ineffective [5-6].
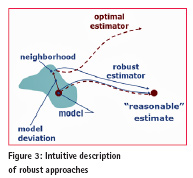
The main idea behind robust statistical methods is illustrated in Figure 3: a robust estimator shall be able to provide reasonable estimates even in the presence of model deviations.
Several approaches exist for the design of robust techniques [6], which are less sensitive to model mismatches than the optimal approaches based on the Gaussian hypothesis. These approaches are generally obtained by considering heavy-tailed noise processes whose distributions better describe situations like the one depicted in Figure 2.
Two approaches are considered here and are both based on the M-estimator framework [6]. The main idea of the M-estimator paradigm proposed by Huber [6] is that LS problem (1) can be generalized as
![]()
where the squares have been replaced by , a less rapidly increasing function of the residuals. In this case, is a positive function of complex argument that is zero only if its argument is zero. The idea is that will de-weight the impact of residuals with a too large magnitude. A possible way to design is to consider heavy-tailed random processes and set
![]()
where f(z) is the probability density function (pdf) of the input noise. The reader can readily verify that the original LS problem is obtained when f(z) is the Gaussian pdf.
Distributions with tails heavier than the Gaussian pdf are the Laplace and Cauchy pdfs defined as
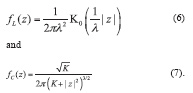
In (6), is the modified Bessel function of the second kind and of order zero and λ is a scale parameters. In (7), K is the so called linearity parameter and controls the decay of the tails of the Cauchy distribution. It is noted that the input GNSS samples, y[n], are assumed to be complex valued and thus (6) and (7) should be interpreted as bi-variate joint distributions where z is a complex variable.
The generalization of the LS problem considered in (4) leads, in general, to complex minimization problems. A possible solution is to assume that the GNSS signal amplitude, A, is small and to approximate (4) with its Taylor series expansion. In this way, a robust equivalent of (2) and (3) is obtained (see [2] for mathematical details):

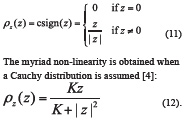
Eq.(12) has been obtained by normalizing the derivative defined in (10) in order to make converge to the identity for large values of K.
It is important to note that the nonlinearities considered here are always proportional to the input variable, z, and that only the amplitude of the input samples is affected. The phase of the samples is preserved and only the signal amplitude is attenuated.
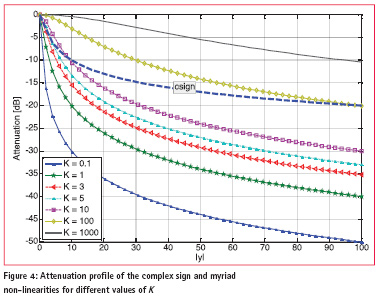
The attenuation profile for the complex sign and myriad non-linearities are provided in Figure 4. In general, the attenuation increases with the amplitude of the input samples: the larger the amplitude of the input sample, the higher the attenuation provided by the non-linearity.
Pulse Blanking (PB), a technique widely used for interference mitigation [7] can also be inscribed in the paradigm described here where does not derive from a pdf and it is given by
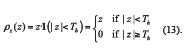
1(.) denotes the indicator function which is equal to 1 only if its argument is true and it is zero otherwise. Th, is the blanking threshold.
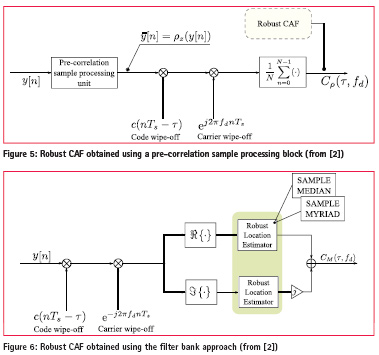
The results exposed above lead to the processing scheme depicted in Figure 5. Finally, the robust CAF can be interpreted as a form of Locally Optimum (LO) detector/generalized correlator [8], which is obtained by tackling the problem from a detection perspective.
A second approach to introduce robustness to the standard signal processing blocks of a GNSS receiver is to act directly on the filter bank (correlator) structure of acquisition and tracking. In particular, the mean performed in ( 3 ) can be replaced by robust alternatives such as the sample median and the sample myriad operators [9]. The myriad is a location estimator that is obtained when a Cauchy distribution is considered. As for the myriad non-linearity defined in (12), it depends on the linearity parameter, K. In the next section, K will be fixed to the value determined in [4]. Using these considerations, the processing scheme depicted in Figure 6 is obtained.
Experimental results
In order to illustrate the potential of robust signal processing techniques for the acquisition and tracking of GNSS signals, the data collected during the Slovenian experiment [3] are considered here. As described in [3], a car, equipped with a u-blox reference receiver and a Realtek RTL2832u device used as a Software Defined Radio (SDR) frontend, was periodically passing in front of a jammer placed on the side of the road. Although the data collected with the RTL2832u device were mainly intended for the design of jammer detectors, they can also be used to empirically evaluate the potential of the robust techniques discussed above.
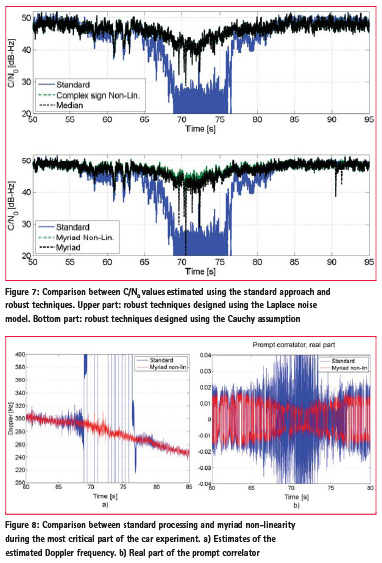
In the close proximity of the jammer, i.e. for a distance of about 5 metres, the interfering power was so strong that the u-blox receiver was not able to operate. The standard approaches discussed in Section 2, are also unable to detect and track useful GNSS signals from the data collected with the RTL2832u device. This fact is illustrated in Figure 7 that provides the C/N0 values estimated using different approaches. In the [60 – 80] s interval, the car is sufficiently close to the jammer to suffer performance degradations. In the middle of such interval, the jamming power is so strong that the standard approach is unable to track and reacquire the signal. This fact is reflected by the C/N0 values shown in Figure 7.
Robust approaches enable receiver operations even in the close proximity of the jammer and signal tracking is maintained during the whole duration of the experiment. The upper part of Figure 7 considers the case where robust tracking is implemented considering a Laplace noise. The complex sign and the median filter bank lead to the same C/N0 values.
Robust techniques obtained under the Cauchy assumption are considered in the bottom part of Figure 7. Among all the techniques considered, the myriad non-linearity provides the best performance. The computation of the myriad correlation requires an iterative, computationally demanding procedure and the loss of performance with respect to the myriad non-linearity may be due to an incomplete convergence of the algorithm. In general, the filter bank approach is more computationally demanding and pre-processing the input samples using a memory-less nonlinearity seems a preferable solution.
Since the myriad non-linearity provides the best performance, it is further analysed in Figure 8. During the most critical part of the experiment, i.e. in the close proximity of the jammer, the myriad nonlinearity allows the receiver to maintain frequency and phase lock. The estimated Doppler frequency is shown in Figure 8 a): when the myriad non-linearity is used, the receiver is able to provide reasonable Doppler estimates during the whole duration of the experiment. The right part of Figure 8 shows the real part of the prompt correlator which is used to estimate the navigation bits. Also in this case, the myriad non-linearity allows proper receiver operations and the bits can be effectively estimated from the prompt correlator.
These results show the advantages and the potential of robust signal processing for GNSS.
Conclusions
Robust signal processing techniques have the potential of significantly improving the receiver performance in the presence of model mismatches. Two approaches, based on the M-estimators framework, have been analysed in the paper: both techniques allow the receiver to operate in the presence of jamming. The first approach considered uses a non-linearity to de-weight the impact of samples with abnormally large amplitudes. These samples are, in practice, considered outliers and thus their amplitude is significantly reduced by the non-linearity. This approach has a complexity that scales linearly with the number of input samples. The second approach operates at the correlation level: robust operators, such as the sample median and the sample myriad, replace the sample mean performed by standard techniques. Although, also in this case, a significant performance improvement is observed, this second approach is more computationally demanding. The experimental results presented show the benefits of robust techniques whose usage should be considered also for the design of other receiver stages such as the filters of the tracking loops.
References
[1] Zair S., Hgarat-Mascle S. L. and Seignez, E. “A-contrario modelling for robust localization using raw GNSS data”. IEEE Trans. Intell. Transp. Syst., May 2016, 17, (5), pp. 1354–1367.
[2] Borio D., “Robust Signal Processing for GNSS”, Proc. of the European Navigation Conference (ENC), pp. 1-9, Lausanne, Switzerland, 9-12 May 2017.
[3] Baldini G., Bazec M., Blantnik A., Borio D., Dimc F., Gaberc N., Gioia C. and Stern A. “Trapping the Jammer: the Slovenian Experiment” Coordinates, Volume XII, pp. 12-18, Oct. 2016
[4] Borio D., “Myriad non-linearity for GNSS robust signal processing,” IET Radar, Sonar & Navigation, pp. 1–22, Mar. 2017, accepted for publication. On-line first http:// digital-library.theiet.org/content/ journals/10.1049/iet-rsn.2016.0610
[5] Ronchetti E. “The historical development of robust statistics”, Proc. of the 7th International Conference on Teaching Statistics, Salvador Bahia, Brazil, pp. 1-4, 2006
[6] Huber P.J. and Ronchetti, E. “Robust Statistics” Wiley Probability and Statistics. John Wiley and Sons, March 2009, 2nd edition
[7] Borio D., “Swept GNSS jamming mitigation through pulse blanking,” in Proc. of the European Navigation Conference (ENC), May 2016, pp. 1–8.
[8] Miller, J. and Thomas, J. “Detectors for discrete-time signals in non-Gaussian noise”. IEEE Trans. Inf. Theory, March 1972, 18, (2), pp. 241–250.
[9] Arce G. R., “Nonlinear Signal Processing: A Statistical Approach,” Wiley-Interscience, Nov. 2004.











 (No Ratings Yet)
(No Ratings Yet)






Leave your response!