| Positioning | |
Multisystem real time precise-point-positioning
PPP is becoming an alternative for precise positioning even in real time applications |
|
 |
|
|||||
 |
|
|||||
 |
|
|||||
 |
|
|||||
 |
|
|||||
Nowadays, a growing number of GNSS users demand highly-accurate positioning with minimal latency. PPP is a new positioning technique providing centimeter-level error. Precise Point Positioning (PPP) processes measurements from a single user receiver, using detailed physical models and corrections, and precise GNSS orbit and clock products computed beforehand. PPP differs from other precise-positioning approaches like Real Time Kinematic (RTK) in that no reference stations are needed in the vicinity of the user. Another advantage is that since the GNSS orbit and clock products are by nature global, the PPP solutions are also global. However, it should be noted that it is possible to set up a regional PPP service using a regional network of stations.
A PPP solution requires some time to converge due to the need for properly estimating phase ambiguities, but the use of combined GLONASS and GPS measurements leads to significantly better results when the observation time is short. For the GNSS user, this means that up to 18 GPS+GLONASS satellites can be simultaneously visible in open-sky areas, which represents an increase of around 60% in satellite availability compared to the GPS-only scenario. This will lead to higher accuracy and faster convergence in precise positioning applications.
A further improvement will be obtained in the near future thanks to the deployment of new regional systems in geosynchronous orbits. With these systems, the convergence time or the accuracy on a short observation time would remain unaffected, but the accuracy on applications that can afford a long observation time will be significantly improved. To achieve this, it is important to be able to compute accurate geosynchronous orbits; this is currently a challenge, but appears to be feasible in the near future.
MAGICPPP description
The PPP algorithm uses as input code and phase observations from a dual-frequency receiver, and precise satellite orbits and clocks, in order to calculate precise receiver coordinates and clock. The observations coming from all the satellites are processed together in a filter that solves for the different unknowns, namely the receiver coordinates, the receiver clock, the zenith tropospheric delay and the phase ambiguities.
The accuracy of the satellite clocks and orbits is one of the most important factors affecting the quality of the PPP. Another relevant factor that affects the PPP performances is the amount and quality of the observations. For instance, more satellites in view improve the observability of the zenith tropospheric delay. Therefore, a possible way to increase the reliability of this technique is to process GPS and GLONASS observations together.
Given that PPP is not a differential technique, it cannot resolve carrier phase ambiguities and they need to be estimated with the aid of the code measurements. This fact makes the convergence period longer than in other techniques (RTK, for instance). The generation of precise satellite orbits and clocks in real time becomes a major challenge for enabling a real time positioning service. GMV has developed an infrastructure for the generation of highly precise GPS, GLONASS and Galileo orbits and clocks in real time.
magicGNSS is a web-based suite of GNSS algorithms and products developed by GMV are available at magicgnss.gmv.com. It includes a state of the art PPP module, able to compute precise positioning for static and dynamic users in real time. In addition to the web application, an e-mail based PPP service is also provided.
Fig. 1: magicGNSS product suite
The accuracy of the PPP solution (vs. IGS) is around 1 cm, both for GPS and GPS+GLONASS, for 1-day-long observation times.
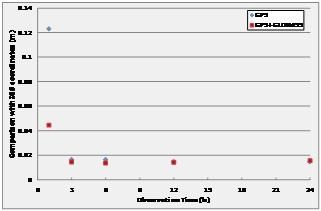
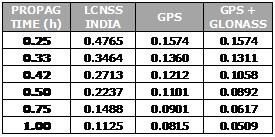
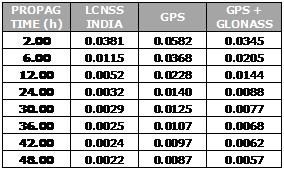
PPP with 1-hour-long observation time performances, are usually below 10 cm, and quite often below 6 cm. An observation time of 24 hours is adequate for a high accuracy post-processing solution, but is not very suited to field measurement, where shorter measurement intervals would be more practical. Fig. 2 shows the performances of Static PPP of one IGS station selected as test user (GLSV), for different observation times ranging from 1 to 24 hours. The results for GPS-only and GPS+GLONASS are shown together for comparison. It can be clearly seen that there is a benefit from longer observation times with a significant improvement after 3 hours. For 1-hour observation time, there is also a significant improvement coming from the multisystem configuration.
Fig. 2: Static PPP Performances at GLSV
These performances present multi-system PPP as an interesting option for precise positioning, since sub-dm accuracy can be reached with one hour observation time. The latency with which the solution can be obtained depends only on the latency of the reference products. Real-time generation of products implies that the solution is available immediately after the collection of the measurements.
The main application of real-time PPP, however, is kinematic positioning. In order to evaluate the performances, a receiver was installed on the roof of a van, and data were recorded during a 30-min drive in the countryside near GMV premises, illustrated in Fig. 3.
Fig. 3: Test route for kinematic PPP
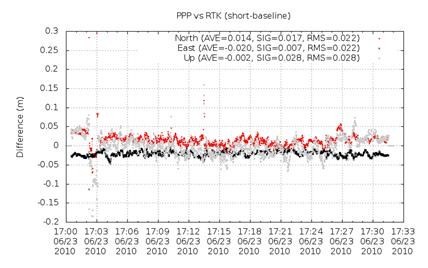
GPS data were then processed off-line with the new kinematic PPP and compared with a reference trajectory. This reference path was calculated with RTK, using a reference station installed a few km away. The difference between the solutions versus time is shown in Fig. 4.
Fig. 4: Kinematic PPP vs RTK solutions
The results match up to a few cm. Additional tests in more challenging visibility conditions and with other type of users (e.g. flight trajectories) are currently on-going, with very promising results as well. It is expected that the addition of GLONASS will improve the performances in more challenging visibility conditions.
Regional PPP
A PPP service is normally a global service, considering that the orbit and clock products are themselves global. This is true as long as the tracking stations used for the computation of the products are distributed worldwide. In this case, there is good visibility of the satellites along all their orbits, and the accuracy of the orbit and clock estimations does not depend on the location. This may pose some limitations as there are mainly two options:
1. To deploy a global network of stations, this may be complex and expensive to operate for a regional service provider
2. To relay on an external orbit and clock provider, this may limit accuracy, real time capabilities and multisystem approaches
GMV has overcome this problem as magicGNSS is able to compute their own orbit and clock products using a regional network of stations. In this case, the accuracy of the orbits and clocks is slightly degraded but this degradation occurs mainly outside the area where the stations are deployed. Inside this region, the combination of orbit and clock products is such that the positioning performances are good. Indeed, it is possible to achieve positioning performances at the same level as with a global network. This opens very interesting possibilities to regions already operating networks of GNSS receivers (e.g. for RTK), as they can deploy a PPP service using their own resources. Such service could complement RTK for areas far away from any of the base stations requiring much less stations than a classical RTK approach for the same level of precision.
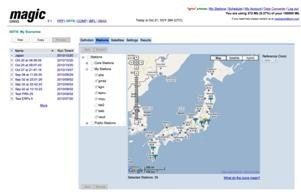
In order to demonstrate this concept some tests have been performed over different regions. The following example illustrates the PPP performances that can be achieved using a regional network of only seven stations over a relatively small country like Japan.
Fig. 5: Network of stations in Japan and differences between the coordinates estimated using products computed with the regional network and global IGS orbits
It can be observed that PPP solutions based on regional networks, even for small regions, are as accurate as PPP solutions using global networks. This opens new ways for providing precise positioning services at regional basis.
PPP performances with regional navigation satellite systems
In order to evaluate the PPP performances that can be achieved with regional navigation satellite systems, a simulation tool has been developed based on the analysis of the covariance of the PPP associated processes. It is an evolution of the covariance tool developed for analyzing OD&TS processes, described in Reference [1]. The PPP simulation tool has been validated and calibrated by comparing the simulated results with PPP results in real GPS and GLONASS scenarios obtained with the magicGNSS PPP service, see Reference [2].
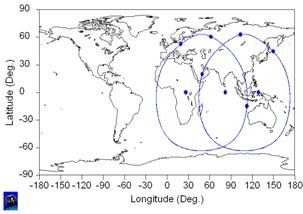
The regional navigation constellation that has been used as an example for analyzing the PPP achievable performances is a LCNSS (Low Cost Navigation Satellite System, see Reference [3]) constellation with 9 satellites, 3 geostationary satellites in longitudes 24.5º E, 82.1º E and 128.8º E, and 6 satellites in geosynchronous eccentric inclined orbits, in 3 different orbital planes, optimized for maximizing the navigation performances over India. The inclination has been set to 63.4º, and the eccentricity to 0.6. The ground tracks of the constellation satellites have been plotted in Fig. 6 below.
Fig. 6: Regional Navigation Constellation Ground Tracks
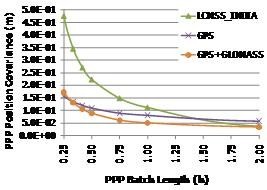
The simulated PPP performances that can be achieved over India have been plotted in Fig. 7 below. For comparison purposes, analog GPS and GPS+GLONASS PPP performances are also shown. It can be observed that the PPP performances for the regional constellation are not excellent, particularly if the PPP batch length is short, but they significantly improve as the PPP batch length increases. For 2-hour-long batch length scenarios, the regional constellation PPP performances have reached those provided by the GPS+GLONASS combined constellations. For longer batches, the regional constellation PPP performances keep on improving, reaching a very good performance level, about four times better than GPS for batches between 12 and 48 hours long.
Fig. 7: PPP Simulated Performances in meters
This apparently surprising result, can be justified considering the following two facts: first, with the regional navigation constellation alone, it is difficult to estimate the tropospheric zenith delay for time periods shorter than 2-4 hours, and second, due to good visibility conditions of the considered regional navigation constellation, the station-satellite passes are relatively long, and thus, the ambiguity resolution is more accurate than for the GNSS satellites, especially for long batches.
This means that regional navigation constellations can be used for some PPP purposes, such as scientific applications, which demand high precision, but in which the convergence time is not the most stringent requirement.
Precise orbit determination for satellites in geosynchronous orbits
Regional navigation systems are providing excellent performances for applications requiring extreme accuracy. This would only be possible if very precise orbits could be computed. Regional navigation systems are based on geosynchronous orbits, either inclined or equatorial. The computation of precise orbits for satellites in geosynchronous inclined orbits can be done by using classical methods, based on the use of the navigation signal and ground stations. It is more complex to compute precise orbits for geostationary satellites. The relative geometry between the geostationary satellites and the ground stations does not change, which makes it very difficult to discriminate any bias that may be present in the measurements leading to high correlations between orbital parameters and measurement biases or clock parameters.
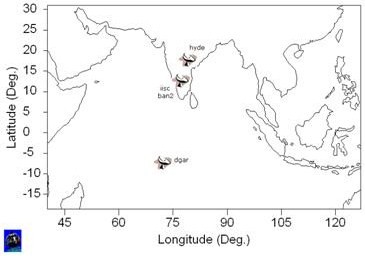
A simulation tool validated with real data has been used to assess the orbit determination accuracy that can be achieved for each of the satellites in the constellation, see Reference [1]. The same 9 satellites regional constellation optimised over India introduced in the previous section and the 4 stations tracking network depicted in Fig. 8 below have been used for this orbit determination accuracy analysis.
Fig. 8: Tracking Network (4 stations)
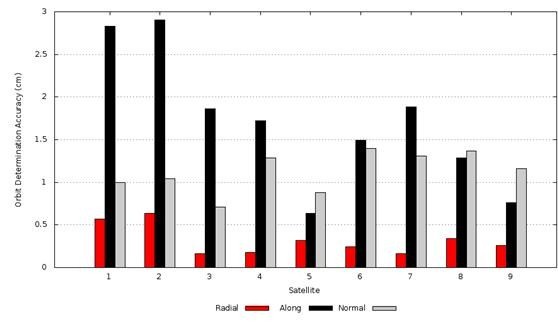
The achieved orbit determination accuracy is represented in Fig. 9 below. Satellites 1, 2 and 3 are geostationary satellites, and the rest are all in geosynchronous, eccentric, inclined orbits (GEIO).
Fig. 9: Orbit determination accuracy for the nine satellites in the constellation. Satellites 1, 2 and 3 are geostationary satellites
It can be observed that the orbits of the geostationary satellites cannot be computed with the same accuracy as the GPS or GLONASS orbits or even with the same accuracy as the orbits of the geosynchronous satellites in inclined orbits.
The only way to improve the OD&TS process for the geostationary and geosynchronous satellites is by improving the tracking geometry. This may be done by taking benefit of the eccentricity of the satellites in inclined orbits, and consequently by using measurements between the satellites. To do that it will be assumed that the satellites are emitting a navigation signal with a transmitter located in the side facing to the Earth, and that the satellites are also equipped with a navigation receiver placed on the side facing opposite to the Earth. A tracking visibility of 180 degrees has been assumed for both, transmitter and receiver. It shall be noted that for this analysis only geometrical considerations have been taken into account. A more detailed analysis is needed to analyse the impact on the satellite, receiver and payload design.
Fig. 10 bellow illustrates the OD&TS accuracy that could be achieved by using only four ground tracking stations (as depicted in map in Fig.8) together with inter satellite ranging measurements:
Fig. 10: Orbit determination accuracy for the seven satellites in the constellation. Satellites 1,2,3 are geostationary satellites
It can be concluded that it is feasible to compute very accurate orbits (a few centimeters) and clocks for all the satellites in the constellation. This is possible thanks to the use of inter satellite ranging using the navigation signal and consequently minimizing the complexity of the overall system.
One of the main advantages of the proposed approach is the reduced number of ground stations required; in this analysis only four of them have been used. It is important to notice that due to the regional character of the constellation there are some locations from where it may be possible to have all satellites in view during certain time periods. This opens new possibilities for computing real time navigation message parameters.
Conclusions
• PPP is becoming an alternative for precise positioning even in real time applications.
• GMV has developed magicPPP, an infrastructure ready to be used as COTS to be installed in any region of the world, which provides about the same accuracy as current RTK systems, both for static and dynamic users, requiring significantly less number of stations, reducing consequently the deployment and maintenance costs
• magicPPP works with a regional network of stations, and is highly flexible for selecting the location of the stations facilitating the possibility of doing precise positioning in remote areas.
• Regional navigation constellations can be used for some PPP purposes, such as scientific applications, demanding high precision but in which the convergence time is not the most stringent requirement
• The use of inter satellite ranging is fundamental for the operation of regional navigation systems, in particular for the precise orbit determination of the satellites in geostationary orbits
References
[1] Laínez Samper, María D., Romay Merino, Miguel M.: OD&TS Process Evolution Based on Interoperability Between Different Navigation Satellite Systems, Proceedings of ION GPS 2009.
[2] Píriz, R., Calle, D., Mozo, A., Navarro, P., Rodríguez, D., Tobías, G., Orbits and Clocks for GLONASS Precise-Point-Positioning, ION GNSS 2009
[3] Laínez, María D. Romay, Miguel M.: Low Cost Navigation Satellite Systems, Coordinates magazine, 2008.
My Coordinates |
EDITORIAL |
|
News |
INDUSTRY | LBS | GPS | GIS | REMOTE SENSING | GALILEO UPDATE |
|
Mark your calendar |
MARCH 2011 TO NOVEMBER 2011 |
Pages: 1 2




















 (7 votes, average: 1.86 out of 5)
(7 votes, average: 1.86 out of 5)




Leave your response!