Modification of the reference frame of Uzbekistan topographic maps based on the GNSS

Development of the local geoid and establishment of national geodetic network is presented in this work. Results of geoidal heights show that WGS84 ellipsoid surface is located above of SK42 geoid

Mirmakhmudov Erkin Associate Professor, Geology and Geography faculty, Department of geodesy and cartography, National University of Uzbekistan, Tashkent, Uzbekistan

Creating of national reference frame is not an easy task because Earth’s crust continuously undergoes various deformations. Repeated geodetic determinations of the positional relationships and elevations of points on the earth’s surface at certain time intervals make it possible to determine the velocity and direction of horizontal and vertical movements of the earth’s crust. Due to tectonic plate motion, different parts of Central Asia move relative to each other with velocities of the order of three centimeters per year. For determination of such a magnitude of motion a GPS technique is used based on WGS84. Geodetic coordinates are always obtained in a system that has been constructed itself using real observations, a geodetic datum: a physical realization of a coordinate system used for describing point locations. The topographic variety of the territory of Uzbekistan imposes complex geodetic measurements and this variety creates a difficulty in developing a national ellipsoid. Crustal deformations and earthquakes within the lithosphere plate of Central Asia have been registered since 1990. In the area of high risk permanent GPS arrays play an increasingly important role. Geodynamic processes in Uzbekistan can also be monitored at stations equipped with GPS receivers. A multilateral cooperation between different geodetic, seismological, and geological institutions in Central Asia and the GeoForschungsZentrum (GFZ) Potsdam started in 1992. Results from repeated measurements across the 90 sites of Central Asian Tectonic Science (CATS) GPS network have provided direct evidence of current high rates of tectonic deformations. These deformations affect the change in the coordinate system of topographic maps as shown in Figure 1. To improve the quality of the topographic maps and monitoring the distortions associated with the local geodetic system, studies are being performed of the GNSS contribution for an overhaul of the State Geodetic System. Today the ‘map’ may be developed by a geographical information system (GIS) but the principle is exactly the same. Map coordinates of points computed from its ellipsoidal latitude and longitude by a standard formula is known as the Gauss-Krüger projection. We need to understand the reasons for the differences, which might arise when comparing these coordinates with those obtained from modern coordinate systems. One of the main tasks is the derivation of representative transformation parameters for two systems. Preliminary transformation parameters between SK42 and WGS84 are determined for two GPS permanent stations and also for some points of CATS network. The coordinate differences are calculated by Molodensky and Helmert methods. The results of these transformations can be used to create a national reference frame of Uzbekistan. The first step is to use an intermediate grid between the two systems. Clear relationships between the Gauss- Krüger and UTM map projections for the Uzbekistan territory are given in this paper.

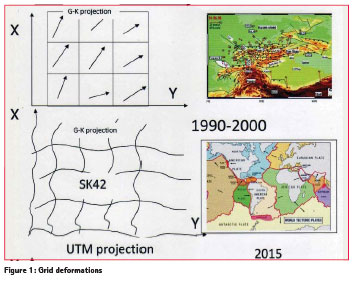
Modification of Gauss- Krüger projection (cylindrical projection)

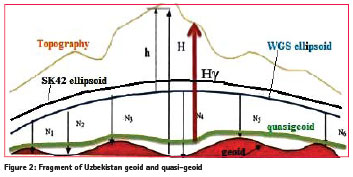
At the beginning of the 19th century, Central Asian triangulations were performed in order to use them as a basis for geographical investigations and topographical maps. The original triangulation was carried out between 1930 and 1950 and is known as the ‘Basic Triangulation’. Before 1940 all geodetic measurement were carried out in the coordinate system, CS32, based on the Bessel ellipsoid. The positions of geodetic control points are determined primarily by the method of triangulation, which is based on the trigonometric principle of measuring distances. The triangulation method consists of establishment on the terrain chains and networks of triangles consecutively interconnected by common sides. The error in measured angles of the triangles in Ist order and IInd order triangulation is usually not more than 0.7’’. The altimetry was carried out with chains of precise leveling. The Uzbek geodetic network was established on the basis of angular and leveling measurements. Classical measurement methods have been mostly replaced by space-based techniques and they are only used today on a local basis or in areas where satellite techniques are not available. The former Soviet Union and Uzbekistan used the SK42 based on the Krasovsky ellipsoid and projection into the Gauss-Krüger coordinate system with six degrees meridian strips. In the towns of the Republic of Uzbekistan as well as in Central Asia the SK63 was used, and is still in use. The rectangular coordinates of the point (points) in the maps of the SK-63 are calculated in the Gauss-Krüger projection, based on the parameters of the Krasovsky ellipsoid, but only at 3° zones. Coordinates (different from the coordinates from maps made in system 1942) are obtained by moving the axial zone of the meridians and replacing the origin of coordinates. The projection is normally made into the Geographic coordinate system or into the Gauss- Krüger coordinate system with six degrees wide meridian strips. Large-scale maps were made using Local Coordinate Systems or the Gauss-Krüger coordinate system with three degrees wide meridian strips. This projection had constant scale along the central meridian and was known as the Gauss conformal projection. Topographic map based on SK42 has geographic coordinates, constant scale Figure 2: Fragment of Uzbekistan geoid and quasi-geoid along the central meridian, rectangular coordinates x,y, in the projection and heights are usually stated to be heights above Baltic sea level (BSL). The published heights of all benchmarks, town survey marks and trigonometric beacons are orthometric heights H above BSL. The orthometric height should never be given without stating the geoid model used. The geoid model allows determine heights using GPS. Different geoid models give different heights for a point, even though the ellipsoid height might be very accurate. Height changes are mainly of interest for engineering purposes or for determination of vertical crustal movements. Vertical crustal movements are also of interest in connection with tide gauges to control sea level rise. The determination of orthometric heights using GPS is a long-term goal in surveying, in order to substitute time consuming and expensive spirit (differential) leveling. However, the SK42 and BSL have become a national standard in Uzbekistan, and are likely to remain a long time. Since 1977 all heights of topographic maps are normal heights Hγ, which were calculated relative to the quasigeoid (Figure 2).

Geoid height (N) is the height of the geoid above ellipsoid and it depends on latitude and longitude. Ellipsoidal height (h) is the height of the Earth’s surface above the ellipsoid. The relationship between orthometric height (H) and ellipsoidal height (N) is given by H = h – N. Reduction of the normal height Hγ to the ellipsoidal height h is necessary to calculate the Gauss- Krüger Cartesian coordinates in the case of seven transformation parameters determination. Transformation parameters are determined by using these Cartesian coordinates and the WGS84 geocentric coordinates of the identical points.

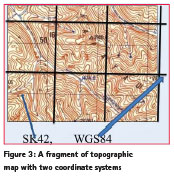
At the initial stage it is planned to use an additional grid based on the WGS84. Additional reference frame based on modified Gauss – Krüger projection is more suitable for topographic maps in scales 1:100000-1:10000. A fragment of topographic map with two coordinate systems is shown below (Figure 3). The transition into the additional reference frame will help the surveyors and geodesists to use the classical and modern coordinates which are based on the two ellipsoids.

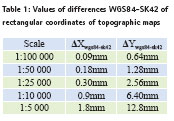
Table 1 shows the increase in values of the differences WGS84-SK42 of rectangular coordinates of topographic maps in scales from 1:100000 to 1:5000. Therefore, the surveyor can use both coordinates, depending on the task. These maps will temporarily be used because the digital maps of Uzbekistan are very expensive. In the future we need to develop a new digital map which will be more suitable for Uzbekistan.

One of the most significant developments of the past few years has been the establishment of the International GPS Service for Geodynamics. CATS project has a wider scope and covers the Central Asian region. Coverage area of GPS stations of Uzbekistan is not yet optimal. It is planned to further extend the CATS network. This starting configuration will be augmented by additional GPS stations in those areas where nothing exists, in order to obtain a more or less homogeneous data. Use of GPS will help for more correctly determination of the local geoid. In this study some data of the CATS program are used for computing of a geoid-ellipsoid separation. The geoidal heights were calculated for 15 CATS points (Table 2).

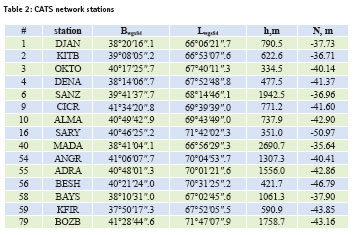
Transformation between SK42 and WGS84

The coordinates derived by GPS are referred to a global and reference frame. In order to reduce these coordinates to a local (national) coordinate frame a transformation must be performed. Converting consists of derivation of representative transformation parameters for two systems. This transformation may be performed in two steps. The first step is transformation of any kind of map projection systems to the SK42 ellipsoidal coordinates, and then from the SK42 ellipsoidal coordinates into the WGS84. There are formulas for calculating changes between geodetic datum if the point positions are expressed as latitude and longitude coordinates, without first converting the positions into Cartesian coordinates. The formulae cannot cope with a difference in orientation of the ellipsoid axes – it only deals with a translation of the origin and changes in ellipsoid size and shape. This transformation is one of the most widely used techniques for transforming geodetic coordinates from one system to another. It is also one of the least accurate, due to the fact that it does not account for rotation or scaling between two systems. The equation between SK42 and WGS84 is given by:

Bsk42=Bwgs84+ΔB

Lsk42=Lwgs84+ΔL (1)

Hsk42=Hwgs84+ΔH

The usual mathematical form of the transformation is a linear formula which assumes that the rotation parameters are ‘small’. Rotation parameters between geodetic Cartesian systems are usually less than 5 seconds of arc, because the axes are conventionally aligned to the Greenwich Meridian and the Pole. Transforming local coordinates to WGS 84 does not improve the accuracy of the transformed coordinates. In fact, transformed geodetic coordinates will be less accurate because the errors in the transformation are added to the errors in the original local coordinate system.

In general, two three-dimensional coordinate systems in space are related to each other by the following equations:

where, Δx is translation along the X-axis, Δy is translation along the Y-axis, Δz is translation along the Z-axis, ωx- rotation about the X-axis, ωy- rotation about the Y-axis, ωz rotation about the Z-axis, μ- scale factor.

Results from the calculation of the differences between two coordinate systems are given in the Table 3.

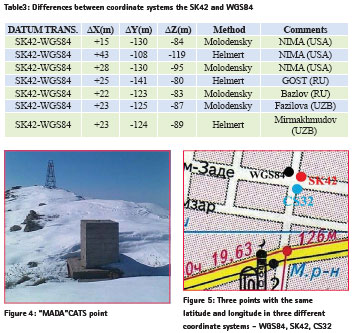
The values of the transformation parameters ΔX, ΔY, ΔZ between the two systems are similar to each other, although the two methods of transformation have been used. Even if we are going to use the same transformation method, the differences are due to different geodetic networks, software and the accuracy of the coordinates of the initial geodetic points. Positioning errors can be introduced from a variety of geodetic sources, dramatically influencing the success of a drilling program. To determine the transformation parameters between WGS84 and SK42 we used some CATS network points (Figure 4.) The quality of the network geometry of the CATS network is in the order of 1-3mm for horizontal components and about 5 mm for the height. This is derived from Helmert transformation between the daily solutions and the campaign solution. The global network accuracy is in the order of 1-2cm. Difference of a coordinates between two systems (Δλ= 3,26//, Δφ=-0,17//,Δh=108,84m, ΔX=+23 m, ΔY=-124 m, ΔZ=-89 m) and velocity of Kitab station (31 mm/yr) were calculated taken into account local conditions. These results are close to the values obtained from the optic observations ( , which were carried out by visual zenith-telescope in 1930- 1978. These velocities are secular motion in latitude and longitude due to plate tectonics (AMO-2 model) in 10-4 ‘’/cy and 10-5 s/cy. For the best transformation model and reducing the fit errors, it is need to use data from satellite laser ranging. Transformation between SK42 and WGS84 typically is not recommended for most applications because standard transformations can introduce error that is larger relative to their difference (Figure 5). Complicating the matter, the difference between SK42 and WGS84 varies with time and location. Both systems have frequent new realizations due to more data and improved techniques.

The figure 5 shows three points which all have the same latitude and longitude but in three different coordinate systems (SK42, WGS84 and CS32) on Khakim- Zade and Bodomzor streets in the city of Tashkent . Each one of these coordinate systems is widely used in Uzbekistan and fits for its purpose, and none of them is wrong. The differences between them are just a result of the fact that any system of ‘absolute coordinates’ is always arbitrary. Usually the town surveying is produced in the local coordinate system, which has definitely been referred to the state geodetic network. SK63 (Krasovsky spheroid) is used for topographic works of big cities. In the maps of the coordinate system 1963 (SK-63) rectangular coordinates of the point (points) are calculated in Gauss – Krüger projection, based on the parameters of the Krasovsky ellipsoid, but only at 3° zones. Coordinates (different from the coordinates from maps made in system 1942) are obtained by moving the axial zone of the meridians and replacing the origin of coordinates.

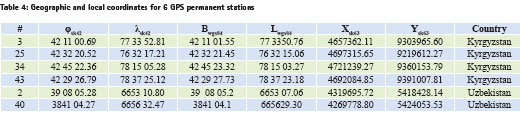
There is software for converting between two coordinate systems. But these computer programs were created on the basic approximate equations and they can be used for testing of a geographical coordinates, as well. For 6 GPS permanent stations were calculated the local geodetic coordinates at the Tashkent State Technical University (Table 4).

GNSS network of Uzbekistan

GNSS is widely used in Uzbekistan for many purposes, but more global and fundamental is mapping of a land. GNSS use in mapping can be divided into three sections: education, research and practical application. The main and important is the practical use for the construction of high-precision geodetic network and seismology. The whole territory of Uzbekistan was covered with the state geodetic network taking into account the scale, orders and a configuration. Usually, it is necessary to make a preliminary calculation of the accuracy of the network points if we are going to design a geodetic network. However, the satellite geodetic network of Uzbekistan is created on the basis of a practical experience of mapping agency workers. The state geodetic network of Uzbekistan was divided into orders – I, II, III, and IV depending on accuracy and methods of surveying. The positions of geodetic control points are determined primarily by the method of triangulation, which is based on the trigonometric principle of measuring distances. Geodetic points are located on elevated points of the terrain and are selected by reconnaissance. Each point is marked on the terrain by laying concrete block at a certain depth with a mark on it that designates the apex of the triangle and monumentation of a wooden or metal tower that serves as a stand for the angular measuring instrument and as a sighting target (geodetic target) when measuring angles. Sometimes geodetic points combined with prominent local objects, such as water towers and steeples of tall building. Geodetic networks are subdivided into orders, depending on the sequence of construction and precision of measurements. Now, some geodetic targets of the state geodetic network of Uzbekistan are lost or are out of order. In order to renovate these targets, benchmarks and geodetic points it is necessary some financial support. But the use of GPS is the most effective and accurate when mapping the territory of the Republic of Uzbekistan.

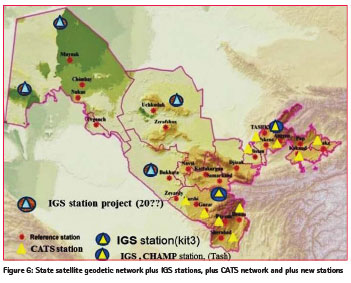
In 2002 the state satellite geodetic network was designed including Kitab and Tashkent GPS stations and 16 first order basic stations by mapping agency of Uzbekistan (Figure 6). There were produced GPS measurements with help of GNSS technologies and calculated preliminary space coordinates based on the WGS84. Due to the lack of a geodetic network computing software the adjustment is not performed. . It is planned that this network will have International Terrestrial Reference Frame (ITRF) based on the national reference system. Since the 1990s Kitab station hosted the GPS reference station (KIT3), included in International GNSS Service (IGS) and ground based beacon of DORIS satellite tracking systems, providing IERS data center with precise coordinates at sub daily frequency. Due to the dense and homogeneous global beacon network DORIS significantly contributes to the realization and maintenance of the ITRS.

The CATS network was observed during five GPS campaigns in the years 1992, 1994, 1995, 1996, and 1998. The processing software EPOS was used to derive coordinates and site velocities. The network solutions were tied to the International Terrestrial Reference Frame (ITRF97). Campaign data were processed simultaneously with data from globally distributed IGS and permanent GFZ stations in Central Asia.

The analysis of Uzbek CATS network shows that from 1992 to 1998 all station latitudes and longitudes of this network are changed with a constant rate of about 2.5 cm/yr in northeast. Over the course of a decade or so, this effect may become noticeable in large-scale mapping.

Conclusion

Development of the local geoid and establishment of national geodetic network is presented in this work. Results of geoidal heights show that WGS84 ellipsoid surface is located above of SK42 geoid. The transition to the additional reference frame will help the surveyors and geodesists to use modern coordinates, which are based on the two ellipsoids. The results of transformed coordinates will be the basis for establishment of a national geodetic network. Data of Kitab, Tashkent and Maydanak observatories will be used for investigation the kinematic parameters of reference points and for improvement of transformation parameters between the two reference systems. It will be accurately measured and modeled the geoid and its gravity field precisely to determine the position and velocity of points or objects at the surface. The combination of GNSS and classic geodetic measurements lead to geometric methods of solving this problem. Modernization of the satellite geodetic network will improve the network of Uzbekistan. For this purpose the following problems must be solved:

– Establishment of fundamental geodetic control,

– Densification of existing geodetic control,

– Analysis and improvement of existing geodetic control, and

– Contribution to geoid determination.

Acknowledgements

The author thanks Prof K Vassileva for useful advice.

References

Gauss C.F.(1825) Allgemeine Auflosung der Aufgabe, die Teile einer gegenbenen Flache so abzubilden, dass die Abbildung dem Abgebildeten in den kleinsten Teilen ahnlich wird.

Gunter Seeber.(2003) Satellite Geodesy. New York.

Helmert, F. R. (1962) Die mathematischen und physikalischen The orien der höheren Geodäsie, 2nd ed. vols. 1-2. Leipzig.

Hofmann-Wellenhof B., Lichtenegger H., Collins J.(2001) Global Positioning System: Theory and Practice. 6th ed., Springer-Verlag, Wien-New York.

Krasovsky F. N. (1942) Rukovodstvo po vysshei geodezii, part 2. Moscow. (in Russianrus).

KrugerKrüger L.(1912) Konforme Abbildung des Erdellipsoids in der Ebene, Veroff. Des K. Peuss. Geodat. Institutes, neue Folge, #52, Verl. Von B.G. Teubner, Lpz.

Mirmakhmudov E., Safarov E., Fazilova D. (2012) Modification of vertical reference frame. Abstract.United Nations/Riga /United States of America Workshop on the Applications of GNSS, Latvia, Riga, 14 -18, May.

Moritz H. (2000) Geodetic Reference System 1980. J. Geod.74: 128–133.

Reigber Ch. et al.(1999) GPS constraints on the distribution of deformation of the Tien Shan, N-Pamirs and behavior of the Tarim, 14th Himalaya-Karakorum- Tibet Workshop, Terra Nostra, 127.

Vondrak J. (1991) Calculation of the series of the Earth orientation parameters in the Hipparcos reference frame. Bulletin of the Astronomical Institutes of Czechoslovakia. Praha.Vol.42, №.5. P.283-294.

Zubovich, A. V., et al.(2010) GPS velocity field for the Tien Shan and surrounding regions, Tectonics,29, TC6014, doi:10.1029/2010TC002772

http://www.unoosa.org/pdf/sap/2011/ UAE/Presentations/30.pdf http://www.unoosa.org/pdf/sap/2013/ croatia/Abstracts_Croatia2013.pdf