| Positioning | |
Flight evaluation of a ‘GADA’
The development and the evaluation of GPS attitude determination algorithm (GADA)’s static and dynamic characteristics are presented and the results are considered satisfactory for the application. |
|
For the final evaluation of a GPS attitude determination algorithm (GADA), it was determined its true performance in terms of its accuracy, reliability and dynamic response. To accomplish that, a flight test campaign was carried out at the Brazilian Flight Test Division (GEEV) to validate the attitude determination algorithm. In this phase, the measured aircraft attitude was compared to a reference attitude, to allow the determination of the errors. The flight test campaign was carried out at the Brazilian’s Flight Test Division T-25C 1956 Basic Trainer aircraft manufactured by EMBRAER. The performance and accuracy of the system is demonstrated under static and dynamics tests profiles, which are fully compliant with the Federal Aviation Administration (FAA) Advisory Circular (AC) 25-7A. Dynamic response of the system is evaluated. Data reduction analysis of more than 12 hours flights showed that GADA errors are satisfactory for attitude determination. Also it is presented that its static accuracy is highly dependable of the Attitude Dilution of Precision (ADOP) while the dynamic accuracy depends upon the GPS receiver PLL model and coefficients
Introduction
The aircraft attitude is the angular relationship between the aircraft body reference system SB and the Earthfixed reference system SR, expressed by the Euler angles: θ (pitch), φ (roll), and ψ (yaw). Using three sequential rotations over the Euler angles in the following sequence: [ψ θ φ] it is possible to express the transformation matrix [1], from SR to SB as:
Where: cθ ≡ cos(θ); sθ ≡
sin(θ); cφ ≡ cos(φ); sφ ≡ sin(φ);
cψ ≡ cos(ψ); and sψ ≡ sin(ψ).
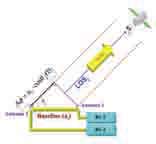
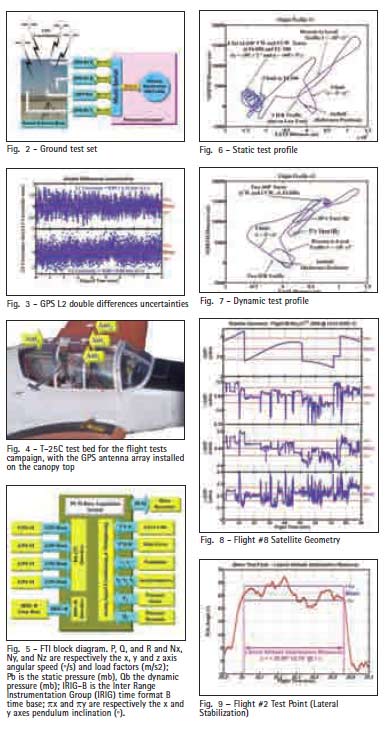
Fig. 1 – GPS Interferometry
The basic measurement for GPS attitude determination is the phase difference (Δφ) between the signals received by two
antennas that define a baseline (Fig.1), as:
Where: ai = is the ith baseline length, θj = is the angle between the baseline ai and the line of sight to the jth GPS Satellite Vehicle (SVj).
The GPS attitude determination algorithm uses two baselines (a1 , a2) plus a computed baseline (a3) to define a Cartesian coordinate system SG. The SG axes (xG, yG, zG) are fixed on the aircraft body, and defined by the placement of three antennas (Ant1; Ant2 and Ant3) [2].
Given an aircraft attitude, it is possible to express the relationship between siR, a unit vector in the direction of SVi in SR, and Bjj, the projection of siR on the baseline aj [3], as:
Considering that there may be errors in the measured Euler angles, eq.3 is not fully satisfied. So a known published solution (i.e. REQUEST algorithm) [4] defines a cost function (ρ), which depends on the transformation matrix (LGR):
Where: k is a given coefficient, n is the number of SV being tracked, and pi is a fixed weight value attributed to SVi.
The attitude determination algorithm, using least-square fit techniques, searches for the transformation matrix LGR that minimizes ?.
Several algorithms (e.g REQUEST)
have been developed to solve this problem [6], where the estimation of the z-axis is given by:
GPS attitude determination
To avoid undesirable perturbations, a GPS receiver does not track the signal from a SV when its Elevation Angle (EL) is below a certain angle (e.g., EL < 15º). When the aircraft is maneuvering, the Line of Sight Angle (LOS) of a given SV (considering EL > 15º), could be momentarily below the GPS Horizontal Antenna Plane (HAP). In this case, the true value of the single difference measurement is given by choosing the negative value of eq. 7.
The use of the positive roots of eq. 7 at the above condition results in a divergent solution, rendering this algorithm unreliable for all flight conditions.
In fact Ground Based Augmentation System (GBAS) applications [8] and [9], report that an airborne GPS receiver is capable of tracking signals from Pseudolites (PL), using only a top mounted antenna.
Therefore a new GPS Attitude Determination Algorithm (GADA) was developed [10] and compared against REQUEST. The main difference between both algorithms is the fact that REQUEST uses the positive value of eq.7, while GADA searches for its true signal.
The GADA development comprised three phases:
1) Simulation;
2) Ground Tests; and
3) Flight Test.
The simulation process was developed with Matlab® 6.1 with the Satnav® Toolbox and used the REQUEST algorithm as a reference for cross evaluation. The resulting REQUEST errors were ±3.463º
in θ, ±4.891º in φ, and ±3.513º in ψ while the GADA errors were, respectively, ±0.179º, ±0.199º, and ±0.131º, at 1σ.
The ground tests were a preview of the real flight environment and provided data to certify that the algorithm works properly. Then a swivel base for the antennas was designed and a data acquisition system was integrated (Fig. 2).
So it was possible to measure the double differences uncertainties
(Fig. 3) and to evaluate the attitude of the swivel antenna base.
The Flight Tests Campaign was carried out with the Universal Trainer T-25C 1956 (Fig. 4). To allow redundancy, an additional baseline (i.e -y-axis, Ant4) was merged to the antenna array (Fig 4).
Along with the GPS receivers, it was integrated a Flight Tests Instrumentation System (FTI) which provided attitude reference and flight dynamics parameters (Fig.5).
The uncertainties of all FTI parameters were determined using SALEV® system [11] that is fully compliant with EA-4/02 Standard [12].
The correlation of the aircraft attitude solutions provided by both FTI and GADA requires:
1. Time synchronization of all observables [13] provided by the
FTI and the GPS receivers; and
2. The determination of the misalignment angles [14] between all reference systems:
The Flight Tests Campaign was carefully planned to best characterize GADA’s performance. To accomplish it was designed two tests profiles. The first profile (Fig. 6) was aimed for static attitude determination where semi-static attitudes maneuvers were
employed to check the system capability to determine the correct attitude.
The second profile (Fig. 7) employed dynamic maneuvers to check the system response.
In total it was executed 11 flights, 2 for FTI shakedown, 5 with the static profile and the remaining 4 with the dynamic profile, totaling almost 12 flight hours.
To improve the statistical analysis, all flights were scheduled accordingly to keep a uniform Geometric Dilution of Precision (DOP) factor [15].
Fig. 13 – ψ Attitude error during the Lateral Attitude Stabilization Maneuver Fig. 14 – The Longitudinal Attitude Capture Maneuver
In fact the measured DOP for all fights was 3.05 ± 0.274 @ 1σ, and the resulting Attitude Dilution of Precision (ADOP) components [16] for θ, φ and ψ were respectively 0.454 ± 0.035; 0.447 ±
0.022 and 0.239 ± 0.031 @ 1σ.
As reference Fig. 8 depicts the DOP and the ADOP components of flight #8 on may 21st, 2004 at 13:33 Greenwich Mean Time (GMT).
|
||||||||||||||||||||
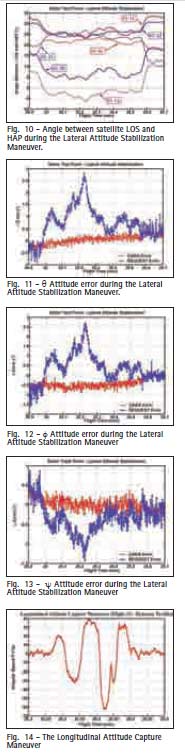
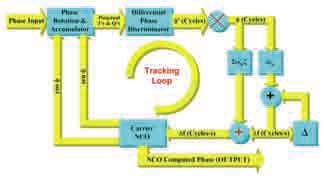
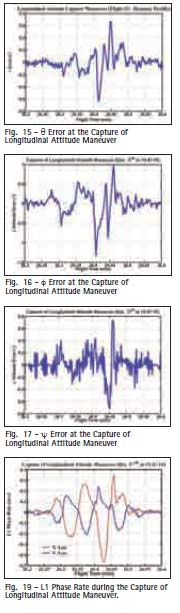
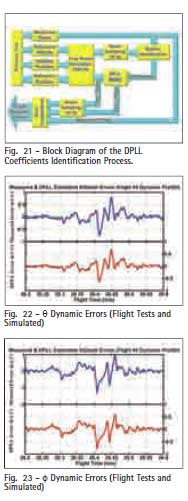
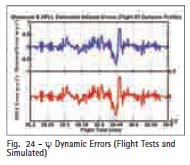
Flight Tests resultsStatic PointsIn all static tests points GADA’s performance was satisfactory. As example for the lateral attitude stabilization maneuver with f = +25.86º ± 2.76º @1s (Fig. 9), it is possible to verify that SV #14 LOS were mostly bellow HAP (Fig. 10). As results it is also possible to verify that in this flight condition GADA kept its accuracy while REQUEST diverged (Fig. 11 to 13). Dynamic PointsThe analysis of the dynamic maneuvers it was noticed that GADA’s errors increased with the angular speed. When the aircraft is performing the capture of the longitudinal attitude maneuver (Fig. 14) with a roll rate ?±55º/s, it is possible to notice the error build up between the FTI reference attitude and the GADA’s computed attitude (Fig. 15 to 17). Dynamic error analysisThe functional analysis of the Phase Locked Loop – PLL (Fig. 18) of a GPS receiver [17], could explain these dynamic errors (Fig. 15 to 17). When the aircraft is maneuvering, the rate of change of the Doppler shift may result in a difference between the real phase (i.e. the input at the PLL) and the corresponding NCO phase measurement (i.e. output measurement). Considering the topology presented Fig. 11 – ? Attitude error during the Lateral Attitude Stabilization Maneuver. Fig. 12 – f Attitude error during the Lateral Attitude Stabilization Maneuver Fig. 10 – Angle between satellite LOS and HAP during the Lateral Attitude Stabilization Maneuver. 28 | May 2009 in fig. 18, the transfer function of the PLL is expressed by: Where: ? is the damping factor (adm); and ?N is the natural frequency (rd/s). In dynamic conditions there is a phase delay error between the true phase (i.e. what we want to measure) and the NCO generated phase (i.e. the resulting measurement provided by the receiver). The capture of the longitudinal attitude maneuver increases the phase rate (Fig. 19) and the associated phase error. To investigate this effect it would be necessary to: 1. Simulate the same flight condition in order to get the true phase measurement; 2. Apply the simulated phase to the receiver PLL model; 3. To compute GADA attitude solution with the PLL resulting phase; and 4. To compare the resulting GADA attitudes (i.e. Simulated and the flight tests ones). But the true characteristics of a commercial off the shelf GPS receiver PLL is proprietary and the manufacturer does not disclosures such information. So alternatively it was employed a system identification process (Fig. 21) to best estimate the PLL coefficients and topology for each GPS receiver. Then it was possible to compare the dynamic errors measured at the flight tests campaign with the simulated errors. The resulting analysis presents an acceptable DPLL modeling (Fig. 22 to 24). ConclusionsThe development and the evaluation of GADA’s static and dynamic characteristics are presented and the results are considered satisfactory for the application. The results show that GADA’s accuracy is dependent of the receiver DPLL characteristics. Future works should use a software GPS receiver, where the setup of the DPLL coefficients and topology, allows: 1) The validation of the dynamic behavior of an off-theshelf GPS receiver; and 2) The design of customized GPS receivers, for specific high dynamics applications. Also GADA should be evaluated in other test beds, that flies over an extended envelope and thus in a higher dynamic range. AcknowledgmentsWe wish to thank the partial support given by the Flight Test Group, for supporting the measurement and the flight tests campaigns. Also we like to tank FINEP under agreement 01.07.0663.00 and 01.07.0540.00 that respectively funded the telemetry system used for the flight tests campaign and its spares parts. Fig. 18 – GPS receiver phase tracking loop block diagram Reference:[1] ETKIN, B. Dynamics of Atmospheric Flight. New York:John Willey & Sons, 1972. [2] COHEN, C. E. Attitude Determination. In: AIAA. Global Positioning System: Theory and Applications. Washington: AIAA, 1996, v.2, cap.19, p. 519-537. [3] Shuster, M. D.; Oh, S. D. Threeaxis Attitude Determination from Vector Observations. IEEE Journal of Guidance and Control, Washington, v. 4, n.1, p. 70-77, 1981. [4] BAR-ITZHACK, I., Y. REQUEST: A Recursive Quest Algorithm for Sequential Attitude Determination. IEEE Journal of Guidance and Control and Dynamics, Washington, v.19, n.5, p. 1034-1038, 1996. [5] STEVENS, B. L., and LEWIS, F. L., Aircraft Control and Simulation,2nd ed. Hoboken, NJ: John Wiley& Sons, Inc. 2003, ch. 1.3. [6] BAR-ITZHACK, I, Y; Y. MONTGOMERY, Y; and GARRICK J. C., Algorithms for Attitude Determination using the Global Positioning System, IEEE Journal of Guidance and Control and Dynamics, vol. 21, nº 6, pp. 846–852, 1998. [7] BALANIS, C. A. Antenna Theory Analysis and Design. New Jersey: John Willey & Sons, 2005, 3rd ed., cap. 2.2, p. 33-38. [8] ELROD. B. D; BALTROP. K; DIERENDOCK. V. A. J. Testing GPS Augmented with Pseudolites for Precision Approach Applications. In: Institute of Navigation National Technical Meeting of the Satellite Division (ION-GPS), 1994, Salt Lake, Proceedings … Salt Lake: ION-GPS, 1994. p. 1269-1278. [9] ELROD B. D; DIERENDONK. V. A. J. Pseudolites. In: AIAA. Global Positioning System: Theory and Applications. Washington: AIAA, 1996, v.2, cap.2, p. 51-79. [10] Leite, N. P. O; Walter, F. The Development and Simulation Results of a GPS Attitude Determination System. In: Institute of Navigation National Technical Meeting of the Satellite Division (ION-GPS), 2002, Portland. Proceedings … Portland: ION-GPS, 2002. p. 1100-1107. [11] SOUSA, L. B. R.; Leite, N. P. O.; CUNHA, W. C.; and Walter, F. Automation System for the Flight Test Laboratory (SALEV). In: International Telemetering Conference (ITC/USA), 2006, SanDiego. Proceedings … San Diego: ITC/USA, 2006. p. 94-103. [13] Leite, N. P. O.; Walter, F. Multiple Time Base Synchronization Process Applied to the Flight Tests Campaign of a GPS Attitude Determination Algorithm. In: International Telemetering Conference (ITC/USA), 2007, Las Vegas. Proceedings … Las Vegas: ITC/USA, 2007. p. 1048-1057. [14] Leite, N. P. O.; Walter, F. The Development of an Alignment Process to be Used on Flight Test Campaign of a GPS Attitude Determination System. In: Institute of Navigation National Technical Meeting (ION-NTM), 2003, Anaheim. Proceedings … Anaheim: ION-NTM, 2003. p. 152-162. [15] SPILKER, J. J. Satellite Constellation and Geometric Dilution of Precision. In: AIAA. Global Positioning System: Theory and Applications. Washington: AIAA, 1996, v.1, cap.5, p. 177-208. [16] Yoon, S; Lundberg, J. B. Euler Angle Dilution of Precision in GPS Attitude Determination. IEEE Transactions on Aerospace and Electronic Systems, New York, v. 37, n.03, p. 1077-1083, 2001. [17] DIERENDOCK. V. A. J. GPS Receivers. In: AIAA. Global Positioning System: Theory and Applications. Washington: AIAA, 1996, v.1, cap.8, p. 329-407. |
||||||||||||||||||||
|
||||||||||||||||||||
|
Pages: 1 2

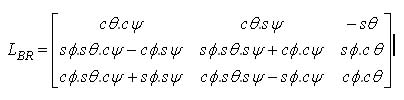
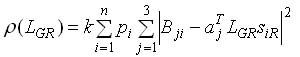
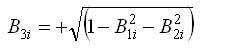
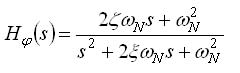













 (1 votes, average: 1.00 out of 5)
(1 votes, average: 1.00 out of 5)



